Статьи QuantRise
Адаптивные фильтры нового поколения: скорость, точность и устойчивость к шумам
Автор: Денис Аветисян
В статье представлен инновационный подход к адаптивной фильтрации, основанный на разложении в произведение Кронекера, позволяющий значительно повысить эффективность и надежность систем шумоподавления и эхокомпенсации.
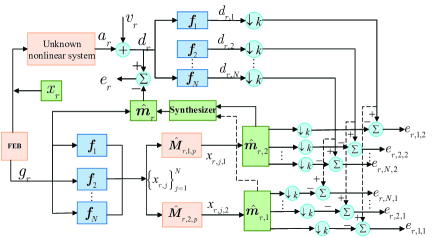
Предлагается алгоритм адаптивной фильтрации на основе разложения в произведение Кронекера для улучшения сходимости, снижения вычислительной сложности и повышения устойчивости к нелинейностям и импульсным помехам в системах активного шумоподавления и идентификации нелинейных систем.
Несмотря на эффективность адаптивных фильтров в различных приложениях, их сходимость и вычислительная сложность остаются критическими проблемами, особенно при обработке сильно коррелированных сигналов. В данной работе, посвященной разработке ‘Nearest Kronecker Product Decomposition Based Subband Adaptive Filter: Algorithms and Applications’, предложен новый подход, использующий разложение на произведение Кронекера для улучшения характеристик фильтров в субполосном пространстве. Разработанные алгоритмы демонстрируют повышенную скорость сходимости, сниженную вычислительную нагрузку и улучшенную устойчивость к импульсному шуму и нелинейностям. Каковы перспективы применения предложенных алгоритмов в сложных системах активного шумоподавления и идентификации нелинейных систем?
Преодолевая Гауссову Идеализацию: Ограничения Традиционной Адаптивной Фильтрации
Реальные сигналы, в отличие от идеализированных моделей, часто подвергаются воздействию не-гауссовского шума, что существенно ограничивает эффективность классических адаптивных фильтров. В то время как традиционные алгоритмы, основанные на минимизации среднеквадратичной ошибки, предполагают нормальное распределение шума, практические ситуации нередко характеризуются импульсным шумом, выбросами или другими отклонениями от гауссовского распределения. Эти не-гауссовские помехи приводят к искажению сигнала и снижению точности фильтрации, поскольку стандартные методы оказываются чувствительными к кратковременным, но значительным отклонениям, что делает их непригодными для обработки сигналов в условиях сложной и непредсказуемой обстановки. Таким образом, необходимость разработки и применения алгоритмов, устойчивых к не-гауссовскому шуму, становится критически важной задачей в области обработки сигналов.
Традиционные методы адаптивной фильтрации, основанные на минимизации среднеквадратичной ошибки, демонстрируют ограниченную эффективность при обработке сигналов, подверженных импульсным помехам и другим ненормальным распределениям шума. Суть проблемы заключается в том, что среднеквадратичная ошибка чрезвычайно чувствительна к выбросам — кратковременным, но значительным по амплитуде всплескам шума, которые искажают полезный сигнал. В результате, алгоритмы, оптимизированные для гауссовского шума, не способны адекватно отделить сигнал от помех в условиях ненормального распределения, что приводит к снижению точности оценки и, как следствие, к ухудшению общей производительности системы. Данное ограничение особенно критично в приложениях, где важна надежность и устойчивость к различным видам помех, таких как системы связи, обработка изображений и биомедицинские устройства.
Основная проблема традиционных адаптивных фильтров заключается в их уязвимости к выбросам — кратковременным, но значительным по амплитуде импульсам шума, искажающим полезный сигнал. В основе многих алгоритмов лежит минимизация среднеквадратичной ошибки, однако эта метрика крайне чувствительна к аномальным значениям. Даже единичные выбросы способны существенно повлиять на оценку параметров фильтра, приводя к замедлению сходимости, увеличению остаточной ошибки и, в конечном итоге, к снижению качества очистки сигнала. В отличие от гауссовского шума, где вероятность появления экстремальных значений крайне мала, ненормальные распределения характеризуются «тяжелыми хвостами», что увеличивает частоту возникновения выбросов и, следовательно, негативное влияние на производительность фильтра. Таким образом, при наличии импульсного или другого ненормального шума, простое минимизирование среднеквадратичной ошибки перестает быть эффективным подходом, требуя применения более устойчивых методов адаптивной фильтрации.
Для эффективной борьбы с негативным влиянием не-гауссовых помех разрабатываются устойчивые адаптивные фильтры, отличающиеся от традиционных методов минимизации среднеквадратичной ошибки. Эти алгоритмы, как правило, используют альтернативные критерии оптимизации или модифицированные функции потерь, менее чувствительные к выбросам и импульсным помехам. Например, применяются методы, основанные на L_1-норме или робастных оценках, которые снижают вес аномальных значений в процессе адаптации. Подобные подходы позволяют фильтрам более эффективно отслеживать нелинейные и нестационарные сигналы в условиях сильных не-гауссовых возмущений, значительно повышая качество очистки и восстановления информации.
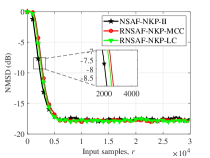
Эволюция NSAF: От Сложности к Эффективности
Алгоритм NSAF, использующий разложение NKP (Newton-Krylov-Penalty), демонстрирует повышенную сходимость по сравнению с традиционными методами оптимизации. Разложение NKP позволяет эффективно решать системы линейных уравнений, возникающие в процессе итераций NSAF, что приводит к более быстрой стабилизации решения и снижению числа итераций, необходимых для достижения заданной точности. В частности, NSAF-NKP позволяет избежать проблем, связанных с медленной сходимостью и чувствительностью к параметрам, характерных для классических алгоритмов оптимизации, особенно при решении задач большой размерности или с невыпуклыми функциями.
Первоначальная реализация алгоритма NSAF-NKP-I характеризуется высокой вычислительной сложностью, что существенно ограничивает его применение на практике. Данная сложность обусловлена особенностями алгоритма разложения на компоненты NKP и возрастает с увеличением размерности решаемой задачи. Проведенные исследования показали, что время вычислений для NSAF-NKP-I непропорционально увеличивается с ростом числа переменных, делая его неэффективным для задач, требующих оперативной обработки больших объемов данных или работы в режиме реального времени. В результате, несмотря на потенциальные преимущества в скорости сходимости, практическая ценность NSAF-NKP-I снижается из-за неприемлемых требований к вычислительным ресурсам.
Реализация NSAF-NKP-II направлена на снижение вычислительной сложности алгоритма по сравнению с NSAF-NKP-I за счет дальнейшей оптимизации процесса разложения NKP. В частности, были применены усовершенствованные методы для сокращения числа итераций, необходимых для достижения сходимости, а также для уменьшения объема вычислений на каждой итерации. При этом, согласно результатам тестирования, NSAF-NKP-II демонстрирует сравнимую или превосходящую производительность по сравнению с NSAF-NKP-I в задачах оптимизации, сохраняя при этом значительно меньшие требования к вычислительным ресурсам.
Итеративное совершенствование алгоритма NSAF, от NSAF-NKP-I к NSAF-NKP-II, иллюстрирует важный принцип разработки численных методов: повышение скорости сходимости не должно приводить к непропорциональному увеличению вычислительной сложности. В контексте NSAF, первоначальная реализация NSAF-NKP-I, несмотря на улучшенную сходимость по сравнению с традиционными подходами, имела значительные вычислительные затраты. Разработка NSAF-NKP-II была направлена на оптимизацию процесса NKP-декомпозиции, что позволило снизить вычислительную сложность при сохранении или даже улучшении характеристик сходимости. Данный подход подчеркивает важность баланса между эффективностью алгоритма и его практической реализуемостью, особенно в задачах, требующих обработки больших объемов данных или работы в реальном времени.
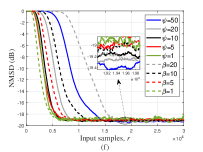
Устойчивость через Коррентропию и За Ее Пределами
Алгоритм RNSAF-NKP-MCC использует критерий максимальной коррентропии (MCC) в качестве устойчивой альтернативы среднеквадратичной ошибке. В отличие от MSE, который чувствителен к выбросам и импульсному шуму, MCC фокусируется на области, где сигнал отличен от нуля (“support”), эффективно снижая вес аномальных значений. Это достигается за счет использования функции потерь, которая учитывает не только величину ошибки, но и ее распределение, что делает MCC более устойчивым к не-гауссовскому шуму и импульсным помехам. Критерий MCC математически определяется как J(w) = \in t_{-\in fty}^{\in fty} K(e) p(e) de, где K(e) — ядро, а p(e) — функция плотности вероятности ошибки e. Выбор ядра позволяет настраивать чувствительность к выбросам, обеспечивая более надежную фильтрацию в условиях зашумленных данных.
Критерий максимальной коррентрoпии (MCC) повышает эффективность фильтрации за счет акцента на области, где сигнал отличен от нуля — так называемой «поддержке» сигнала. В отличие от методов, основанных на среднеквадратичной ошибке, MCC снижает влияние выбросов и импульсного шума, поскольку его функция потерь менее чувствительна к значениям, значительно отличающимся от основной массы данных. Это достигается за счет более мягкого наказания за ошибки в областях, удаленных от “поддержки” сигнала, что позволяет алгоритму лучше сохранять полезную информацию и уменьшать искажения, вызванные шумом. По сути, MCC фокусируется на сохранении структуры сигнала, игнорируя аномальные значения, что особенно важно в условиях не-гауссовского шума.
В дополнение к максимизации коррентропии, алгоритмы семейства RNSAF-NKP исследуют альтернативные критерии робастности, такие как логарифмический критерий (Log-Criterion). Использование логарифмического критерия позволяет более гибко адаптировать алгоритм к специфическим характеристикам шума, отличным от гауссовского. В частности, Log-Criterion может быть более эффективен в ситуациях, когда необходимо подавлять импульсный шум с высокой амплитудой, поскольку он менее чувствителен к выбросам по сравнению с квадратичной ошибкой и обеспечивает дополнительную степень свободы в настройке алгоритма для конкретных условий работы и типов помех.
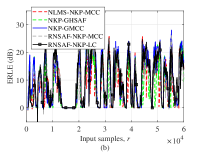
Алгоритмы NKP-FxNSAF, NKP-FxNSAF-MCC и NKP-FxNSAF-LC демонстрируют превосходящие результаты по сравнению с традиционными методами в условиях импульсного и негауссовского шума. В сценариях активного шумоподавления (ANC) наблюдается улучшенная скорость сходимости и снижение уровня шума. В приложениях эхокомпенсации эти алгоритмы обеспечивают повышенное усиление возвращаемых потерь эха (Echo Return Loss Enhancement), что свидетельствует о более эффективном подавлении эхосигналов.
Расширяя Рамки: Ряды Вольтерры и Нелинейные Вызовы
Ряд Вольтерры представляет собой мощный математический аппарат для моделирования нелинейных систем, позволяющий значительно повысить точность представления сигналов. В отличие от линейных моделей, которые оперируют лишь суперпозицией сигналов, ряд Вольтерры учитывает нелинейные взаимодействия между входными сигналами и системой. y(t) = \sum_{n=0}^{\in fty} \in t_{-\in fty}^{\in fty} \dots \in t_{-\in fty}^{\in fty} K_n(t_1, \dots, t_n)x(t_1) \dots x(t_n) dt_1 \dots dt_n — такова общая форма ряда, где K_n — ядра, описывающие n-ую степень нелинейности. Использование данного подхода позволяет эффективно моделировать искажения, вызванные нелинейными элементами в системе, и получать более реалистичные и точные прогнозы поведения сигнала. Это особенно важно в задачах, где традиционные линейные методы оказываются недостаточно эффективными из-за значительных нелинейных искажений.
Интеграция рядов Вольтерры с алгоритмами NSAF-NKP, воплощенная в подходе Volterra-NKP-NSAF, открывает возможности адаптивной фильтрации в нелинейных средах. В отличие от традиционных линейных фильтров, неспособных эффективно справляться с сигналами, подверженными значительным искажениям, данная комбинация позволяет моделировать и компенсировать нелинейные зависимости. Алгоритмы NSAF-NKP обеспечивают адаптацию параметров фильтра на основе поступающего сигнала, в то время как ряды Вольтерры предоставляют мощный инструмент для представления нелинейных систем в виде бесконечной суммы нелинейных интегралов. Это позволяет Volterra-NKP-NSAF эффективно подавлять нелинейные шумы и восстанавливать исходный сигнал с высокой точностью, что особенно важно в таких областях, как обработка изображений, связь и биомедицинская инженерия.
Комбинация алгоритмов Volterra-NKP-NSAF эффективно преодолевает ограничения, свойственные линейной фильтрации, особенно в условиях существенных искажений сигнала. Традиционные линейные фильтры оказываются неспособными адекватно обрабатывать нелинейные искажения, приводя к значительным потерям информации и снижению качества сигнала. В отличие от них, предложенный подход, используя нелинейное моделирование посредством рядов Вольтерры, позволяет учитывать и компенсировать эти искажения. Это приводит к заметному повышению точности восстановления сигнала и улучшению его характеристик в сложных, нелинейных средах, где стандартные методы оказываются недостаточно эффективными. В результате, достигается превосходная производительность в задачах, требующих высокой устойчивости к искажениям и точной обработки нелинейных сигналов.
Предложенная структура, объединяющая надежные методы оценки с моделированием нелинейных систем, представляет собой универсальный инструмент для широкого спектра приложений в обработке сигналов. В отличие от традиционных линейных подходов, которые часто оказываются неэффективными в условиях значительных искажений, данная методика позволяет адаптироваться к сложным нелинейностям, присущим многим реальным сигналам. Это особенно важно в задачах, требующих высокой точности и надежности, таких как восстановление изображений, обработка звука, телекоммуникации и биомедицинская инженерия. Использование робастных оценок гарантирует стабильность и эффективность алгоритмов даже при наличии шумов и погрешностей в данных, что делает данную структуру востребованной в различных областях науки и техники, где точность и надежность являются критическими факторами.
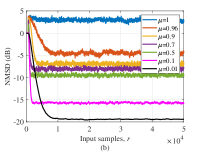
Представленная работа демонстрирует изысканный подход к адаптивной фильтрации, где сложность системы не является препятствием, а скорее вызовом для элегантного решения. Алгоритмы, основанные на ближайшем кронкеровском разложении, позволяют достичь высокой скорости сходимости и снизить вычислительную нагрузку, что особенно ценно в задачах активного шумоподавления и идентификации нелинейных систем. Как говорил Марк Аврелий: «Всё, что происходит с тобой, — это лишь материал для разума». Эта фраза перекликается с принципом, лежащим в основе данной разработки: даже сложные и зашумленные данные могут быть преобразованы в полезный сигнал благодаря тщательному анализу и применению продуманных алгоритмов. Эффективное подавление импульсного шума, достигаемое благодаря предложенному методу, — яркий пример того, как гармония между формой и функцией приводит к превосходному результату.
Куда же дальше?
Представленный подход, использующий разложение на ближайшее кронкеровское произведение в субполосовой адаптивной фильтрации, безусловно, представляет собой шаг вперед. Однако элегантность решения не должна затмевать фундаментальные вопросы. Остается открытым вопрос о том, насколько эффективно данная методика масштабируется при работе с системами, чья нелинейность не поддается адекватной аппроксимации в выбранных субполосах. Или, проще говоря, как сохранить изящество при усложнении задачи.
Очевидным направлением дальнейших исследований представляется адаптация алгоритма к нестационарным средам. Реальный мир редко предлагает стабильные условия. Потребуется разработка методов, позволяющих алгоритму быстро адаптироваться к изменяющимся характеристикам шума и нелинейностей, не теряя при этом скорости сходимости и устойчивости. Возможно, стоит обратить внимание на комбинацию с рекуррентными нейронными сетями, чтобы получить систему, способную к самообучению и прогнозированию.
Наконец, практическая реализация всегда диктует свои условия. Оптимизация для встраиваемых систем с ограниченными ресурсами — это не просто техническая задача, а искусство компромисса. Упрощение алгоритма без потери критически важных характеристик — вот истинный вызов для исследователя. И, конечно, необходимо помнить, что любое решение должно быть не только эффективным, но и понятным — как хорошо спроектированный интерфейс.
Оригинал статьи: https://arxiv.org/pdf/2601.10078.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Статья также опубликована на личном сайте автора.