Квантовые технологии
Эхо чёрных дыр: как квантовая гравитация меняет гравитационные волны
Автор: Денис Аветисян
Новое исследование показывает, как квантовые поправки, основанные на петлевой квантовой гравитации, влияют на затухающие колебания гравитационных волн, возникающих при слиянии чёрных дыр.
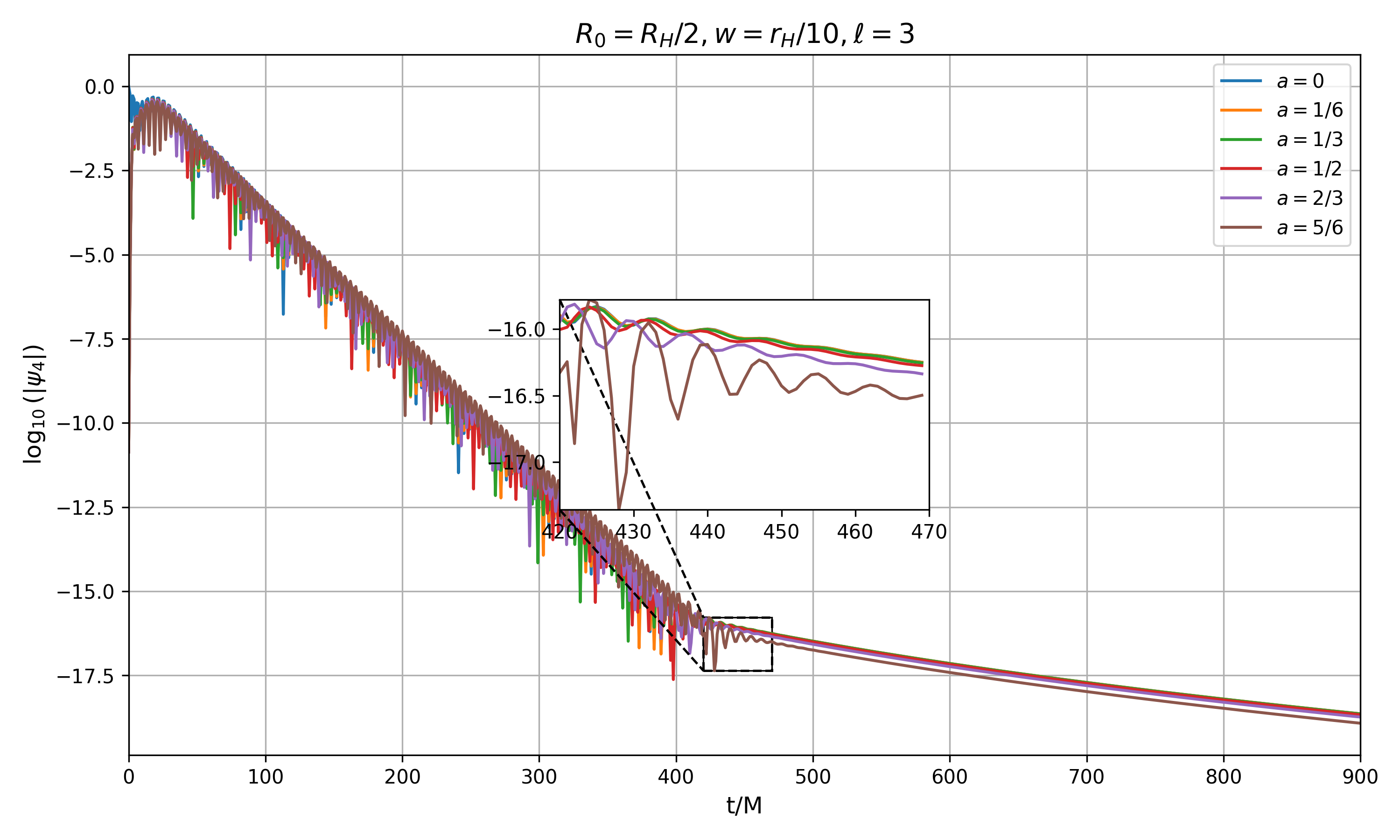
Исследование посвящено анализу влияния квантовых поправок на поздние стадии эволюции гравитационных волн, излучаемых при слиянии чёрных дыр, используя формализм NP и методы петлевой квантовой гравитации.
Несмотря на успехи общей теории относительности, применительно к сильным гравитационным полям, остаются вопросы о природе черных дыр на квантовом уровне. В работе ‘Gravitational Wave Tails and Transient Behaviors of Quantum-Corrected Black Holes’ исследуется влияние квантовых поправок, полученных в рамках эффективной петлевой квантовой гравитации, на затухающие хвосты гравитационных волн, возникающих при слиянии черных дыр. Полученные результаты указывают на то, что квантовые эффекты могут изменять амплитуду и переходные характеристики этих хвостов, что потенциально влияет на наблюдаемую картину гравитационных волн. Возможно ли, что будущие наблюдения позволят выявить эти квантовые поправки и глубже понять структуру черных дыр?
Предел Классической Гравитации: Где Эйнштейн Молчит
Более столетия общая теория относительности Эйнштейна успешно описывала гравитацию, предсказывая и объясняя множество астрономических явлений. Однако, при рассмотрении сингулярностей — точек, где плотность и кривизна пространства-времени становятся бесконечными, например, в центре чёрных дыр — эта теория демонстрирует свою неспособность. Математические уравнения перестают давать физически осмысленные решения, предсказывая бесконечные значения физических величин. Это указывает на то, что общая теория относительности является лишь приближением к более фундаментальной теории гравитации, способной корректно описывать поведение пространства-времени в экстремальных условиях. По сути, она точно работает в большинстве случаев, но терпит крах именно там, где гравитация становится наиболее сильной и проявляются квантовые эффекты, требуя нового подхода к пониманию фундаментальных сил природы.
Ограничения общей теории относительности в экстремальных гравитационных условиях, таких как сингулярности черных дыр, указывают на необходимость разработки квантовой теории гравитации. Классическое описание гравитации, столь успешное в большинстве случаев, оказывается недостаточным при описании областей, где гравитационные силы чрезвычайно сильны и проявляются квантовые эффекты. Поскольку существующие модели черных дыр основаны на классических метриках, возникает потребность в теории, способной объединить принципы общей теории относительности и квантовой механики. Такая теория позволит не только глубже понять природу черных дыр, но и объяснить процессы, происходящие в самых ранних этапах существования Вселенной, где гравитация и квантовые явления были неразрывно связаны. Разработка квантовой теории гравитации является одной из главных задач современной теоретической физики, поскольку она откроет путь к пониманию фундаментальных законов, управляющих Вселенной на самых базовых уровнях.
Современные представления о чёрных дырах в значительной степени опираются на классические метрики, такие как метрика Шварцшильда и Керра, которые успешно описывают гравитационное поле в рамках общей теории относительности. Однако, эти метрики являются решениями уравнений Эйнштейна в классическом пределе и не учитывают квантовые эффекты, которые становятся доминирующими вблизи сингулярности. Предполагается, что на планковских масштабах, где гравитация становится сравнимой по силе с другими фундаментальными взаимодействиями, классическое описание пространства-времени перестает быть адекватным. Игнорирование этих квантовых эффектов может привести к неполному пониманию физики чёрных дыр, включая процессы испарения \hbar , природу информационного парадокса и истинную структуру сингулярности, что потенциально скрывает важные аспекты их поведения и взаимодействия с окружающей Вселенной.
Понимание природы чёрных дыр является ключевым для расшифровки информации, переносимой гравитационными волнами. Эти возмущения пространства-времени, возникающие при слиянии чёрных дыр или других катастрофических космических событиях, несут в себе данные о массах, спинах и расстояниях до источников. Однако, интерпретация этих сигналов требует точного знания того, как гравитация ведёт себя в экстремальных условиях, близких к горизонту событий чёрной дыры. Классическая общая теория относительности, хоть и успешно описывает гравитацию в большинстве случаев, может быть недостаточной для адекватного анализа сигналов, особенно вблизи сингулярностей. Поэтому, углублённое изучение структуры чёрных дыр, включая возможные квантовые эффекты, необходимо для получения полной и достоверной картины Вселенной, «услышанной» через гравитационные волны, и для проверки фундаментальных физических теорий.
Квантовые Коррекции: Новая Геометрия Пространства-Времени
Петлевая квантовая гравитация (ПКГ) представляет собой теоретическую основу для квантования гравитации, направленную на разрешение сингулярностей, возникающих в классической общей теории относительности, в частности, внутри чёрных дыр. В рамках ПКГ, пространство-время не является гладким континуумом на планковских масштабах, а состоит из дискретных квантов объёма и площади. Это приводит к модификации геометрии пространства-времени на экстремальных плотностях, предотвращая формирование сингулярности в центре чёрной дыры и заменяя её областью высокой, но конечной плотности. Ключевым результатом является предсказание о замене классической сингулярности на «белый дыр» или «мост Эйнштейна-Розена», хотя физическая реализуемость этих решений остаётся предметом исследований. Данный подход отличается от других попыток квантования гравитации, таких как теория струн, и предлагает альтернативный способ описания гравитации на квантовом уровне.
Эффективное описание пространства-времени представляет собой методологию моделирования квантовых гравитационных эффектов посредством модификации классической геометрии пространства-времени. В рамках этого подхода, метрика пространства-времени, описывающая гравитационное поле, подвергается поправкам, учитывающим квантовые флуктуации и другие эффекты, предсказываемые теорией квантовой гравитации. Эти поправки обычно вводятся как небольшие отклонения от классической метрики, что позволяет использовать хорошо развитые инструменты общей теории относительности для анализа модифицированных решений. В частности, изменения в метрике g_{\mu\nu} могут быть введены через добавление членов, зависящих от кривизны пространства-времени или других геометрических величин, эффективно изменяя гравитационное взаимодействие на квантовом уровне и позволяя изучать поведение черных дыр и космологических моделей в условиях, где классическая общая теория относительности неприменима.
Метрика Фридмана — Леметра — Робертсона — Уокера (ФЛРВ) служит основой для построения модифицированных пространств-времен в рамках квантовой гравитации. ФЛРВ описывает однородные и изотропные вселенные и является стандартным решением в космологии для моделирования расширяющейся Вселенной. В контексте квантовой гравитации, эта метрика используется как фоновое пространство, на котором вводятся квантовые поправки, изменяющие геометрию пространства-времени на планковских масштабах. Модификации метрики ФЛРВ позволяют исследовать влияние квантовых эффектов на структуру чёрных дыр и гравитационные волны, отклоняясь от предсказаний классической общей теории относительности. Использование ФЛРВ упрощает расчеты, позволяя сосредоточиться на влиянии квантовых поправок на крупномасштабную структуру пространства-времени, в частности, на параметры, определяющие горизонт событий и распространение гравитационного излучения. ds^2 = -dt^2 + a(t)^2 \left( \frac{dr^2}{1-kr^2} + r^2 d\theta^2 + r^2 \sin^2 \theta d\phi^2 \right) — стандартная форма метрики ФЛРВ, где a(t) — масштабный фактор, а k — параметр кривизны.
Подходы квантовой гравитации, такие как петлевая квантовая гравитация и эффективное описание пространства-времени, предсказывают отклонения от классической структуры чёрных дыр. В частности, эти модели допускают возможность устранения горизонта событий, заменяя его некоторой формой квантового барьера или модифицированной геометрии. Кроме того, квантовые поправки влияют на так называемые “хвосты” гравитационных волн — остаточные колебания, возникающие после основного сигнала, и их характеристики — амплитуда и временной профиль — также модифицируются. Наблюдение этих изменений в амплитуде и переходных процессах гравитационных волн, зарегистрированных детекторами, может предоставить экспериментальные доказательства квантовой природы гравитации и проверить предсказания различных теорий квантовой гравитации. Анализ этих сигналов требует точного моделирования волновой формы сигнала, учитывающего как классические, так и квантовые эффекты.
Декодирование Гравитационных Волн: Квантовый Отпечаток
Формализм Тейколски, базирующийся на формализме Ньюмана-Пенроуза, представляет собой математический аппарат для вычисления излучения гравитационных волн. Формализм Ньюмана-Пенроуза определяет ключевые величины, такие как скаляр Вейля \Psi_4, описывающий приливные силы в пространстве-времени, и использует их для упрощения уравнений Эйнштейна в криволинейных координатах. Формализм Тейколски расширяет этот подход, позволяя решать уравнение возмущений для метрики в случае осесимметричного пространства-времени, что существенно для моделирования гравитационных волн, генерируемых вращающимися черными дырами и нейтронными звездами. Полученные решения позволяют аналитически вычислять амплитуду и фазу гравитационных волн, а также их зависимость от параметров источника.
Формализм Ньюмена-Пенроуза определяет ключевые величины, такие как скаляр Вейля \Psi_4, который описывает приливные силы в пространстве-времени. Скаляр Вейля является комплексно-значимой функцией, отражающей гравитационное поле, испытываемое испытывающей частицей. Он непосредственно связан с компонентами тензора кривизны Римана и характеризует величину приливных сил, действующих на малые геодезические отклонения. По сути, скаляр Вейля предоставляет информацию о гравитационных градиентах и искажениях, возникающих вокруг массивных объектов, и играет критическую роль в анализе и интерпретации сигналов гравитационных волн, поскольку он определяет вклад приливных эффектов в наблюдаемую форму волны.
Численные методы, такие как Horizon-Penetrating Compactification (компактификация, проникающая за горизонт событий), применяются для решения уравнений Эйнштейна и моделирования гравитационного излучения в ситуациях, когда аналитические решения невозможны. Этот метод позволяет эффективно описывать геометрию пространства-времени вблизи черных дыр и других компактных объектов, избегая сингулярностей и упрощая вычисления. Он предполагает компактификацию внешних областей пространства-времени, что позволяет использовать более компактные численные сетки и снизить вычислительную сложность при моделировании распространения гравитационных волн, особенно в сильных гравитационных полях. Применение Horizon-Penetrating Compactification требует решения сложных дифференциальных уравнений в частных производных, для чего используются различные численные схемы и алгоритмы, оптимизированные для высокопроизводительных вычислений.
Квантовые поправки вносят изменения в квазинормальные моды (QNM) и «поздние хвосты» (late-time tails) гравитационных волн, что может служить потенциальной наблюдаемой сигнатурой. Изменения QNM проявляются в сдвиге частоты и скорости затухания, влияя на спектральную форму сигнала. «Поздние хвосты» представляют собой спадающие колебания амплитуды, возникающие после основного сигнала, и их характеристики — амплитуда и временной профиль — также модифицируются. Наблюдение этих изменений в амплитуде и переходных процессах гравитационных волн, зарегистрированных детекторами, может предоставить экспериментальные доказательства квантовой природы гравитации и проверить предсказания различных теорий квантовой гравитации. Анализ этих сигналов требует точного моделирования волновой формы сигнала, учитывающего как классические, так и квантовые эффекты.
Экзотические Альтернативы и Наблюдательные Перспективы
Вместо классических чёрных дыр, предсказывающих сингулярность — точку бесконечной плотности и нарушение известных законов физики — современные исследования рассматривают возможность существования экзотических компактных объектов. Эти объекты, обладающие чрезвычайно высокой плотностью, не формируют горизонт событий — границу, за которой ничто, даже свет, не может вырваться. Отсутствие горизонта событий принципиально решает проблему сингулярности, позволяя избежать математических трудностей и потенциальных противоречий с фундаментальными принципами физики. Такие объекты, хотя и похожи на чёрные дыры внешне, могут обладать иными внутренними структурами и свойствами, что открывает новые возможности для проверки теорий квантовой гравитации. Изучение их характеристик, особенно через анализ гравитационных волн, может предоставить ключевые данные для понимания природы гравитации в экстремальных условиях и поиска альтернативных моделей коллапсирующих звёзд.
Коэффициенты вращения Риччи, являющиеся ключевыми элементами формализма Ньюмена-Пенроуза, детально описывают вращение пространства-времени вокруг компактных объектов. Эти коэффициенты не просто отражают угловую скорость, но и определяют, как гравитационные волны, испускаемые этими объектами, будут искажать пространство-время. Вращение пространства-времени, определяемое этими коэффициентами, влияет на поляризацию и амплитуду испускаемых сигналов, что позволяет, теоретически, отличить экзотические компактные объекты от классических чёрных дыр. Анализ этих коэффициентов позволяет моделировать и предсказывать специфические особенности гравитационного излучения, связанные с вращением, что является критически важным для интерпретации данных, получаемых от будущих детекторов гравитационных волн. \Psi_0 , \Psi_1 , \Psi_2 , \Psi_3 , \Psi_4 — примеры псевдотензорных величин, вычисляемых на основе коэффициентов Риччи и несущих информацию о геометрии пространства-времени.
Понимание нулевого тетрада имеет первостепенное значение при интерпретации свойств пространства-времени в рамках данных вычислений. Этот математический инструмент, разработанный в рамках формализма Ньюмена-Пенроуза, позволяет выделить нулевые направления — пути, по которым свет и другие безмассовые частицы распространяются в искривленном пространстве-времени. Корректное построение нулевого тетрада необходимо для выделения аффинных параметров, определяющих геодезические — траектории движения частиц в гравитационном поле. Именно через этот тетрад выражаются ключевые величины, описывающие гравитационное поле, такие как тензор Вейля и скаляр Риччи, что позволяет точно рассчитывать излучение Хокинга и другие эффекты, связанные с квантовой гравитацией. Неточности в определении нулевого тетрада могут привести к искажению результатов и неверной интерпретации физических свойств экзотических компактных объектов, таких как квантовые черные дыры или их альтернативы.
Предстоящее поколение гравитационно-волновых детекторов, таких как Einstein Telescope и Cosmic Explorer, обладает беспрецедентной чувствительностью, способной уловить тончайшие различия в сигналах, испускаемых экзотическими компактными объектами. Эти различия, проявляющиеся в небольших отклонениях от предсказаний общей теории относительности, могут стать ключом к проверке различных моделей квантовой гравитации. Анализ характеристик гравитационных волн, в частности, формы волны и поляризации, позволит исследователям отличить сценарии, где вместо сингулярности в центре черной дыры существует экзотический объект без горизонта событий. Успешное обнаружение этих отличий не только подтвердит или опровергнет конкретные теоретические предсказания, но и откроет новые горизонты в понимании природы гравитации на самых экстремальных масштабах, предоставив эмпирические данные для построения более полной и точной теории, объединяющей квантовую механику и общую теорию относительности.
Исследование поздних стадий гравитационных волн, вызванных слиянием чёрных дыр, демонстрирует, как квантовые поправки, возникающие из петлевой квантовой гравитации, влияют на амплитуду и фазовый переход этих волн. Это напоминает о том, как легко даже самые точные модели подвержены влиянию непредсказуемых факторов. Как заметил Иммануил Кант: “Всё наше знание начинается с чувств, но продолжается благодаря разуму”. В данном случае, чувства — это наблюдаемые гравитационные волны, а разум — попытки построить теоретическую модель. Однако, как показывает работа, даже самые изощренные модели, основанные на разуме, могут быть скорректированы, когда сталкиваются с реальностью квантовых эффектов, проявляющихся в виде ‘хвостов’ гравитационных волн. В конечном итоге, понимание этих квантовых ‘хвостов’ требует пристального внимания к тому, как моделируются сами предположения и ожидания исследователей.
Что дальше?
Исследование поздних стадий гравитационных волн, вызванных слиянием чёрных дыр, и влияние на них квантовых поправок, полученных из петлевой квантовой гравитации, неизбежно наталкивает на вопрос не столько о физике чёрных дыр, сколько о физике наблюдателя. Моделирование этих “хвостов” гравитационных волн — это, по сути, попытка предсказать не поведение Вселенной, а то, как человеческий разум интерпретирует её шум. Текущие ограничения наблюдательных возможностей, упомянутые в работе, — не техническая проблема, а отражение нашей ограниченной способности различать реальность и проекцию собственных ожиданий.
Очевидным направлением дальнейших исследований является расширение формализма NP для включения более сложных квантовых эффектов. Однако, более плодотворным может оказаться переосмысление самого подхода. Вместо того чтобы стремиться к все более точным моделям, возможно, стоит сосредоточиться на понимании того, какие упрощения и идеализации неизбежно вносятся в процесс моделирования, и как эти искажения влияют на интерпретацию результатов. Ведь, в конечном счете, даже самые изысканные математические конструкции — лишь карты, а не сама территория.
Вопрос о наблюдаемости этих квантовых поправок остаётся открытым, и, возможно, принципиально неразрешимым. Важно помнить, что отсутствие доказательств не является доказательством отсутствия. Невозможность обнаружить что-либо в данный момент времени не означает, что это не существует, а лишь свидетельствует о несовершенстве наших инструментов и ограниченности нашего восприятия. И в этом кроется парадокс: чем больше узнаём о Вселенной, тем яснее понимаем, что остаётся непознанным.
Оригинал статьи: https://arxiv.org/pdf/2601.00164.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Статья также опубликована на личном сайте автора.