Квантовый взгляд на атомные ядра: преодолевая шум и сложность

---

Новое исследование демонстрирует прогресс в моделировании атомных ядер на квантовых компьютерах, открывая путь к более точным и эффективным расчетам.

Работа посвящена снижению затрат на измерения и смягчению ошибок в ab initio квантовых вычислениях легких ядер, используя вариационный квантовый алгоритм (VQE) и методы симметрийной проекции.

Несмотря на огромный потенциал квантовых вычислений в моделировании сложных квантовых систем, реализация этого потенциала на существующих зашумленных квантовых устройствах представляет собой серьезную задачу. В работе, озаглавленной ‘Toward $\text{Ab Initio}$ Quantum Simulations of Atomic Nuclei Using Noisy Qubits’, продемонстрированы квантовые симуляции расчетов модели оболочки без центрального ядра для ядра трития с учетом двух- и трех-нуклонных сил. Значительное снижение стоимости измерений достигнуто за счет использования группировки измерений и оптимизации, а также применением проецирования на число частиц для смягчения влияния шума. Открывает ли это путь к более точным и эффективным квантовым вычислениям свойств атомных ядер и, в конечном итоге, к пониманию фундаментальных сил, определяющих структуру материи?

---

Вычислительные Пределы в Изучении Ядерной Структуры

Точное моделирование структуры атомных ядер, имеющее решающее значение для астрофизики и материаловедения, сталкивается с серьезными вычислительными ограничениями. Сложность заключается в том, что для описания даже относительно небольших ядер требуется огромный объем ресурсов. Это связано с тем, что каждый нуклон (протон или нейтрон) взаимодействует со всеми остальными, что приводит к экспоненциальному росту вычислительной нагрузки с увеличением числа нуклонов. Таким образом, моделирование более сложных ядер, необходимых для понимания процессов, происходящих в звездах или в новых материалах, становится практически невозможным при использовании традиционных методов. Несмотря на значительный прогресс в вычислительной технике, существующие алгоритмы часто оказываются недостаточными для достижения необходимой точности и скорости расчетов, что создает серьезную проблему для развития этих важных областей науки.

Традиционные методы моделирования атомных ядер, основанные на решении Schrödinger уравнения, сталкиваются с фундаментальным ограничением: вычислительная сложность растет экспоненциально с увеличением числа нуклонов — протонов и нейтронов, составляющих ядро. Это означает, что даже умеренно сложные ядра, состоящие из нескольких десятков нуклонов, становятся практически недоступными для точного расчета. Каждый добавленный нуклон требует экспоненциально больше вычислительных ресурсов, что делает моделирование крупных ядер непосильной задачей для современных компьютеров. В результате, понимание структуры и свойств тяжелых ядер, имеющих важное значение для астрофизики и материаловедения, остается серьезной проблемой, требующей разработки принципиально новых вычислительных подходов.

Точность моделирования атомных ядер напрямую зависит от учета всех значимых сил взаимодействия между нуклонами. В то время как двухчастичное взаимодействие достаточно хорошо изучено и относительно легко включается в расчеты, трехчастичное взаимодействие представляет собой серьезную проблему. Это связано с тем, что его учет требует экспоненциального увеличения вычислительных ресурсов с ростом числа нуклонов в ядре. Включение трехчастичной силы необходимо для точного предсказания свойств ядер, особенно экзотических изотопов, однако сложность расчета быстро становится непосильной даже для самых мощных суперкомпьютеров. Таким образом, трехчастичное взаимодействие является ключевым фактором, ограничивающим возможности современных методов моделирования ядерной структуры и стимулирующим поиск инновационных вычислительных подходов.

Ограничения существующих вычислительных методов в изучении структуры атомных ядер стимулируют поиск инновационных подходов, способных преодолеть присущие им проблемы масштабируемости. Традиционные алгоритмы, сталкиваясь с экспоненциальным ростом вычислительных затрат при увеличении числа нуклонов, становятся неприменимыми к сложным системам. В связи с этим, активно исследуются альтернативные методы, такие как тензорные сети и методы Монте-Карло, направленные на снижение вычислительной сложности без ущерба для точности моделирования. Эти новые подходы позволяют более эффективно учитывать важные взаимодействия между нуклонами, включая трехчастичные силы, что критически важно для предсказания свойств ядер и понимания процессов, происходящих в астрофизических средах и при создании новых материалов. Разработка и оптимизация этих методов представляют собой ключевую задачу современной ядерной физики, открывающую перспективы для углубленного изучения структуры материи во Вселенной.

Квантовые Вычисления: Новый Горизонт в Ядерной Физике

Квантовые вычисления предоставляют перспективный подход к преодолению ограничений, присущих классическим методам в ядерной физике. Традиционные вычислительные подходы сталкиваются со сложностями при моделировании многочастичных систем, таких как атомные ядра, из-за экспоненциального роста вычислительных затрат с увеличением числа нуклонов. Это связано с тем, что классические компьютеры неэффективно обрабатывают квантовую запутанность и суперпозицию, являющиеся фундаментальными свойствами ядерной материи. Квантовые компьютеры, напротив, используют эти квантовые явления для выполнения вычислений, потенциально позволяя моделировать более сложные ядерные системы и решать задачи, недоступные для классических алгоритмов. Это открывает возможности для более точного предсказания свойств ядер, понимания ядерных реакций и разработки новых технологий в области энергетики и медицины.

Использование принципов квантовой механики позволяет непосредственно моделировать квантовое поведение нуклонов, в отличие от классических методов, которые часто прибегают к приближениям. В ядре атома нуклоны, такие как протоны и нейтроны, взаимодействуют посредством сильного взаимодействия, описываемого квантовой хромодинамикой. Непосредственное решение Schrödinger equation для многочастичной системы нуклонов является вычислительно сложной задачей для классических компьютеров. Квантовые симуляции, напротив, используют кубиты для представления квантовых состояний нуклонов и их взаимодействий, что позволяет более эффективно описывать сложные корреляции и эффекты, возникающие в ядре. Это позволяет исследовать структуры и реакции ядер с большей точностью и предсказывать их свойства, невозможные для классического моделирования.

Применение квантовых алгоритмов в рамках расчетов Ab Initio позволяет более эффективно представлять многочастичную волновую функцию ядра по сравнению с классическими подходами. Классические методы испытывают экспоненциальные трудности при моделировании систем из-за необходимости хранения и обработки информации о корреляциях между всеми нуклонами. Квантовые алгоритмы, такие как вариационный квантовый собственный решатель (VQE) и квантовый фазовый оценщик (QPE), используют квантовую суперпозицию и запутанность для кодирования волновой функции в кубитах, что потенциально снижает вычислительную сложность и позволяет моделировать ядра с большей точностью и для большего числа нуклонов. Эффективность представления зависит от выбора конкретного алгоритма и используемого квантового оборудования.

Несмотря на потенциал квантовых вычислений для моделирования ядерных систем, точность этих симуляций ограничена стоимостью и сложностью точного измерения соответствующих квантовых свойств. Определение параметров взаимодействия между нуклонами, а также корреляций в многочастичной волновой функции, требует значительных вычислительных ресурсов даже для квантовых алгоритмов. Кроме того, точность измерения таких свойств, как радиусы зарядового распределения, моменты и другие наблюдаемые величины, напрямую влияет на достоверность результатов моделирования. Погрешности в определении этих параметров приводят к систематическим ошибкам в предсказаниях, что ограничивает применимость квантовых симуляций для решения конкретных задач ядерной физики. Таким образом, даже с использованием квантовых компьютеров, необходимость в высокоточных экспериментальных данных остается критически важной.

Минимизация Вычислительных Затрат: Эффективность Квантовых Измерений

Стоимость квантового моделирования напрямую зависит от количества необходимых измерений для получения значимой информации. Каждое измерение в квантовой системе вносит вклад в общую вычислительную сложность, и увеличение числа измерений экспоненциально увеличивает требуемые ресурсы. Поэтому, снижение количества измерений является ключевой задачей для реализации практических квантовых симуляций сложных систем. Эффективность алгоритма моделирования, таким образом, в значительной степени определяется способностью минимизировать количество необходимых измерений при сохранении необходимой точности и достоверности результатов. Для многих задач, особенно связанных с моделированием молекулярных систем, количество необходимых измерений может быть чрезвычайно велико, что делает классические вычислительные методы непрактичными, но также и затрудняет реализацию на существующих квантовых компьютерах.

Представление ядерного гамильтониана в виде Pauli Strings требует измерения большого количества наблюдаемых величин. Каждая строка Паули соответствует определенному оператору, и для полного описания состояния системы необходимо определить вклад каждого оператора. Число необходимых измерений растет экспоненциально с увеличением числа кубитов и сложности гамильтониана, что создает значительные вычислительные трудности при моделировании даже небольших ядерных систем. Для точного определения энергии основного состояния необходимо измерить вклад каждой строки Паули в гамильтониан, что делает задачу крайне ресурсоемкой и ограничивает масштабируемость квантовых симуляций.

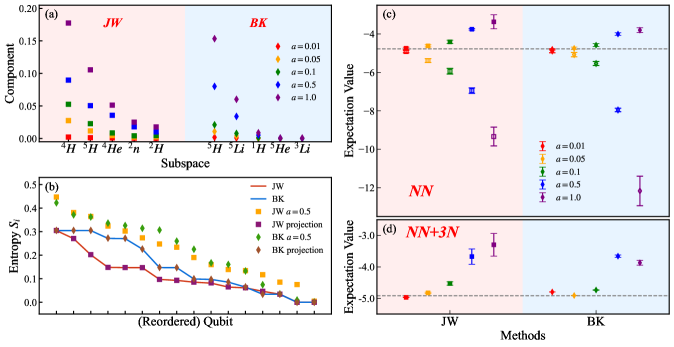
Методы одновременных групповых измерений и симметричной проекции значительно снижают количество необходимых измерений для квантового моделирования, повышая вычислительную эффективность. В частности, при моделировании системы ³H с тремя нуклон-нуклонными взаимодействиями (3NN), применение схемы общей коммутативности (GC) в сочетании с оптимизацией, управляемой теорией возмущений второго порядка (MBPT2), позволило снизить стоимость измерений на 3 порядка величины. Это достигается за счет эффективной группировки операторов и использования симметрий системы, что существенно уменьшает размер пространства состояний, требуемого для точного расчета.

Для минимизации влияния шума на результаты измерений и повышения точности квантовых симуляций применяются методы снижения ошибок (Error Mitigation). В ходе исследований было показано, что перекрытие между волновой функцией, полученной с использованием теории возмущений второго порядка (MBPT2) в качестве направляющего сигнала, и точным волновым решением достигает значения 0.978. Это указывает на высокую степень соответствия между приближенным и точным решениями, что подтверждает эффективность применения методов снижения ошибок для повышения надежности результатов квантовых вычислений.

Схема общей коммутативности (GC) позволила существенно сократить количество группировок при построении гамильтониана, более чем в 10 раз по сравнению с наивным подходом без группировки. Применение схемы GC в сочетании с членами, полученными на основе теории возмущений второго порядка (MBPT2), позволило добиться дальнейшего сокращения количества группировок — более чем в 1000 раз при значении параметра em\_axe\_max=3. Данное снижение числа группировок напрямую ведет к уменьшению числа необходимых измерений при квантовом моделировании, что повышает вычислительную эффективность и масштабируемость.

Валидация и Перспективы: Влияние на Астрофизику и Материаловедение

Эффективность методов снижения количества измерений подтверждается на квантовом устройстве «Kyoto». Исследования, проведенные с использованием этой платформы, демонстрируют значительное улучшение точности расчетов, что позволяет более эффективно моделировать сложные ядерные системы. В частности, применение методов проекции симметрии позволило снизить отклонение диагональных энергий с -8.33 МэВ до 0.04 МэВ, что свидетельствует о существенном прогрессе в области квантовых вычислений и открывает новые возможности для изучения структуры ядра и астрофизических процессов. Успешная реализация этих методов на реальном квантовом оборудовании является важным шагом к созданию более точных и эффективных симуляций, способных решать задачи, недоступные для классических вычислений.

Проверка эффективности предложенных методов снижения вычислительной сложности на реальном квантовом оборудовании, в частности на устройстве `Kyoto Quantum Device`, предоставляет ценные сведения об их масштабируемости и практических ограничениях. Такой подход позволяет выявить узкие места и оценить, насколько хорошо алгоритмы переносят увеличение размеров решаемых задач. Результаты демонстрируют, что, несмотря на значительный прогресс в разработке алгоритмов, их применение к крупномасштабным системам сталкивается с трудностями, связанными с когерентностью кубитов и шумами. Анализ этих ограничений необходим для дальнейшей оптимизации алгоритмов и разработки новых стратегий смягчения ошибок, что, в свою очередь, открывает возможности для более точного моделирования ядерной структуры и расширения границ применимости квантовых вычислений в астрофизике и материаловедении.

Достижения в области снижения вычислительной сложности позволяют проводить более точное и эффективное моделирование структуры атомных ядер, открывая перспективы для прорывов в астрофизике и материаловедении. В частности, применение методов симметрийной проекции значительно повысило точность вычисления диагональных энергий, снизив отклонение от нуля до 0.04 МэВ — существенное улучшение по сравнению с -8.33 МэВ, получаемым без использования подобных методов. Это свидетельствует о возможности получения более реалистичных моделей, необходимых для понимания процессов, происходящих в звёздах, и разработки новых материалов с заданными свойствами. E = mc^2

Дальнейшие исследования направлены на разработку усовершенствованных стратегий смягчения ошибок, что позволит повысить надежность вычислений и расширить возможности моделирования. Особое внимание уделяется применению этих методов к более крупным и сложным ядерным системам, что потребует оптимизации алгоритмов и использования передовых вычислительных ресурсов. Успешная реализация этих задач откроет перспективы для более точного изучения свойств материи в экстремальных условиях, а также для создания новых материалов с заданными характеристиками. В частности, планируется исследовать влияние различных типов ошибок на результаты вычислений и разработать методы их компенсации, что позволит существенно повысить достоверность получаемых результатов и углубить понимание фундаментальных законов природы.

Исследование демонстрирует стремление к математической чистоте в моделировании атомных ядер. Авторы, подобно тем, кто ищет элегантность в алгоритмах, успешно снизили вычислительные издержки, связанные с измерением, за счет группировки данных. Этот подход, наряду с применением методов смягчения ошибок посредством симметрийной проекции, позволяет достичь большей точности в расчетах. Как заметила Мэри Уолстонкрафт: «Недостаточно обладать умом, о нем нужно еще и знать». В данном случае, осознанное применение математических принципов и тщательный контроль над ошибками позволяют раскрыть потенциал квантовых вычислений для решения сложных задач ядерной физики, что особенно важно при использовании вариационного квантового решателя (VQE).

Что Дальше?

Представленные результаты, безусловно, демонстрируют продвижение в направлении расчётов атомных ядер «с нуля» на квантовых компьютерах. Однако, если кажущаяся магия снижения затрат на измерения объясняется лишь группировкой, следует задуматься о фундаментальном пересмотре подхода. Истинная элегантность, как известно, кроется в математической чистоте, а не в хитроумных трюках оптимизации. Очевидно, что вопрос о масштабируемости предложенных методов для более тяжёлых ядер остаётся открытым. Ведь, как гласит старая истина, решение, работающее на нескольких кубитах, не обязательно будет работать на сотнях.

Особенно остро стоит вопрос об ошибках. Симметричная проекция, несомненно, смягчает некоторые из них, но полагаться исключительно на методы пост-обработки — наивность. Необходимо разрабатывать квантовые алгоритмы, изначально устойчивые к шуму. Иначе, все усилия по снижению стоимости измерений будут бессмысленны, если результат будет погрешённым из-за неконтролируемых ошибок. Трехчастичные силы, как и всегда, остаются серьёзным препятствием, требующим дальнейшего изучения и разработки более эффективных методов их учёта.

В конечном итоге, успех в этой области требует не просто увеличения количества кубитов, а создания квантовых компьютеров, способных выполнять сложные вычисления с высокой точностью. Если же этого не произойдёт, то все «ab initio» расчёты останутся лишь красивой математической абстракцией, далёкой от реальности физических ядер.

---

Оригинал статьи: https://arxiv.org/pdf/2601.00315.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/