Квантовые технологии
Шахматный вызов для квантовых алгоритмов
Автор: Денис Аветисян
Новая задача, основанная на шахматных тактиках, позволяет оценить эффективность квантовой оптимизации и продемонстрировать преимущества «умных» стратегий.

Исследование показывает, что использование ограничений и предварительной инициализации значительно улучшает производительность QAOA на структурированных задачах, таких как задача доминирования кольца короля в шахматах.
Несмотря на успехи квантового алгоритма QAOA на синтетических задачах, его эффективность на реальных проблемах с осмысленными ограничениями остаётся малоизученной. В работе «Quantum King-Ring Domination in Chess: A QAOA Approach» представлен новый эталон QKRD, основанный на шахматных позициях, предоставляющий 5000 структурированных экземпляров для оценки алгоритмов. Показано, что учет специфики задачи, например, использование сохраняющих ограничения миксеров и стратегий «тёплого старта», значительно ускоряет сходимость QAOA по сравнению со случайными эталонами. Сможет ли структурированный подход к разработке эталонов выявить скрытые преимущества проблемно-ориентированных квантовых алгоритмов и приблизить нас к практическому квантовому превосходству?
Преодолевая Ограничения Стандартных Эталонов: Необходимость Семантической Структуры
Традиционные эталоны для квантового приближенного оптимизационного алгоритма (QAOA), такие как задача MaxCut на случайных графах и варианты задачи коммивояжера, зачастую оказываются слишком абстрактными и лишены семантической насыщенности, присущей реальным задачам. Эти упрощенные модели не способны отразить сложные ограничения и закономерности, которые часто встречаются в практических приложениях, будь то оптимизация логистических маршрутов, разработка новых материалов или финансовое моделирование. В результате, оценка производительности QAOA на подобных эталонах предоставляет ограниченное понимание его потенциала для решения действительно сложных и значимых задач, возникающих в реальном мире. Отсутствие семантической близости к реальным проблемам затрудняет экстраполяцию результатов, полученных на абстрактных эталонах, и сдерживает прогресс в разработке квантовых алгоритмов, способных принести ощутимую пользу.
Абстрактные формулировки, используемые в стандартных тестах для квантового приближенного алгоритма оптимизации (QAOA), зачастую не отражают сложность реальных задач, имеющих внутреннюю структуру. В отличие от искусственно созданных проблем, многие практические задачи характеризуются сложными взаимосвязями, ограничениями и паттернами, которые не учитываются в упрощенных моделях. Например, задачи логистики, планирования или машинного обучения обладают специфическими свойствами, определяемыми предметной областью. Игнорирование этих особенностей приводит к тому, что результаты, полученные на абстрактных тестах, не позволяют достоверно оценить потенциал QAOA для решения действительно сложных и значимых проблем, что затрудняет прогресс в области квантовых вычислений и их применений.
Оценка квантового приближенного оптимального алгоритма (QAOA) на стандартных эталонных задачах, таких как случайный граф MaxCut и варианты задачи коммивояжера, дает весьма ограниченное представление о его реальных возможностях при решении сложных, практически значимых проблем. Эти абстрактные формулировки, лишенные семантической насыщенности, не отражают присущие реальным задачам ограничения и закономерности. В результате, достижения на этих упрощенных тестах не гарантируют успешного применения QAOA к задачам, имеющим сложную структуру и требующим учета множества взаимосвязанных факторов. Поэтому, для адекватной оценки потенциала QAOA необходимо использовать эталонные задачи, которые более точно имитируют сложность и специфику реальных вычислительных проблем, позволяя выявить сильные и слабые стороны алгоритма в условиях, приближенных к практическим приложениям.
QKRD: Шахматный Ландшафт для Оптимизации
QKRD использует присущую шахматным тактическим позициям структуру, предлагая более осмысленную платформу для тестирования алгоритма QAOA (Quantum Approximate Optimization Algorithm). В отличие от случайных или искусственно созданных ландшафтов оптимизации, QKRD опирается на реальные зависимости между фигурами и их потенциальными ходами. Это позволяет QAOA взаимодействовать с задачами, которые имеют более выраженную структуру и отражают сложные стратегические соображения, свойственные шахматам. Такой подход позволяет более точно оценить способность алгоритма QAOA эффективно использовать структуру задачи для достижения оптимальных решений, что является ключевым аспектом при разработке и улучшении квантовых алгоритмов оптимизации.
В рамках QKRD, для снижения вычислительной сложности и акцентирования стратегического анализа, рассматриваются локализованные области шахматных позиций, определяемые как “Область интереса” (Region of Interest). Вместо анализа всей шахматной доски, алгоритм QAOA применяется исключительно к выбранной области, содержащей, как правило, несколько ключевых фигур и потенциальные тактические возможности. Такой подход позволяет значительно уменьшить размер решаемой задачи, концентрируясь на стратегически важных аспектах позиции и требуя от QAOA более эффективного использования структуры проблемы в ограниченном пространстве. Ограничение области анализа не только ускоряет процесс оптимизации, но и позволяет более детально изучить способность QAOA к решению задач, требующих сложного стратегического планирования в условиях ограниченных ресурсов.
В QKRD наличие тактических мотивов, таких как двойной удар, вилка или связка, создает специфические ограничения для алгоритма QAOA. Эти мотивы, являясь локальными паттернами в шахматной позиции, требуют от QAOA не просто нахождения глобального минимума энергии, но и учета взаимосвязей между фигурами, участвующими в этих тактических комбинациях. Это усложняет процесс оптимизации, поскольку стандартные методы QAOA, ориентированные на более общие структуры, могут испытывать трудности в эффективном использовании информации, заложенной в этих локальных ограничениях. Наличие тактических мотивов, таким образом, служит своеобразным «стресс-тестом» для QAOA, проверяя его способность адаптироваться к задачам с ярко выраженными локальными зависимостями и ограничениями.
Сохранение Ограничений: Путь к Эффективному Исследованию
Стандартный X миксер, несмотря на свою универсальность, требует добавления штрафных членов (Penalty Terms) для обеспечения соблюдения ограничений, накладываемых на решаемую задачу. Введение таких штрафных членов усложняет процесс оптимизации и может приводить к получению субоптимальных решений, поскольку штрафные функции часто не идеально соответствуют исходным ограничениям, искажая ландшафт оптимизации и затрудняя поиск истинного минимума. Необходимость тонкой настройки весов штрафных членов также добавляет дополнительную сложность и требует значительных вычислительных ресурсов.
В отличие от стандартного `X Mixer`, требующего добавления штрафных членов для обеспечения выполнения ограничений, смесители, сохраняющие ограничения, такие как `XY Mixer` и `Domain-Wall Mixer`, обеспечивают допустимость решений на протяжении всего процесса исследования пространства состояний. Это достигается за счет конструкции самих смесителей, которые по определению не выходят за пределы допустимой области, что устраняет необходимость в дополнительных механизмах коррекции и снижает вычислительную сложность алгоритма. Принцип работы этих смесителей основан на использовании операторов, коммутирующих с ограничениями задачи, что позволяет поддерживать допустимость решений без явного наложения штрафов.
Результаты экспериментов показали, что использование constraint-preserving mixers, таких как XY Mixer и Domain-Wall Mixer, обеспечивает сходимость алгоритма примерно на 13 шагов быстрее, чем стандартный X Mixer (p<10-7). При этом достигается статистически эквивалентный охват (coverage) на бенчмарке QKRD. Данное наблюдение подчеркивает преимущества применения методов, учитывающих специфику решаемой задачи (problem-informed techniques), для алгоритмов, предназначенных для реализации на NISQ-устройствах.

Ускорение Сходимости: Теплые Старты и Оптимизация с Учетом Рисков
Стратегии “горячего старта”, такие как “Базисный горячий старт” и “Локальная суперпозиция горячего старта”, используют принципы классических жадных эвристических алгоритмов для формирования сильных начальных решений в квантовом приближении QAOA. Применяя предварительно вычисленные решения, полученные с помощью жадных алгоритмов, QAOA значительно ускоряет сходимость к оптимальному результату. Этот подход позволяет избежать случайного поиска и сразу же исследовать наиболее перспективные области пространства решений, что особенно важно при решении сложных задач оптимизации. Использование жадных алгоритмов в качестве основы для инициализации QAOA не только повышает эффективность, но и обеспечивает более стабильные и предсказуемые результаты.
Вариант CVaR-QAOA внедряет оптимизацию, учитывающую риски, посредством Shot-Based Estimation, что значительно повышает устойчивость получаемых решений. В отличие от традиционных подходов, которые стремятся к нахождению оптимального решения без учета возможных отклонений, данная методика оценивает не только ожидаемое значение функции потерь, но и ее дисперсию. Оценка производится посредством многократного моделирования (shots), позволяющего получить статистически значимую картину вероятностного распределения решений. Это позволяет алгоритму находить решения, которые не только имеют высокую ожидаемую ценность, но и характеризуются низкой чувствительностью к случайным колебаниям, что особенно важно в задачах, где надежность и предсказуемость результатов имеют первостепенное значение. Таким образом, CVaR-QAOA обеспечивает более стабильные и предсказуемые результаты, особенно в условиях неопределенности и шума.
Исследования показали значительное ускорение сходимости алгоритма QAOA при использовании стратегий “теплых стартов”. В частности, зафиксировано сокращение количества необходимых шагов на 45 (p < 10-100, d=3.35), что свидетельствует о высокой статистической значимости полученных результатов. Более того, QAOA продемонстрировал улучшение покрытия на 12.6% по сравнению с жадным эвристическим алгоритмом и на 80.1% по сравнению со случайным выбором. Эти данные подчеркивают потенциал QAOA для решения структурированных задач оптимизации, при этом величина эффекта превышает 8 стандартных отклонений, что указывает на существенную практическую значимость и надежность алгоритма.
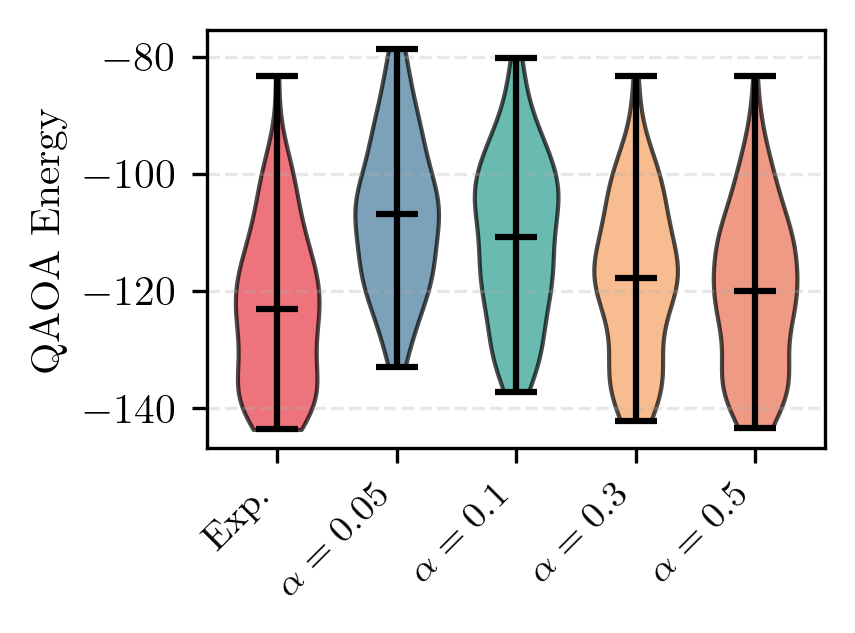
Исследование демонстрирует, что эффективность квантовых алгоритмов, таких как QAOA, тесно связана со структурой решаемой задачи. Авторы подчеркивают важность использования проблемно-ориентированных методов, вроде сохранения ограничений и стратегий «тёплого старта», для достижения значительных улучшений в производительности. Этот подход перекликается с мыслями Ады Лавлейс: «Я считаю, что машиной можно управлять, чтобы она сделала всё, что мы можем сделать, но не более». Подобно тому, как необходимо понимать ограничения машины, представленное исследование указывает на необходимость глубокого понимания структуры задачи для эффективного применения квантовых алгоритмов и раскрытия их потенциала, особенно при решении задач, вдохновленных шахматной тактикой, таких как Quantum King-Ring Domination.
Куда же дальше?
Представленная работа, выявляя преимущества информированных стратегий в квантовой оптимизации на примере задачи доминирования короля в шахматах, лишь подчеркивает фундаментальную истину: элегантность решения рождается не из случайности, а из понимания структуры проблемы. Успех методов, сохраняющих ограничения и использующих «теплый старт», не является неожиданным — это закономерный результат, предсказуемый для системы, где каждая часть взаимосвязана с целым. Однако, вопрос не в том, что эти методы работают, а в том, насколько глубоко мы понимаем почему они работают.
Очевидным следующим шагом представляется расширение спектра задач, используемых в качестве бенчмарков. Случайные задачи, хоть и полезны для базовой оценки, не отражают сложность реальных систем. Необходимо сместить фокус на задачи, имеющие четкую структуру и внутреннюю логику, аналогичную шахматным тактикам. В противном случае, мы рискуем оптимизировать алгоритмы для искусственных сценариев, не имеющих отношения к миру, который стремимся понять и изменить.
И, пожалуй, самое главное: необходимо помнить, что QAOA — лишь один из инструментов. В погоне за квантовым превосходством легко упустить из виду, что фундаментальные принципы оптимизации остаются неизменными. Истинный прогресс заключается не в создании все более сложных алгоритмов, а в углублении нашего понимания систем, которые мы пытаемся оптимизировать, и в использовании этого понимания для создания решений, которые являются не только эффективными, но и элегантными.
Оригинал статьи: https://arxiv.org/pdf/2601.00318.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Статья также опубликована на личном сайте автора.