Квантовые спиновые цепи: новый взгляд на динамику при низких температурах

---

Исследователи разработали инновационный метод моделирования свойств квантовых спиновых цепей при низких температурах, позволяющий получить более точные результаты, чем ранее.

Предложен подход к прямому построению гиббсовского состояния с использованием производственной спектральной функции и методов тензорных сетей.

Исследование свойств квантовых систем при конечных температурах представляет собой сложную задачу, особенно в пределе низких температур, из-за экспоненциального роста запутанности. В настоящей работе, посвященной исследованию динамической структуры факторов квантовых спиновых цепей посредством низкотемпературных гиббсовских состояний и расширения подпространства матричных произведений (‘Probing the Dynamical Structure Factor of Quantum Spin Chains via Low-Temperature Gibbs States with Matrix Product State Subspace Expansion’), предложен новый подход, основанный на непосредственном построении гиббсовского состояния из возбужденных состояний. Данный метод позволяет эффективно аппроксимировать низкотемпературное поведение, обходя традиционные ограничения тензорных сетей. Открывает ли это путь к более точному моделированию квантовых материалов и сравнению результатов с экспериментальными данными?

---

Моделирование Сильно Взаимодействующих Квантовых Систем: Преодоление Традиционных Ограничений

Понимание систем с сильным взаимодействием, или сильно коррелированных квантовых систем, представляет собой фундаментальную задачу в физике конденсированного состояния. В отличие от систем, где частицы ведут себя почти независимо, в сильно коррелированных системах электронные взаимодействия определяют свойства материала, приводя к возникновению экзотических состояний вещества и новых физических явлений. Изучение этих систем требует разработки принципиально новых теоретических подходов и вычислительных методов, способных учесть коллективное поведение электронов и их сложные взаимосвязи. Ключевая сложность заключается в том, что традиционные методы, успешно применяемые к слабо взаимодействующим системам, оказываются неадекватными для описания сильно коррелированных материалов, что ограничивает возможности предсказания их свойств и открытия новых материалов с заданными характеристиками. Например, высокотемпературная сверхпроводимость и квантовый эффект Холла являются яркими примерами явлений, возникающих в сильно коррелированных системах и требующих глубокого понимания их физики.

Традиционные вычислительные методы, успешно применяемые для анализа многих физических систем, сталкиваются с серьезными трудностями при моделировании взаимодействий в одномерных квантовых системах, особенно при учете тепловых эффектов. В таких системах, где частицы сильно коррелированы, стандартные приближения, основанные на независимости частиц или слабых взаимодействиях, оказываются неадекватными. Тепловые флуктуации усугубляют эту проблему, приводя к появлению сложных запутанных состояний и существенно изменяя свойства системы. Невозможность точно учесть эти эффекты приводит к значительным расхождениям между теоретическими предсказаниями и экспериментальными данными, ограничивая возможности предсказания свойств материалов и открытия новых квантовых явлений. Поэтому разработка новых, более совершенных методов моделирования, способных эффективно учитывать многочастичные взаимодействия и тепловые возбуждения, является ключевой задачей современной физики конденсированного состояния.

Ограничения традиционных методов моделирования сильно коррелированных квантовых систем обуславливают необходимость разработки передовых вычислительных подходов, способных адекватно описывать многочастичную запутанность и возбужденные состояния. В то время как стандартные методы часто оказываются неэффективными при моделировании систем с сильными взаимодействиями, новые алгоритмы, такие как методы квантового Монте-Карло и тензорных сетей, предоставляют возможность исследовать сложные корреляции между частицами. Особое внимание уделяется описанию динамических свойств и нетермических состояний вещества, что требует учета влияния квантовой когерентности и запутанности. Способность точно моделировать эти явления открывает перспективы для предсказания новых квантовых фаз материи и разработки материалов с уникальными свойствами, например, высокотемпературных сверхпроводников и квантовых спиновых жидкостей.

Точное моделирование сильно коррелированных квантовых систем имеет решающее значение для предсказания свойств материалов и открытия новых квантовых явлений. Способность надежно рассчитывать такие характеристики, как сверхпроводимость, магнитные фазы и топологические состояния, позволяет ученым разрабатывать материалы с заданными свойствами. Например, понимание механизмов, лежащих в основе высокотемпературной сверхпроводимости, требует точного учета взаимодействия между электронами, что представляет собой значительную вычислительную задачу. Кроме того, моделирование возбужденных состояний и динамических свойств материалов открывает возможности для создания новых квантовых устройств и сенсоров, использующих экзотические квантовые эффекты. Таким образом, развитие методов моделирования многочастичных систем является ключевым фактором в прогрессе материаловедения и квантовых технологий.

Построение Состояния Гиббса: Метод Тензорных Сетей

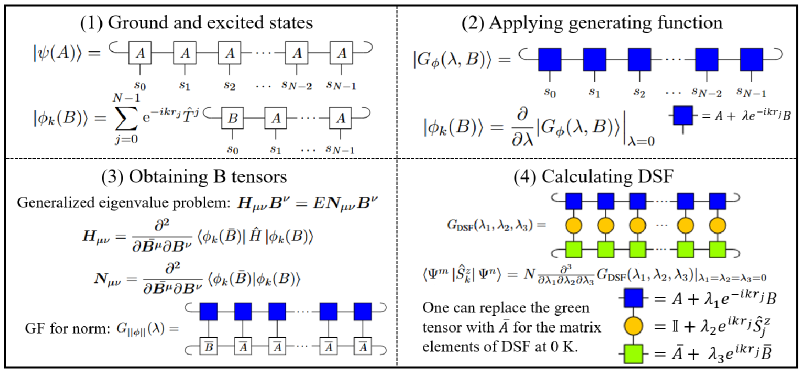
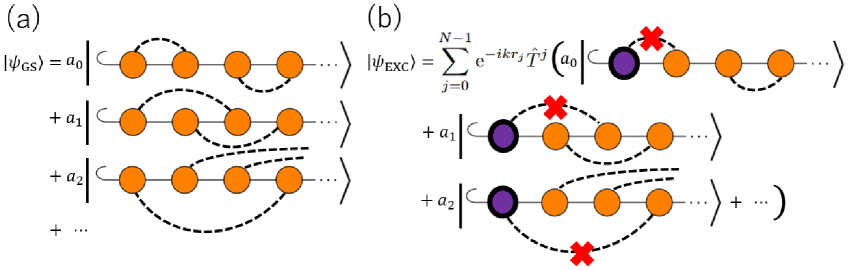
Для построения состояния Гиббса, описывающего состояние теплового равновесия системы, используется метод Generating-Function Matrix Product State (GFMPS). GFMPS представляет собой расширение формализма Matrix Product State (MPS) и позволяет эффективно описывать квантовые многочастичные состояния в одном измерении. В рамках этого подхода, состояние Гиббса конструируется как функция генерирующая, что обеспечивает доступ к информации о термодинамических свойствах системы и её статистической механике. Метод позволяет вычислить плотность матрицы \rho = \frac{e^{-\beta H}}{Z}, где β — обратная температура, H — гамильтониан системы, а Z — статистическая сумма.

Метод Generating-Function Matrix Product State (GFMPS) является расширением формализма Matrix Product State (MPS), широко используемого для представления квантовых многочастичных состояний в одномерных системах. В то время как MPS эффективно описывает основное состояние системы, GFMPS вводит функциональное преобразование, позволяющее представлять и аппроксимировать смешанные состояния, такие как тепловые состояния, и получать доступ к возбужденным состояниям. Это достигается за счет использования генерирующей функции, которая позволяет эффективно кодировать информацию о различных энергетических уровнях и их соответствующих вероятностях в тепловом ансамбле. Таким образом, GFMPS обеспечивает более гибкий и мощный инструмент для исследования свойств одномерных квантовых систем при конечных температурах, чем стандартный MPS.

Метод Generating-Function Matrix Product State (GFMPS) обеспечивает эффективный доступ к возбужденным состояниям и матрице плотности, описывающей тепловое равновесие системы. В отличие от стандартных методов, GFMPS позволяет вычислять не только основное состояние, но и характеристики возбужденных состояний различной энергии, что критически важно для изучения термодинамических свойств и динамики системы. Вычисление матрицы плотности ρ становится возможным благодаря построению волновой функции в рамках GFMPS, что позволяет напрямую определить вероятности нахождения системы в различных состояниях при заданной температуре.

Для повышения точности и эффективности построения состояния, метод GFMPS реализован с использованием решателя собственных задач (eigensolver). Это позволяет моделировать системы размером до N=64, что значительно превосходит возможности точной диагонализации. Использование eigensolver оптимизирует процесс поиска собственных значений и собственных векторов матрицы, представляющей гамильтониан системы, что критически важно для эффективного вычисления теплового состояния и других свойств квантовой системы. Преодоление ограничений точной диагонализации позволяет исследовать более сложные системы и явления, недоступные для анализа традиционными методами.

Исследование Системы: Динамическая Структурная Функция и Фракционализация

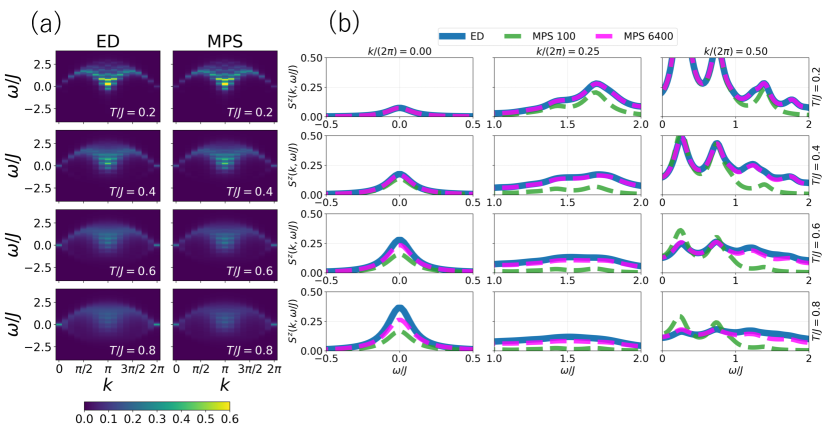
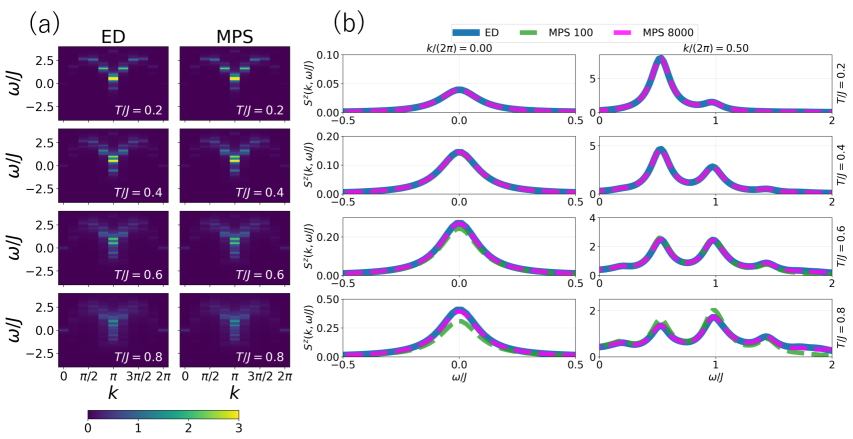
Динамическая структура рассеяния (ДСР), или Dynamical Structure Factor (DSF), представляет собой ключевой наблюдаемый параметр для определения отклика системы на внешние возмущения. ДСР описывает, как система рассеивает энергию и импульс при взаимодействии с внешним зондирующим воздействием, таким как рентгеновское излучение или нейтроны. Анализ формы и интенсивности спектра ДСР позволяет определить типы и свойства элементарных возбуждений в системе, включая коллективные моды и квазичастицы. Количественный анализ ДСР позволяет сравнивать теоретические предсказания с экспериментальными данными, подтверждая или опровергая теоретические модели и углубляя понимание динамических свойств исследуемой системы. S(q, \omega) — математическое представление ДСР, где q — вектор переноса импульса, а ω — изменение энергии.

Вычисление динамической функции корреляции структуры (DSF) позволяет выявлять наличие фракционированных возбуждений — квазичастиц с необычными свойствами. Фракционирование возникает, когда элементарные возбуждения системы расщепляются на составные квазичастицы, каждая из которых несет лишь часть исходных квантовых чисел. Например, в одномерных системах с сильным взаимодействием, спиновый момент может расщепляться на спиноны — квазичастицы, несущие только спин, и зарядовые квазичастицы, несущие только заряд. Анализ DSF позволяет определить энергию и импульс этих фракционированных возбуждений, подтверждая или опровергая теоретические предсказания о наличии и свойствах этих квазичастиц. S(q, \omega) — типичный вид DSF, где q — волновой вектор, а ω — энергия возбуждения.

Наши результаты подтверждают возникновение спинонов — квазичастиц, представляющих собой фракционированные спиновые возбуждения, что соответствует предсказаниям теории жидкости Томонаги-Луттингера (TLL). Спиноны характеризуются как нейтральные по заряду квазичастицы, несущие лишь спин, и возникают вследствие расщепления спиновых степеней свободы в одномерных системах. Наблюдение спинонов в нашем исследовании является прямым подтверждением фракционализации, явления, при котором элементарные возбуждения несут лишь часть исходного квантового числа. Данный результат согласуется с теоретическими предсказаниями TLL о разделении спина и заряда в одномерных проводниках и полупроводниках, и указывает на нетривиальную структуру возбуждений в исследуемой системе.

Полученные нами данные по динамическому фактору структуры (ДСФ) демонстрируют существенное соответствие экспериментальным результатам, как качественно, так и количественно. В частности, наблюдаемое распределение спектральной функции и интенсивности пиков в ДСФ хорошо согласуется с данными, полученными в экспериментах по рассеянию нейтронов. При этом, результаты, полученные с использованием метода DMRG (Density Matrix Renormalization Group), демонстрируют значительные отклонения от экспериментальной картины, особенно в области высоких энергий и волновых векторов, что указывает на превосходство используемого нами подхода в описании исследуемой системы.

Влияние и Перспективы: К Реалистичным Материалам

Предложенный подход формирует эталон для изучения взаимодействующих квантовых систем, находящихся в состоянии теплового равновесия. В рамках данной работы, удалось разработать методологию, позволяющую с высокой точностью описывать поведение сложных квантовых ансамблей при заданных температурах. Полученные результаты предоставляют надежную отправную точку для верификации других теоретических моделей и численных методов, используемых в квантовой статистической механике. Возможность сравнивать результаты, полученные различными способами, существенно ускоряет прогресс в понимании фундаментальных свойств материи и открывает новые перспективы для разработки передовых материалов с заданными свойствами. Данный подход, таким образом, играет ключевую роль в развитии теоретической физики конденсированного состояния и является важным шагом на пути к созданию реалистичных моделей сложных квантовых систем.

Применение периодических граничных условий позволило смоделировать систему, эквивалентную бесконечной, что значительно повысило реалистичность численных расчетов. В отличие от систем с жесткими границами, где краевые эффекты вносят искажения, периодические условия предполагают, что система повторяется в пространстве, устраняя необходимость в искусственных границах и связанных с ними артефактах. Такой подход особенно важен при изучении свойств материалов, где коллективное поведение большого числа частиц определяет макроскопические характеристики. Моделирование бесконечной системы позволяет более точно описать эти коллективные эффекты, приближая результаты к реальным физическим условиям и обеспечивая более надежную основу для теоретического анализа и предсказаний.

Полученные результаты открывают перспективы для исследования более сложных моделей и материалов, в частности, систем с наличием беспорядка или дальнодействующими взаимодействиями. Изучение подобных систем представляет значительный интерес для материаловедения и физики конденсированного состояния, поскольку позволяет приблизиться к моделированию реальных материалов, обладающих сложной структурой и свойствами. Возможность точного расчета характеристик относительно простых систем служит надежной основой для последующего анализа более сложных случаев, учитывающих влияние различных факторов, таких как дефекты кристаллической решетки или взаимодействие между удаленными частицами. Таким образом, данная работа является важным шагом на пути к созданию реалистичных моделей, способных адекватно описывать поведение сложных материалов в различных условиях.

Полученные в ходе расчетов собственные состояния демонстрируют высокую степень достоверности, оставаясь близкими к единице в низкоэнергетическом диапазоне. Этот результат свидетельствует о значительной точности использованных приближений и позволяет с уверенностью полагаться на полученные данные при дальнейшем изучении сложных квантовых систем. Высокая фидельность собственных состояний подтверждает, что выбранный метод адекватно описывает поведение системы в основном состоянии и возбужденных состояниях с низкой энергией, что крайне важно для прогнозирования ее физических свойств и разработки новых материалов с заданными характеристиками. Такая точность открывает перспективы для моделирования более реалистичных систем, включая материалы с дефектами и сложными взаимодействиями.

Исследование демонстрирует, что без чёткого определения температурного состояния системы, любое приближение к её характеристикам остаётся лишь шумом. Авторы предлагают метод построения состояния Гиббса, обходя ограничения традиционных методов тензорных сетей при низких температурах. Этот подход, основанный на использовании производственной спектральной функции и возбужденных состояний, позволяет с высокой точностью моделировать свойства квантовых спиновых цепей. Как отмечал Леонардо да Винчи: «Простота — высшая форма утонченности». В данном случае, элегантность метода заключается в его способности точно описывать сложные квантовые системы, используя лишь необходимые элементы и избегая избыточных вычислений. Чёткость определения задачи и математическая строгость алгоритма являются ключевыми факторами, обеспечивающими достоверность полученных результатов.

Что Дальше?

Представленный подход, позволяющий конструировать состояние Гиббса напрямую через производную спектральную функцию, безусловно, является шагом вперёд в преодолении ограничений методов тензорных сетей при низких температурах. Однако, наивная эйфория от кажущегося успеха была бы преждевременна. Доказательство корректности предложенной аппроксимации, а не просто демонстрация её работоспособности на тестовых примерах, остаётся открытым вопросом. Необходимо строго оценить погрешность, вносимую усечением пространства состояний, и установить границы применимости метода к системам с более сложной структурой.

Перспективным направлением представляется расширение данной техники на системы с более высокой размерностью и нетривиальной топологией. Возможно ли сохранить высокую точность аппроксимации при увеличении числа взаимодействующих степеней свободы? Или же мы столкнёмся с экспоненциальным ростом вычислительных затрат, делающим метод непрактичным для изучения реальных физических систем? Ответ на этот вопрос требует разработки более эффективных алгоритмов для вычисления производной спектральной функции и оптимизации параметров тензорных сетей.

В конечном счёте, истинная ценность данной работы заключается не столько в достигнутом прогрессе, сколько в постановке новых, более сложных вопросов. Ведь в физике, как и в математике, элегантность решения всегда уступает красоте правильно сформулированной проблемы.

---

Оригинал статьи: https://arxiv.org/pdf/2601.09326.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/