Упрощая сложное: Объединение методов снижения размерности и доменного разложения

---

В статье представлен обзор современных подходов к моделированию сложных систем, основанных на сочетании методов снижения размерности и доменного разложения для повышения эффективности вычислений.

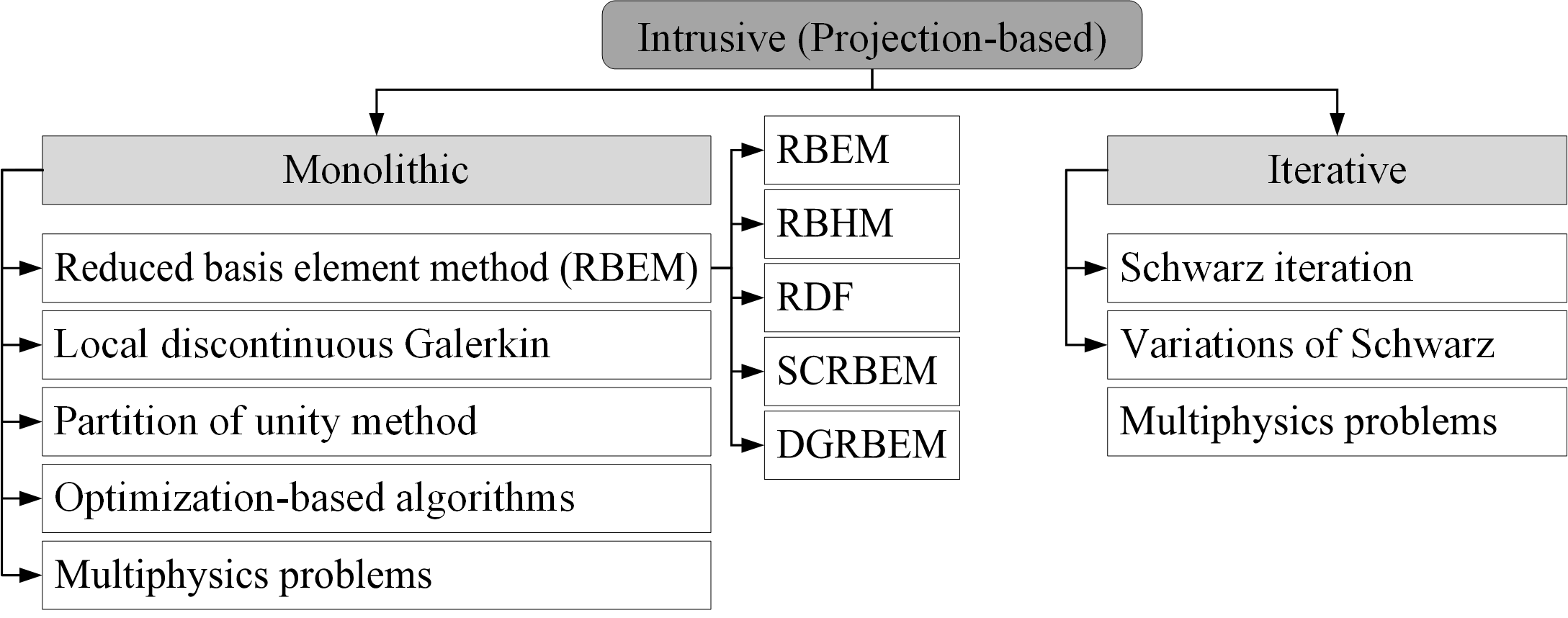
Обзор состояния и перспектив развития локальных методов снижения размерности, методов доменного разложения и алгоритмов неинтрузивной связи, включая машинное обучение.

Вычислительная гидродинамика (CFD), несмотря на свою точность, часто сталкивается с ограничениями по ресурсам при моделировании сложных инженерных систем. Данная работа, посвященная обзору ‘Introduction to the Combination of Reduced Order Models and Domain Decomposition: State of the Art and Perspectives’, рассматривает перспективное сочетание моделей пониженной размерности (ROM) и декомпозиции области (DD) для снижения вычислительных затрат. Анализ существующих методик, включающий как интрузивные, так и неинтрузивные подходы, выявляет тенденцию к использованию алгоритмов машинного обучения для эффективной реализации ROM в задачах с разветвленной геометрией. Какие новые возможности открываются для интеграции ROM и DD в промышленных приложениях и как можно преодолеть текущие ограничения в области сопряжения локальных моделей?

---

Преодолевая Проклятие Размерности: Вычислительные Вызовы Современного Моделирования

Многие задачи в науке и инженерии описываются с помощью уравнений в частных производных (УЧП) в многомерных пространствах, что порождает огромные вычислительные затраты. Это связано с тем, что сложность решения УЧП растет экспоненциально с увеличением числа размерностей, требуя все больше вычислительных ресурсов и времени. Например, моделирование турбулентности в гидродинамике или распространение тепла в сложных материалах часто требует решения УЧП в трех и более измерениях, что делает традиционные численные методы неэффективными. \frac{\partial u}{\partial t} = \nabla \cdot (k \nabla u) — типичное уравнение теплопроводности, сложность решения которого резко возрастает с увеличением размерности пространства, в котором происходит процесс. Таким образом, преодоление этих вычислительных ограничений является ключевой задачей для прогресса в различных областях науки и техники.

Традиционные численные методы, такие как метод конечных элементов, испытывают значительные трудности при увеличении размерности решаемой задачи. Это связано с тем, что вычислительная сложность и требуемая память растут экспоненциально с увеличением числа переменных. Например, для решения уравнения в двумерном пространстве требуется гораздо больше ресурсов, чем в одномерном, а переход к трехмерной задаче может сделать расчеты практически невозможными на современном оборудовании. Такой экспоненциальный рост обусловлен необходимостью дискретизации пространства и решения системы линейных уравнений, размер которой быстро увеличивается с ростом размерности. В результате, точные и своевременные симуляции сложных физических процессов, особенно в областях, требующих моделирования в высоких размерностях, становятся крайне затруднительными и требуют разработки новых, более эффективных алгоритмов.

Преодоление вычислительных ограничений, связанных с высокой размерностью, является ключевым фактором для прогресса в таких областях, как гидродинамика, материаловедение и климатология. В гидродинамике это позволяет моделировать турбулентные потоки с большей точностью, что необходимо для проектирования эффективных летательных аппаратов и оптимизации работы трубопроводов. В материаловедении, возможность проведения многомерных симуляций открывает путь к разработке новых материалов с заданными свойствами, например, сверхпроводников или легких и прочных композитов. И, наконец, в климатологии, точное моделирование сложных атмосферных процессов, учитывающих взаимодействие множества факторов в различных масштабах, имеет решающее значение для прогнозирования изменений климата и разработки стратегий адаптации. Таким образом, решение проблемы высокой размерности не только представляет собой вычислительный вызов, но и открывает новые возможности для научных открытий и технологических инноваций.

Модели Пониженной Размерности: Новый Подход к Сложным Системам

Модели пониженной размерности (МПП) представляют собой перспективный подход к преодолению проблемы «проклятия размерности», возникающей при моделировании сложных систем. Вместо работы с полным набором переменных, МПП аппроксимируют решение в подпространстве существенно меньшей размерности. Это достигается за счет идентификации наиболее значимых характеристик системы и проецирования исходной задачи на это подпространство, что значительно снижает вычислительные затраты и позволяет проводить анализ и предсказания в реальном времени, сохраняя при этом приемлемую точность. Эффективность МПП особенно заметна при моделировании задач, описываемых большим количеством степеней свободы, таких как задачи гидродинамики, теплопередачи и структурной механики.

Метод собственных ортогональных разложений (POD) используется для идентификации доминирующих мод в решениях полномасштабных задач и построения эффективных базисов пониженной размерности. В основе метода лежит анализ собственных значений и собственных векторов матрицы корреляции, полученной из данных полномасштабного моделирования. Доминирующие моды, соответствующие наибольшим собственным значениям, захватывают большую часть дисперсии данных и используются для построения базиса, который аппроксимирует исходное решение с значительно меньшим числом степеней свободы. Это позволяет существенно снизить вычислительные затраты при решении аналогичных задач или проведении параметрических исследований, сохраняя при этом приемлемую точность.

Применение метода собственных ортогональных разложений (POD) непосредственно к нелинейным задачам или задачам со сложной геометрией часто сталкивается с трудностями. Это связано с тем, что POD предполагает линейность и оптимально работает с данными, полученными из линейных систем. В нелинейных случаях, снимок решения, используемый для построения базиса POD, может не адекватно представлять все возможные режимы поведения системы. Для задач со сложной геометрией, получение достаточного количества снимков решения, необходимых для надежного построения базиса, может быть вычислительно затратным или практически невозможным. В таких ситуациях требуется использование более продвинутых методов, таких как нелинейные POD, динамические моды или адаптивные методы снижения размерности, чтобы эффективно снизить размерность модели и сохранить точность решения.

Метод Несвязных Галеркина и Доменное Разложение: Параллельные Вычисления для Сложных Задач

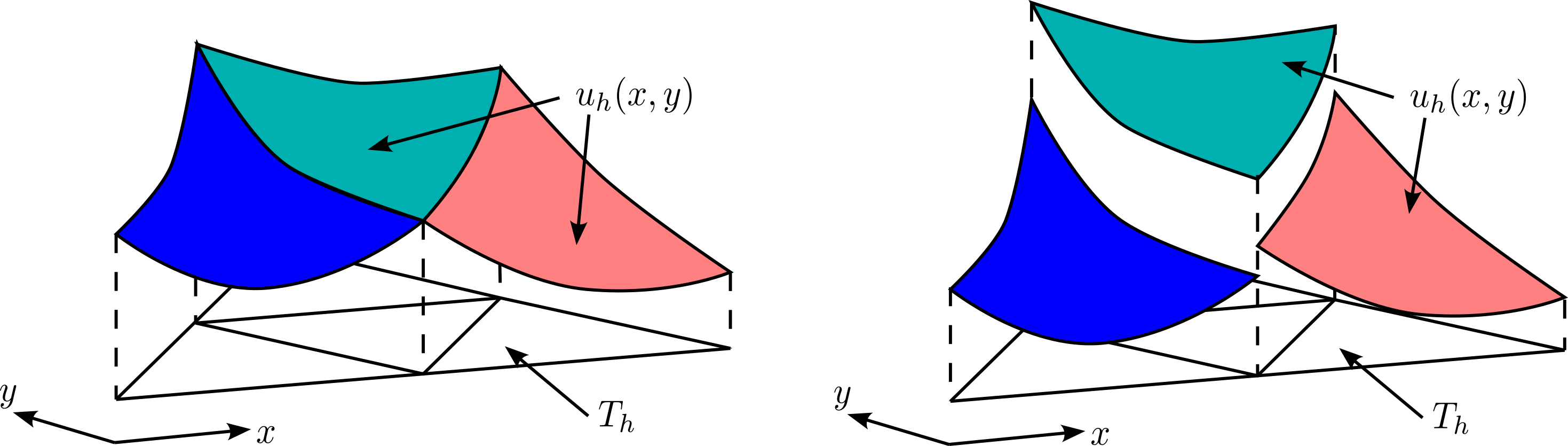
Метод несвязной аппроксимации Галеркина (DG) представляет собой численный подход к решению дифференциальных уравнений в частных производных (ДУЧП), обеспечивающий высокую точность аппроксимации, достигаемую за счет использования полиномиальных базисных функций высокой степени. В отличие от традиционных методов конечных элементов, DG не требует непрерывности решения между соседними элементами сетки, что особенно полезно при моделировании задач с разрывными решениями, таких как ударные волны или задачи с материальными неоднородностями. Гибкость DG также позволяет эффективно обрабатывать сложные геометрические области, поскольку не налагает жестких ограничений на форму элементов сетки, что упрощает построение сеток для объектов сложной формы. Порядок точности метода контролируется степенью полинома, используемого для аппроксимации решения в каждом элементе, позволяя достигать высокой точности с относительно небольшим количеством элементов сетки.

Сочетание метода Discontinuous Galerkin (DG) с методами доменного разложения, такими как метод Шварца, обеспечивает возможность распараллеливания вычислений и масштабируемость. Это достигается путем разбиения расчетной области на неперекрывающиеся поддомены, решение задачи на каждом поддомене независимо, и последующей итеративной передачи информации между поддоменами до достижения сходимости. Такая структура позволяет эффективно использовать многопроцессорные вычислительные системы и существенно сократить время решения задач, особенно для крупномасштабных симуляций с высокой степенью детализации. Выбор оптимального метода доменного разложения и стратегии обмена данными между поддоменами критически важен для достижения максимальной производительности и эффективности расчетов.

Гале́ркинская проекция является основополагающим компонентом в построении и анализе методов, таких как Discontinuous Galerkin (DG), обеспечивая стабильность и точность редуцированных моделей. Суть метода заключается в ортогональной проекции остаточной задачи на подпространство решений, что приводит к системе алгебраических уравнений, определяющих приближенное решение. Использование взвешенной нормы, основанной на функциях взвешивания, позволяет получить слабые формулировки уравнений, необходимые для обеспечения сходимости и устойчивости численных схем. Применение Гале́ркинской проекции гарантирует, что ошибка между точным и приближенным решением минимизируется в выбранной норме, что критически важно для получения надежных результатов при решении дифференциальных уравнений в частных производных, особенно в задачах с разрывными решениями или сложной геометрией.

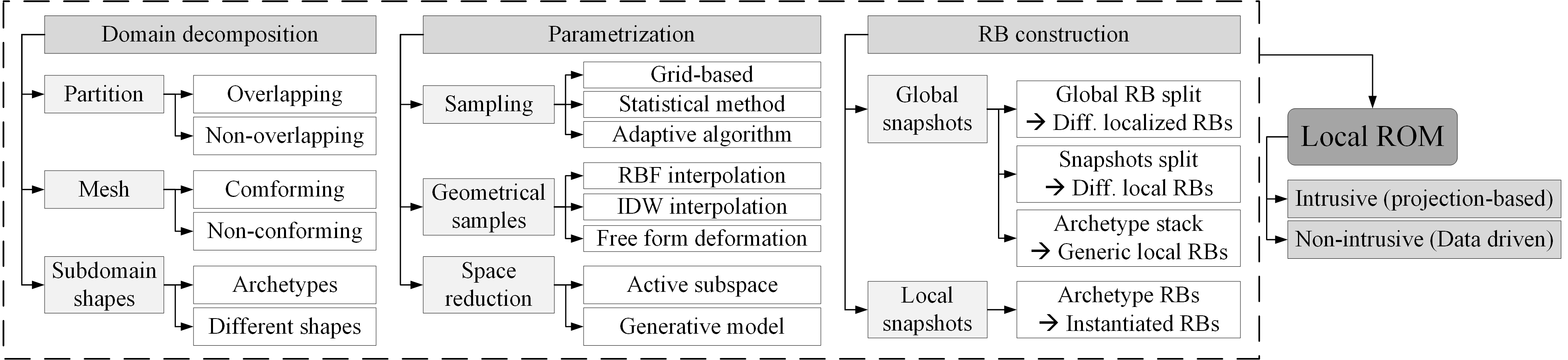
DGRBEM: Мощный и Универсальный Подход к Построению Моделей Пониженной Размерности

Метод Discontinuous Galerkin Reduced Basis Element Method (DGRBEM) представляет собой инновационный подход к построению Reduced Order Models (ROM), объединяющий в себе преимущества трех мощных численных методов. В его основе лежит метод Discontinuous Galerkin (DG), обеспечивающий высокую точность и гибкость при решении задач с разрывными решениями. Ключевым элементом является Reduced Basis (RB) метод, позволяющий значительно снизить вычислительные затраты за счет построения аппроксимации решения на подпространстве, сформированном на основе нескольких ключевых решений. Наконец, декомпозиция области определения задачи позволяет эффективно решать задачи большого масштаба, распределяя вычисления между несколькими процессорами. Синергия этих трех подходов позволяет DGRBEM успешно применяться для решения широкого спектра сложных задач, характеризующихся высокой размерностью и требующих высокой точности и эффективности.

Метод Discontinuous Galerkin Reduced Basis Element Method (DGRBEM) объединяет в себе сильные стороны нескольких подходов, что позволяет достичь значительного улучшения точности, масштабируемости и устойчивости при решении широкого спектра задач высокой размерности. В частности, применение Discontinuous Galerkin обеспечивает высокую точность аппроксимации, даже для задач с разрывными решениями, в то время как Reduced Basis Method эффективно снижает вычислительные затраты, используя предварительно вычисленные базисные функции. Дополнительно, использование декомпозиции области позволяет решать задачи, которые не помещаются в память одного вычислительного узла, тем самым расширяя область применимости метода к еще более сложным и масштабным проблемам. Такое сочетание преимуществ делает DGRBEM мощным инструментом для моделирования различных физических процессов и инженерных задач, требующих высокой точности и эффективности.

Для дальнейшей оптимизации точности и эффективности метода DGRBEM применяются различные усовершенствования. В частности, метод разделения единства (Partition of Unity Method) позволяет локально адаптировать базисные функции, улучшая аппроксимацию решения. Интеграция техник, таких как множители Лагранжа и обобщенное разложение (Proper Generalized Decomposition), способствует уменьшению размерности задачи и повышению устойчивости численных схем. Эти дополнения позволяют DGRBEM успешно решать сложные высокоразмерные задачи, сохраняя при этом высокую вычислительную эффективность и точность результатов, что делает его ценным инструментом в различных областях науки и техники.

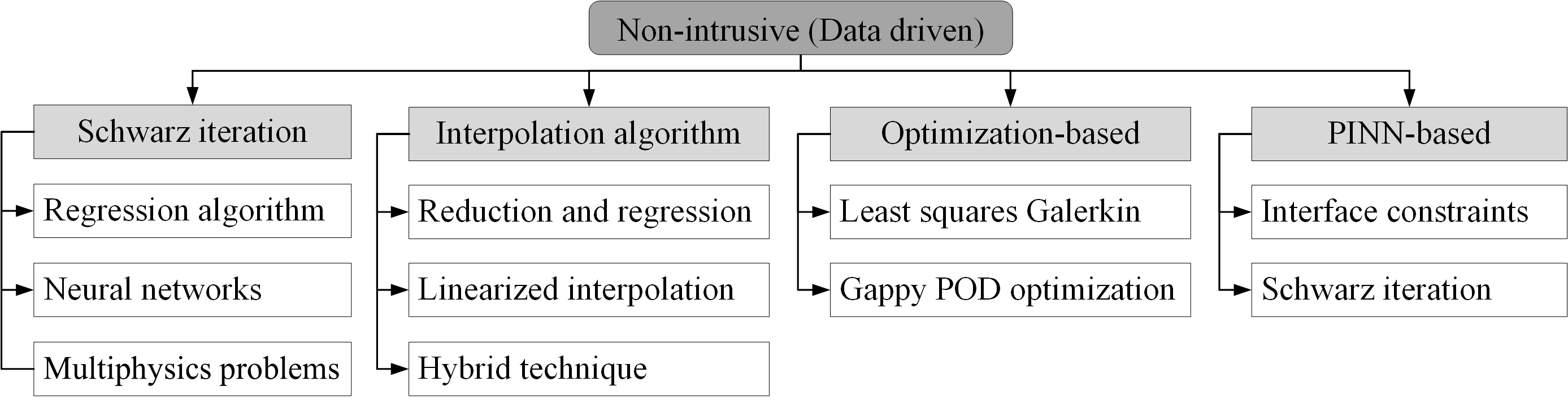
Будущее Моделирования: Модели Пониженной Размерности, Обученные на Данных

Искусственные нейронные сети (ИНС) представляют собой мощный инструмент для выявления сложных взаимосвязей и ускорения процессов моделирования, эффективно дополняя традиционные методы снижения порядка сложности (ROM). В отличие от ROM, которые опираются на априорные знания о физике системы, ИНС способны обучаться непосредственно на данных, выявляя неявные закономерности и приближения. Это особенно ценно в случаях, когда аналитическое описание системы затруднено или требует значительных вычислительных ресурсов. ИНС могут быть использованы для аппроксимации нелинейных функций, предсказания поведения системы в различных условиях и даже для создания суррогатных моделей, позволяющих значительно сократить время вычислений без существенной потери точности. Такое сочетание физически обоснованных моделей и методов машинного обучения открывает новые возможности для решения сложных научных и инженерных задач, требующих высокой точности и скорости расчетов.

Интеграция искусственных нейронных сетей (ИНС) в рамки моделей пониженной размерности (МПР) значительно повышает точность и эффективность прогнозирования, особенно в случаях, когда доступно ограниченное количество данных или присутствуют неопределенные параметры. Традиционные МПР часто сталкиваются с трудностями при экстраполяции за пределы обучающего набора данных или при учете нелинейных эффектов, которые сложно смоделировать аналитически. ИНС, благодаря своей способности к обучению сложным зависимостям на основе данных, способны компенсировать эти недостатки, позволяя создавать более робастные и точные модели. Например, ИНС могут быть использованы для аппроксимации нелинейных замыкающих соотношений или для коррекции ошибок, возникающих в результате упрощений, сделанных при построении МПР. В результате, комбинированный подход позволяет существенно ускорить вычислительные процессы, сохраняя при этом высокий уровень точности, что особенно важно для задач, требующих быстрого анализа и прогнозирования в условиях неопределенности.

Слияние физически обоснованного моделирования и подходов, основанных на данных, открывает принципиально новые горизонты для решения сложных научных и инженерных задач. Традиционные методы, опирающиеся на фундаментальные законы физики, зачастую сталкиваются с вычислительными ограничениями при моделировании систем высокой сложности. В то же время, методы машинного обучения, такие как искусственные нейронные сети, способны эффективно извлекать закономерности из больших объемов данных, но могут быть недостаточно точными при экстраполяции за пределы обучающей выборки. Комбинируя сильные стороны обоих подходов, исследователи создают гибридные модели, способные к быстрому и точному прогнозированию поведения сложных систем, что особенно важно в таких областях, как аэродинамика, климатология и материаловедение. Это позволяет не только оптимизировать существующие процессы, но и исследовать совершенно новые области, ранее недоступные для детального анализа, открывая путь к инновационным технологиям и научным открытиям.

Исследование методов понижения порядка моделирования, представленное в данной работе, акцентирует внимание на декомпозиции области и алгоритмах связывания. Особенный интерес представляет тенденция к использованию неинтрузивных подходов, в частности, машинного обучения, для повышения эффективности моделирования сложных систем. Это согласуется с глубокой убежденностью Вернера Гейзенберга: «Самое главное — не пытаться охватить необъятное, а сосредоточиться на принципиально важном». В контексте вычислительной математики, это означает, что вместо попыток точного моделирования всей системы, следует сконцентрироваться на выделении и эффективном представлении ее ключевых характеристик, что позволяет достичь приемлемого уровня точности при значительно меньших вычислительных затратах. Использование машинного обучения в неинтрузивных методах понижения порядка моделирования позволяет автоматизировать этот процесс выделения ключевых характеристик, приближая нас к элегантному и доказуемо корректному решению.

Что дальше?

Представленный обзор выявляет закономерную эволюцию методов снижения размерности. Переход от трудоёмких интрузивных подходов к неинтрузивным, опирающимся на машинное обучение, — не просто дань моде, но и логичный шаг к упрощению абстракций. Однако, следует признать, что «машинное обучение» зачастую служит лишь эвфемизмом для переноса вычислительной сложности из одной области в другую. Достаточно ли тщательно исследован вопрос устойчивости и обобщающей способности этих моделей при экстраполяции за пределы обучающей выборки?

Особого внимания заслуживает проблема эффективного связывания локальных моделей, полученных посредством декомпозиции области. Алгоритмы сопряжения, несмотря на кажущуюся элегантность, по-прежнему требуют тонкой настройки и чувствительны к выбору параметров. Каждый дополнительный параметр — это потенциальная точка отказа, а любое приближение — источник погрешности. Следует стремиться к минимизации избыточности, к алгоритмам, которые, подобно аксиомам, доказуемо гарантируют корректность результата.

В конечном счёте, истинный прогресс заключается не в увеличении вычислительной мощности, а в интеллектуальном упрощении моделей. Решение сложных задач должно быть элегантным и лаконичным, а не просто «работать на тестах». Будущие исследования должны быть направлены на разработку методов, которые позволяют не просто аппроксимировать реальность, но и понимать её фундаментальные принципы.

---

Оригинал статьи: https://arxiv.org/pdf/2601.09623.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/