Нейросети нового поколения: когда меньше значит больше

---

Исследование показывает, что сети Kolmogorov-Arnold способны превосходить многослойные персептроны по точности и эффективности вычислений, открывая новые возможности для задач с ограниченными ресурсами.

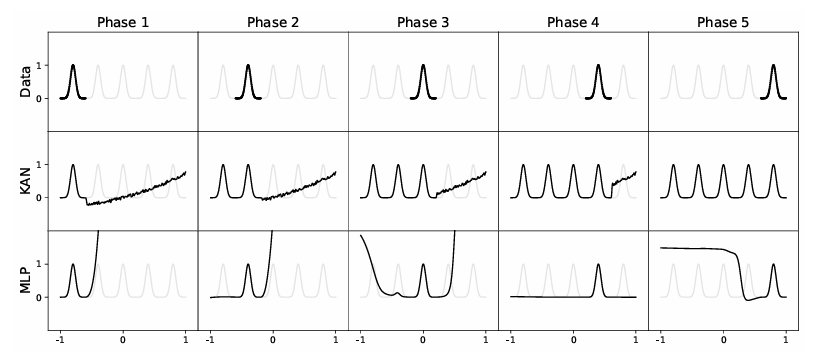
Компактные сети Kolmogorov-Arnold демонстрируют превосходство над многослойными персептронами в задачах аппроксимации функций и прогнозирования временных рядов, обеспечивая более высокую производительность при меньших вычислительных затратах.

Несмотря на широкое распространение многослойных персептронов (MLP), сохраняется потребность в нейронных сетях, обеспечивающих высокую точность при минимальных вычислительных затратах. В работе «Kolmogorov Arnold Networks и Multi-Layer Perceptrons: A Paradigm Shift in Neural Modelling» представлен сравнительный анализ KAN и MLP, демонстрирующий превосходство KAN в задачах аппроксимации функций, прогнозирования временных рядов и классификации. Полученные результаты указывают на то, что KAN надежно превосходят MLP по всем показателям, достигая большей предсказательной точности при значительно меньших вычислительных издержках. Способны ли KAN стать новой основой для разработки интеллектуальных систем, требующих как высокой производительности, так и интерпретируемости?

---

Сложность Аппроксимации Функций: Вызов для Современных Алгоритмов

Традиционные методы, такие как многослойные персептроны (MLP), несмотря на свою универсальность, сталкиваются с существенными вычислительными трудностями при аппроксимации сложных функций. По мере увеличения размерности входных данных потребность в параметрах модели растет экспоненциально, что приводит к значительному увеличению времени обучения и вычислительных затрат. Это особенно заметно в задачах, требующих высокой точности, где для адекватного представления функции необходимы модели с огромным количеством весов. Например, в задачах оценки куба (cube estimation) MLP демонстрируют среднюю квадратичную ошибку (MSE) в 2599.5886, что значительно превышает показатель KAN, достигающий всего 15.2706. Таким образом, эффективная аппроксимация сложных функций остается сложной задачей для классических методов, требующей поиска альтернативных подходов.

По мере увеличения размерности входных данных количество параметров в многослойных персептронах (MLP) растёт экспоненциально. Это приводит к значительному увеличению вычислительной сложности и потребности в памяти, делая обучение модели крайне затруднительным и неэффективным. Увеличение числа параметров не только замедляет процесс обучения, но и повышает риск переобучения, особенно при ограниченном объеме обучающих данных. В результате, модели становятся менее обобщающими и демонстрируют низкую производительность на новых, ранее не виденных данных. Данная проблема особенно актуальна в задачах, требующих высокой точности аппроксимации сложных функций, где даже небольшое увеличение размерности может привести к неприемлемому росту вычислительных затрат и снижению эффективности модели.

Ограничения в точности аппроксимации функций, проявляющиеся при использовании традиционных многослойных персептронов (MLP), существенно влияют на прикладные задачи, требующие высокой точности, такие как прогнозирование временных рядов и построение моделей данных. Например, при оценке функции в многомерном пространстве (cube estimation) MLP демонстрируют среднеквадратичную ошибку (MSE) в 2599.5886, что значительно превышает результат, достигнутый альтернативным подходом KAN, где MSE составляет всего 15.2706. Данное различие подчеркивает необходимость разработки более эффективных методов аппроксимации, способных обеспечить необходимую точность для решения сложных задач моделирования и анализа данных.

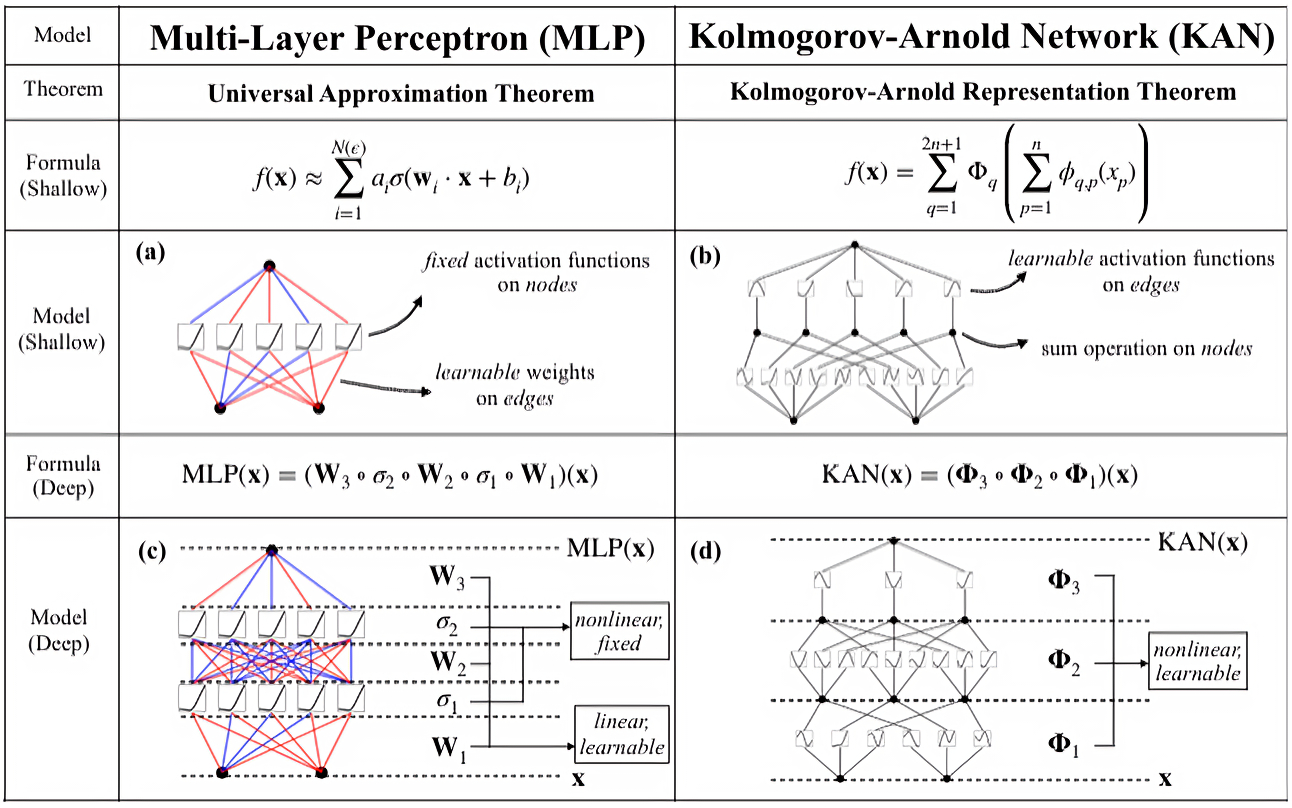
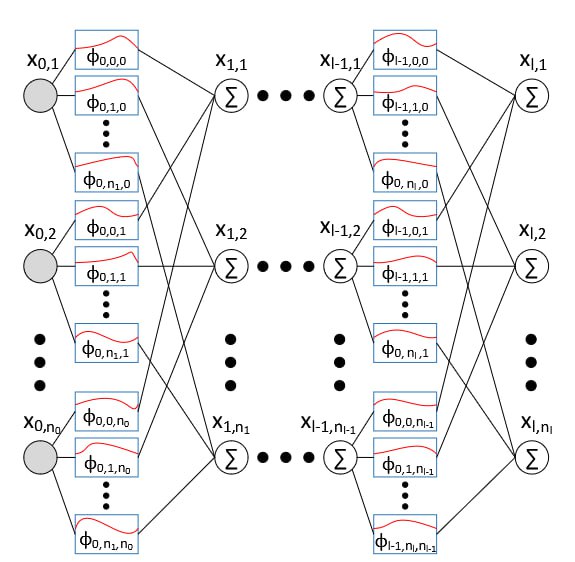
Архитектура KAN: Сплайны как Основа Эффективного Решения

Архитектура KAN использует теорему Колмогорова для разложения сложных многомерных функций на более простые одномерные функции. В основе этого подхода лежит возможность представления любой непрерывной функции как комбинации одномерных функций, определенных на некотором множестве. Теорема Колмогорова гарантирует существование такого разложения, что позволяет снизить вычислительную сложность и количество параметров, необходимых для моделирования сложных зависимостей. Разложение происходит путем последовательного применения одномерных функций к каждой переменной, что позволяет обрабатывать входные данные поэтапно и эффективно. Данный метод обеспечивает более компактное представление функции по сравнению с традиционными подходами, требующими моделирования всей функции как единого целого.

В архитектуре KAN для представления унивариантных компонентов используются сплайн-активации, параметризуемые для достижения требуемой точности. Сплайны позволяют аппроксимировать функции с высокой степенью гибкости, адаптируясь к различным формам и особенностям данных. Параметризация сплайнов включает в себя контроль над узлами, порядком и другими характеристиками, что позволяет точно настроить функцию активации для конкретной задачи и оптимизировать баланс между сложностью модели и ее способностью к обобщению. Такой подход обеспечивает эффективное представление данных с меньшим количеством параметров по сравнению с традиционными методами, что способствует ускорению обучения и повышению производительности модели.

Архитектура KAN демонстрирует значительное снижение количества параметров по сравнению с традиционными методами, что способствует улучшению обучения и обобщающей способности модели. В задаче оценки квадратичной функции KAN достигает среднеквадратичной ошибки (MSE) в 0.1743, что на 80.49% ниже, чем у многослойного персептрона (MLP) со значением MSE 0.8938. Это снижение числа параметров позволяет KAN более эффективно использовать вычислительные ресурсы и избегать переобучения, особенно при работе с ограниченными объемами данных.

Техника расширения сетки (Grid Extension) является ключевым элементом архитектуры KAN, обеспечивающим обработку входных данных, выходящих за пределы первоначально определенного диапазона. В процессе обучения и эксплуатации, значения входных параметров могут превышать границы, установленные при инициализации сплайновой сетки. Для решения этой проблемы, техника динамически расширяет сетку, добавляя узлы и пересчитывая коэффициенты сплайнов за пределами исходного диапазона. Это позволяет модели корректно обрабатывать новые, ранее не встречавшиеся значения входных данных без потери точности и необходимости переобучения, сохраняя эффективность и обобщающую способность архитектуры KAN.

Эмпирическое Подтверждение: Производительность KAN в Различных Приложениях

Оценка KAN на наборах данных «Square Numbers» и «Numbers» продемонстрировала его превосходство в задачах аппроксимации функций, что было количественно оценено с помощью среднеквадратичной ошибки (MSE). В ходе экспериментов KAN показал более низкие значения MSE по сравнению с традиционными методами, подтверждая его способность к более точной аппроксимации сложных функциональных зависимостей. Полученные результаты свидетельствуют о высокой эффективности KAN в решении задач, требующих точного моделирования и прогнозирования на основе числовых данных.

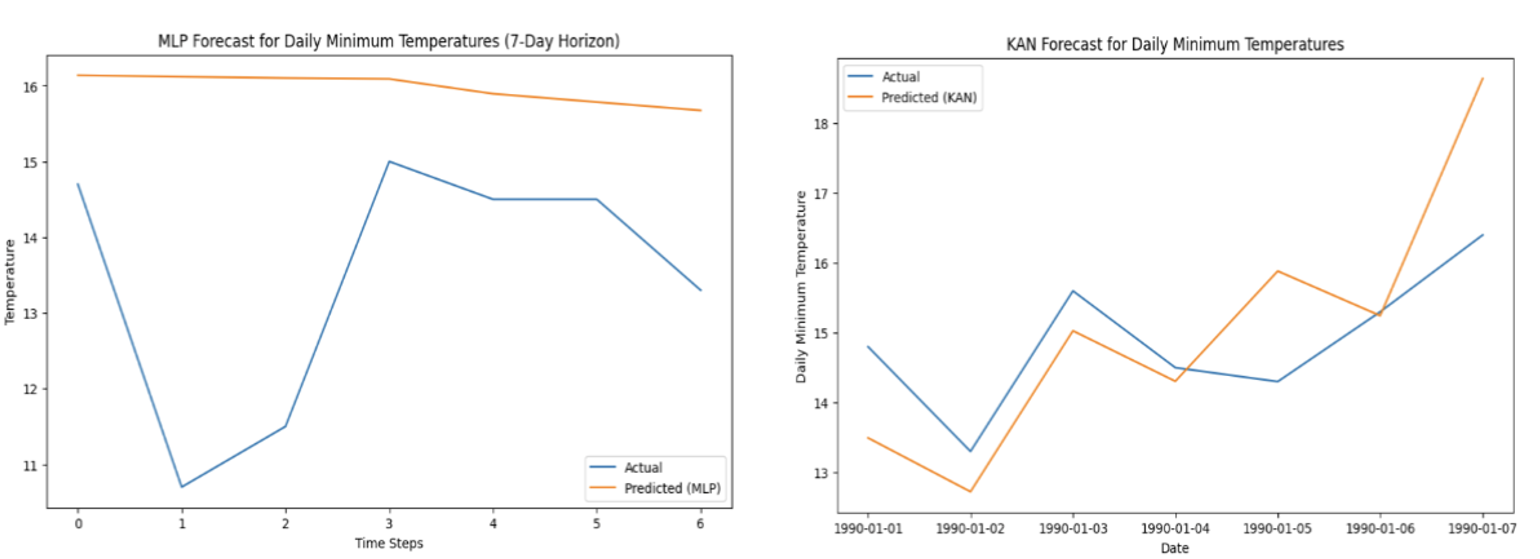
При прогнозировании временных рядов, на основе набора данных о ежедневных минимальных температурах, KAN демонстрирует сопоставимую или улучшенную точность при меньших вычислительных затратах. В частности, средняя квадратичная ошибка (MSE) KAN составляет 1.4201, что на 79.87% ниже, чем у многослойного персептрона (MLP), значение MSE которого равно 7.0565. Данный результат указывает на более эффективное использование вычислительных ресурсов KAN при решении задач прогнозирования временных рядов.

При валидации архитектуры KAN на наборе данных Wine, она продемонстрировала высокую точность классификации, достигнув 98.43%. Этот результат на 2.21% превышает точность, показанную многослойным персептроном (MLP), который достиг 96.30% на том же наборе данных. Достижение высокой точности при одновременном снижении сложности модели подтверждает эффективность KAN в задачах классификации.

Эффективность KAN с точки зрения вычислительных затрат подтверждена измерениями операций с плавающей точкой (FLOPs) с использованием алгоритма Де Бура. Результаты демонстрируют значительное снижение вычислительной нагрузки по сравнению с многослойными персептронами (MLP). В частности, для оценки куба KAN обеспечивает снижение FLOPs на 99%, а для оценки квадрата — на 99.71%. Данные показатели свидетельствуют о потенциале KAN для реализации высокопроизводительных вычислений в задачах, требующих интенсивной обработки данных.

Влияние и Перспективы: Эффективный Искусственный Интеллект Будущего

Архитектура KAN представляет собой перспективный подход к созданию энергоэффективных систем искусственного интеллекта, что особенно важно для развертывания на устройствах с ограниченными ресурсами. В отличие от традиционных нейронных сетей, требующих огромного количества параметров и вычислительных мощностей, KAN использует сплайн-активации, позволяющие представлять сложные функции с существенно меньшим количеством параметров. Это не только снижает энергопотребление, но и открывает возможности для создания компактных моделей, пригодных для встраиваемых систем, мобильных устройств и периферийных вычислений. В условиях растущей потребности в интеллектуальных решениях, работающих на ограниченных ресурсах, разработка подобных энергоэффективных архитектур становится ключевым фактором для широкого внедрения искусственного интеллекта в повседневную жизнь.

Возможность компактного представления сложных функций с использованием меньшего числа параметров открывает значительные перспективы для сжатия моделей искусственного интеллекта и их развертывания на периферийных устройствах. Традиционные нейронные сети часто требуют огромного количества параметров, что затрудняет их использование на устройствах с ограниченными вычислительными ресурсами и энергопотреблением. Архитектура KAN, благодаря своей эффективности, позволяет существенно уменьшить размер модели без значительной потери точности. Это особенно важно для приложений, требующих обработки данных в реальном времени непосредственно на устройствах, таких как смартфоны, беспилотные летательные аппараты или носимые датчики. Сжатие моделей не только снижает требования к памяти и вычислительной мощности, но и ускоряет процесс инференса, что критически важно для оперативного принятия решений в различных сценариях применения.

Дальнейшие исследования сосредоточены на изучении масштабируемости архитектуры KAN для работы с данными еще большей размерности и решения более сложных задач. Поскольку современные наборы данных и алгоритмы машинного обучения становятся все более требовательными к вычислительным ресурсам, способность KAN эффективно представлять сложные функции с меньшим количеством параметров становится особенно ценной. Планируется провести эксперименты с различными типами высокоразмерных данных, включая изображения высокого разрешения, видео и сложные научные симуляции, чтобы оценить, как KAN сохраняет свою эффективность при увеличении масштаба. Кроме того, исследования направлены на адаптацию KAN к более сложным задачам, таким как обработка естественного языка и автономная навигация, что потребует разработки новых методов обучения и оптимизации для поддержания высокой производительности и энергоэффективности.

Исследования показывают, что расширение использования сплайн-активаций за пределы архитектуры KAN может привести к значительному повышению эффективности и производительности нейронных сетей. В отличие от традиционных активаций, таких как ReLU или sigmoid, сплайны позволяют более точно аппроксимировать сложные функции с меньшим количеством параметров, что ведет к снижению вычислительной нагрузки и энергопотребления. Внедрение сплайн-активаций в существующие архитектуры, такие как сверточные или рекуррентные сети, потенциально может уменьшить размер моделей без существенной потери точности, делая их более подходящими для развертывания на устройствах с ограниченными ресурсами и в приложениях, требующих высокой скорости обработки данных. Дальнейшие исследования в этой области направлены на оптимизацию методов обучения сплайн-активаций и адаптацию их к различным типам данных и задач машинного обучения.

Представленное исследование демонстрирует, что сети Колмогорова-Арнольда (KAN) предлагают значительное улучшение вычислительной эффективности по сравнению с многослойными персептронами (MLP). Это особенно важно, учитывая, что, согласно принципам математической чистоты, любой алгоритм должен быть доказуем, а не просто эмпирически подтвержден. Как заметила Барбара Лисков: «Программы должны быть спроектированы так, чтобы изменения в одной части не влияли на другие». Этот принцип напрямую применим к KAN, чья архитектура обеспечивает большую модульность и предсказуемость, что способствует повышению надежности и упрощает отладку. Эффективность KAN в задачах аппроксимации функций и прогнозирования временных рядов подтверждает их потенциал для ресурсоограниченных приложений, где каждое вычислительное действие имеет значение.

Что Дальше?

Представленные результаты, безусловно, демонстрируют превосходство сетей Колмогорова-Арнольда над традиционными многослойными перцептронами в определенных задачах. Однако, пусть N стремится к бесконечности — что останется устойчивым? Простое снижение вычислительных затрат не является самоцелью. Необходимо критически оценить, насколько хорошо эти сети масштабируются на действительно сложных, высокоразмерных данных, где количество параметров, необходимых для адекватного представления функции, может экспоненциально возрастать. Очевидно, что выигрыш в FLOPs теряет смысл, если для достижения приемлемой точности требуется экспоненциально больше слоев.

Ключевым вопросом остается доказательство универсальной аппроксимации для KANs в более общих функциональных пространствах. Теорема Колмогорова гарантирует существование функции, представимой с заданной точностью, но не указывает конкретный алгоритм её построения. Необходимо разработать эффективные методы обучения этих сетей, избегая проблем переобучения и локальных минимумов, которые неизбежно возникают при работе с высокоразмерными пространствами. Простое увеличение количества нейронов не является решением.

В конечном счете, истинная ценность KANs заключается не в достижении лучших результатов на текущих бенчмарках, а в возможности построения более элегантных и интерпретируемых моделей. Отказ от избыточных параметров и стремление к математической чистоте — вот что действительно может привести к прорыву в области машинного обучения. Будущее за алгоритмами, которые можно доказать, а не просто протестировать.

---

Оригинал статьи: https://arxiv.org/pdf/2601.10563.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/