Оптимальное кодирование в нейронных сетях: новый взгляд

---

Исследование показывает, что широкий спектр задач нейронного кодирования можно эффективно решать, используя методы выпуклой оптимизации.

Предложен подход, позволяющий аналитически изучать нейронные представления и функции через оптимизацию матриц сходства.

Нейронные сети, несмотря на свою мощь, часто представляются как «черные ящики», затрудняя понимание принципов кодирования информации. В работе ‘Convex Efficient Coding’ предложен новый подход к анализу нейронных кодов, основанный на оптимизации матрицы репрезентативного сходства. Показано, что широкий класс задач нейронного кодирования может быть сформулирован как задача выпуклой оптимизации, что позволяет получить аналитические решения и доказать новые свойства, такие как однозначная идентификация параметров модели и объяснение различий в кодировании в ретине и коре головного мозга. Какие еще фундаментальные принципы нейронного кодирования можно выявить, используя инструменты выпуклой оптимизации?

---

Шёпот Мозга: Эффективность в Кодировании Информации

Понимание того, как мозг эффективно кодирует информацию, является центральной задачей нейронауки, однако традиционные методы часто оказываются неспособны уловить лежащие в основе этого процесса принципы. Исследования показывают, что мозг не стремится к максимальной детализации при представлении данных, а скорее оптимизирует процесс, используя минимально необходимое количество нейронов для передачи важной информации. Это связано с тем, что поддержание активности большого числа нейронов требует значительных энергетических затрат, что невыгодно для организма. Поэтому, нейробиологи все чаще обращаются к новым подходам, таким как анализ паттернов активности небольших групп нейронов и изучение механизмов, лежащих в основе формирования разреженных представлений, чтобы приблизиться к пониманию истинных принципов кодирования информации в мозге.

Нервная система, стремясь к максимальной эффективности, использует принципы экономии энергии при кодировании информации. Исследования показывают, что мозг отдает предпочтение “разрешенным” представлениям, когда лишь небольшое количество нейронов активно реагирует на конкретный стимул. Такой подход позволяет снизить метаболическую нагрузку и оптимизировать использование ресурсов. Вместо того, чтобы активировать все доступные нейроны, мозг выбирает наиболее информативные, что значительно уменьшает энергозатраты и повышает скорость обработки данных. Этот принцип “меньше — значит лучше” играет ключевую роль в обеспечении быстрого и надежного восприятия окружающего мира, а также в формировании сложных когнитивных функций.

Поиск эффективности в обработке информации мозгом усложняется необходимостью декодирования сложных сенсорных данных из зашумленных нейронных сигналов. Нейроны не передают информацию идеально; на их активность влияют внутренний шум и внешние помехи. Следовательно, мозг вынужден решать задачу извлечения значимой информации из этого хаоса, что требует сложных механизмов фильтрации и обработки. Эффективное декодирование предполагает не только распознавание сигнала, но и подавление шума, а также адаптацию к меняющимся условиям окружающей среды. Этот процесс представляет собой серьезную вычислительную задачу, требующую оптимального баланса между точностью и энергоэффективностью, что делает понимание принципов декодирования ключевым для раскрытия механизмов работы мозга.

Аффинные Автокодировщики: Биологически Правдоподобная Модель

Аффинные автокодеры представляют собой перспективную основу для моделирования нейронных представлений благодаря использованию аффинных преобразований. В отличие от нелинейных моделей, аффинные преобразования, описываемые как f(x) = Wx + b, где W — матрица весов, а b — вектор смещения, более точно отражают динамику биологических нейронных сетей. Биологические нейроны часто суммируют взвешенные входы и добавляют смещение перед активацией, что функционально эквивалентно аффинному преобразованию. Использование аффинных преобразований позволяет создавать более реалистичные и интерпретируемые модели нейронных процессов, упрощая анализ и понимание работы мозга.

Автокодировщики, в процессе обучения, способны формировать сжатые и эффективные представления входных данных, следуя принципу минимизации избыточности. Этот процесс достигается за счет обучения сети выделять наиболее значимые признаки, отбрасывая несущественные детали, что приводит к уменьшению размерности данных без существенной потери информации. В результате, закодированное представление данных содержит только необходимую информацию для реконструкции исходного сигнала, обеспечивая эффективное использование ресурсов и повышая устойчивость к шуму. Подобный подход позволяет значительно сократить объем данных, необходимых для хранения и обработки, что особенно важно для задач, связанных с ограниченными вычислительными ресурсами или большим объемом данных.

Включение положительного ограничения в архитектуру автоэнкодеров обеспечивает биологическую правдоподобность полученных признаков, поскольку отражает неотрицательность нейронных сигналов. Биологические нейроны, как правило, активируются только при получении положительных входных сигналов и не передают отрицательные значения. Ограничение весов и активаций автоэнкодера положительными значениями моделирует это поведение, что позволяет сети обучаться представлениям, которые более соответствуют принципам функционирования биологических нейронных сетей. Это ограничение способствует формированию более реалистичных и интерпретируемых признаков, что особенно важно для применения автоэнкодеров в нейробиологических исследованиях и моделировании.

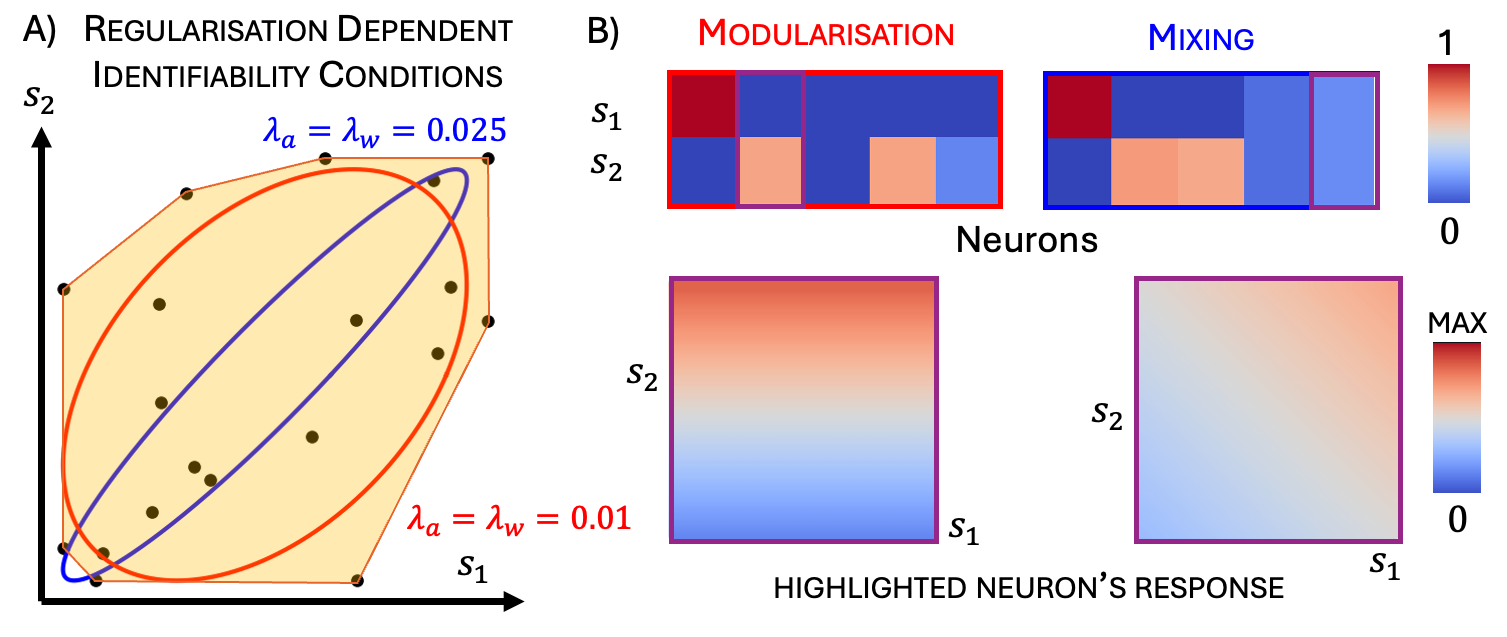
Идентифицируемость и Условие Плотного Рассеяния

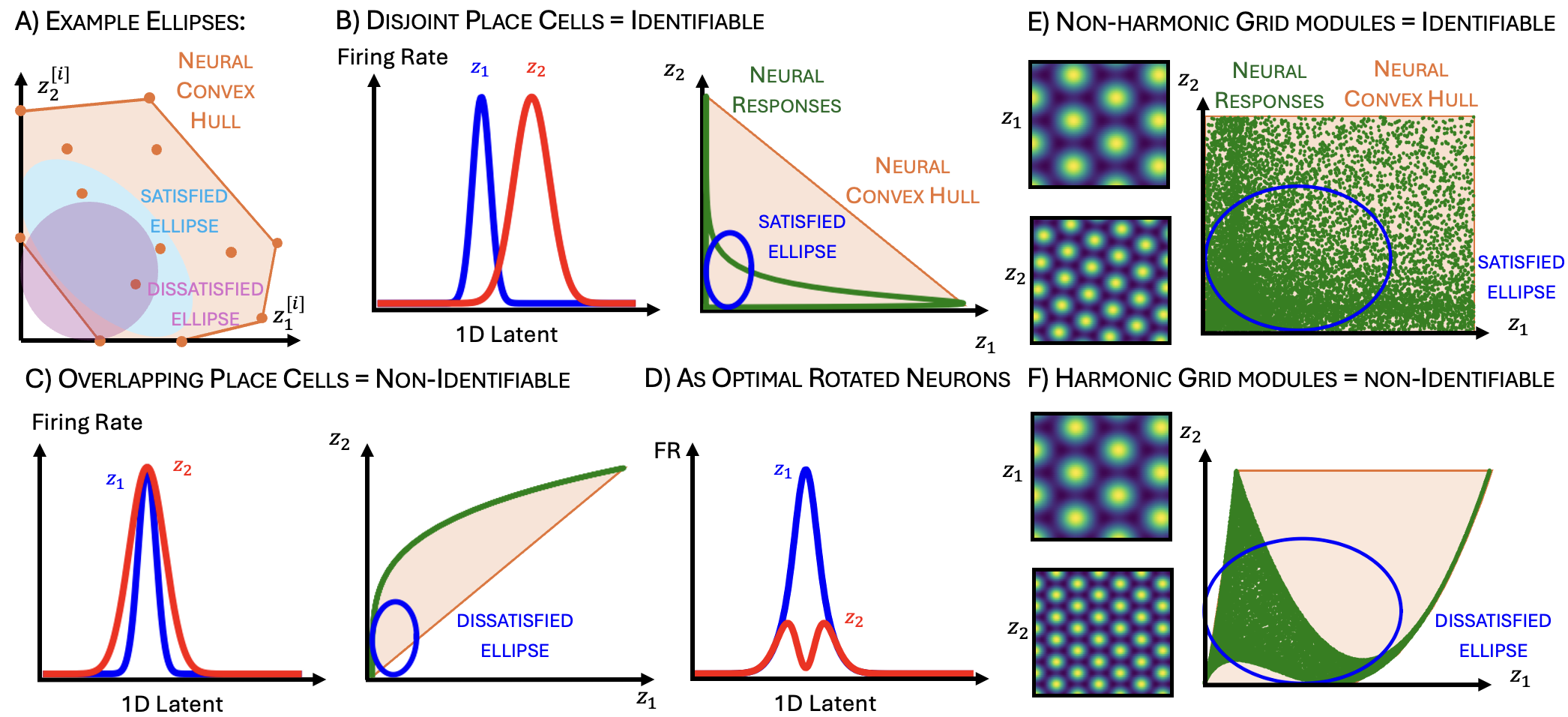
При использовании автоэнкодеров для нейронного моделирования важной проблемой является обеспечение однозначности (идентифицируемости) полученного представления на основе наблюдаемых данных. Неоднозначность возникает, когда различные скрытые представления могут приводить к одинаковым выходным данным, что затрудняет интерпретацию и надежность модели. Гарантия идентифицируемости необходима для того, чтобы из наблюдаемых данных можно было однозначно восстановить скрытое представление, что критически важно для корректной работы и интерпретации нейронных моделей, построенных на основе автоэнкодеров. Отсутствие идентифицируемости приводит к непредсказуемым результатам и затрудняет проверку адекватности модели.

Для обеспечения идентифицируемости, то есть уникального определения представлений, полученных с помощью автоэнкодеров, могут применяться методы выпуклой оптимизации. Выпуклость целевой функции гарантирует, что локальный минимум является также глобальным, что обеспечивает надежное и однозначное декодирование нейронных представлений. Использование выпуклых оптимизационных алгоритмов позволяет избежать неоднозначности в процессе реконструкции сигнала и, следовательно, обеспечивает стабильность и предсказуемость результатов моделирования нейронных сетей. Применение этих методов особенно важно в задачах, где требуется точное восстановление исходных данных из сжатого представления, например, при анализе активности нейронов или обработке изображений.

Условие “плотного рассеяния” (tight scattering condition) предоставляет математическую гарантию идентифицируемости неотрицательного аффинного автоэнкодера. Это достигается путем установления выпуклости семейства задач, включающих линейные/аффинные сети и неотрицательное кодирование. Выпуклость гарантирует, что решение задачи оптимизации, находящееся в локальном минимуме, также является глобальным минимумом, обеспечивая однозначное восстановление входных данных. Доказательство идентифицируемости опирается на анализ матрицы рассеяния Σ, характеризующей взаимосвязь между входными и выходными сигналами автоэнкодера, и требует выполнения определенных условий на ее элементы для обеспечения выпуклости целевой функции.

Данная теоретическая модель позволяет аналитически определить порог разреженности, который определяет переход между ON-OFF кодированием и кодированием по одному каналу в нейронах сетчатки. Этот порог, определяемый математически, указывает критическое значение, при котором активность нейрона переходит от кодирования информации посредством разности между сигналами «включено» и «выключено» к кодированию, основанному исключительно на интенсивности сигнала по одному конкретному каналу. T_{sparsity} представляет собой величину, определяющую эту границу, и может быть рассчитан на основе параметров сети и характеристик входных данных, обеспечивая количественную оценку перехода между различными режимами кодирования в сетчатке.

Декодирование и Валидация Нейронных Представлений

Матрицы сходства представлений RSM представляют собой эффективный инструмент для количественной оценки схожести нейронных представлений, полученных с помощью аффинного автокодировщика. Суть метода заключается в сопоставлении паттернов активации нейронов при предъявлении различных стимулов. Чем ближе векторы активации для двух стимулов, тем более похожи их представления в нейронной сети, и тем выше значение соответствующего элемента в RSM. По сути, RSM преобразует сложное пространство нейронных активаций в матрицу расстояний, позволяя наглядно визуализировать и сравнивать, как различные стимулы кодируются в нейронной сети. Этот подход позволяет не только оценить качество обучения модели, но и выявить, какие признаки наиболее важны для формирования представлений, а также понять, как различные части нейронной сети участвуют в кодировании информации.

Для проверки соответствия модели аффинного автокодировщика реальной биологической активности исследователи используют матрицы сходства представлений (РСМ). Эти матрицы, рассчитанные как для данных, полученных от нейронных сетей, так и от фактической нейронной активности, позволяют количественно оценить, насколько хорошо модель воспроизводит закономерности, наблюдаемые в мозге. Сравнение РСМ позволяет выявить соответствия и расхождения между смоделированными и реальными представлениями, подтверждая или опровергая способность модели улавливать биологически релевантные паттерны обработки информации. Высокая степень корреляции между РСМ, полученными из модели и реальных нейронных данных, служит убедительным доказательством того, что модель способна эффективно аппроксимировать принципы работы мозга.

Включение модульных представлений, при котором различные популяции нейронов кодируют отдельные признаки, значительно повышает возможность однозначной идентификации и биологическую правдоподобность модели. Этот подход имитирует организацию реальных нейронных сетей, где специализированные группы нейронов отвечают за обработку конкретных аспектов информации, таких как цвет, форма или движение. Использование модульных представлений позволяет более эффективно декодировать нейронные сигналы и сопоставлять их с конкретными признаками, что подтверждается сравнением матриц репрезентативного сходства, полученных из модели и реальных нейронных данных. Такой подход не только улучшает точность моделирования, но и способствует лучшему пониманию принципов организации и функционирования биологических нейронных сетей.

Будущие Направления: К Эффективным Интерфейсам Мозг-Компьютер

Перспективные исследования в области создания эффективных интерфейсов мозг-компьютер направлены на интеграцию биологически обоснованных ограничений в структуру аффинных автокодеров. В частности, учёные стремятся моделировать присущие мозгу принципы разреженности — когда лишь небольшая часть нейронов активна в любой момент времени — и локальной связности, подразумевающей, что нейроны взаимодействуют преимущественно со своими ближайшими соседями. Внедрение этих ограничений позволит создавать более реалистичные и энергоэффективные модели нейронной активности, что, в свою очередь, значительно улучшит производительность и надёжность будущих систем управления устройствами силой мысли и восстановления утраченных функций. Такой подход не только повысит точность декодирования намерений пользователя, но и снизит вычислительную нагрузку, необходимую для обработки сигналов мозга.

Неотрицательная матричная факторизация (НМФ) представляет собой мощный вычислительный инструмент для создания разреженных и эффективных представлений нейронных данных. В отличие от традиционных методов, которые могут генерировать сложные и избыточные векторы активации, НМФ гарантирует, что все элементы полученных матриц будут неотрицательными. Это свойство особенно ценно при анализе данных головного мозга, поскольку биологические нейронные сигналы по своей природе не могут быть отрицательными. Применяя НМФ, исследователи могут выявлять основные компоненты, которые представляют собой значимые паттерны активности, и одновременно уменьшать размерность данных, упрощая последующий анализ и повышая эффективность алгоритмов обработки сигналов мозга. Такой подход позволяет извлекать наиболее релевантную информацию из сложных нейронных данных, что крайне важно для разработки усовершенствованных интерфейсов мозг-компьютер.

Сочетание передовых вычислительных методов и современных нейровизуализационных технологий открывает принципиально новые возможности для изучения мозга и создания эффективных интерфейсов мозг-компьютер. Интеграция таких подходов, как аффинные автокодеры и факторизация неотрицательной матрицы, с данными, полученными с помощью функциональной магнитно-резонансной томографии (фМРТ) или электроэнцефалографии (ЭЭГ), позволяет не только декодировать нейронные сигналы с высокой точностью, но и получить более глубокое понимание принципов организации и функционирования мозга. Такое синергетическое взаимодействие способствует разработке интерфейсов, способных не только восстанавливать утраченные функции, но и расширять когнитивные возможности человека, открывая перспективы в области нейропротезирования, реабилитации и нейроуправления.

Статья убедительно демонстрирует, что даже сложные задачи нейронного кодирования могут быть сведены к изящным формулам выпуклой оптимизации. По сути, авторы не ищут истину в данных, а уговаривают их проявить благосклонность, представляя задачу в удобном свете. Это напоминает о словах Стивена Хокинга: «Интеллект — это способность адаптироваться к обстоятельствам». Здесь адаптация заключается в переформулировке проблемы, чтобы получить желаемое решение. Идея о работе с матрицами репрезентативного сходства, как с ключом к пониманию нейронных представлений, лишь подтверждает, что любая модель — это заклинание, работающее до первого столкновения с реальностью, то есть, с продакшеном.

Что дальше?

Представленные построения, переводящие задачи нейронного кодирования в область выпуклой оптимизации, конечно, льстят разуму. Однако не стоит полагать, что заклинание сработает безупречно. Реальные данные — это не гладкие матрицы сходства, а хаотичные шёпоты, полные шума и артефактов. Уравнения, прекрасные на бумаге, столкнутся с жестокой реальностью продакшена, где даже незначительное отклонение от идеала может разрушить всю конструкцию.

Попытки отождествить полученные решения с биологической реальностью требуют особой осторожности. Не следует забывать, что мозг — это не оптимизатор, а скорее алхимик, смешивающий случайность и необходимость. Задача состоит не в том, чтобы найти «правильное» представление, а в том, чтобы понять, как эти неидеальные представления возникают и функционируют в условиях постоянного шума и ограничений. Следующим шагом видится разработка методов, позволяющих оценивать устойчивость полученных решений к возмущениям и неполноте данных — ведь чистые данные, как известно, это миф, придуманный менеджерами.

Очевидно, что границы применимости предложенного подхода нуждаются в дальнейшей проверке. Возможно ли расширить его на более сложные задачи, такие как обучение с подкреплением или обработка временных рядов? И самое главное — сможет ли эта математическая магия объяснить саму суть сознания, или же это всего лишь ещё одна красивая иллюзия, требующая жертв — и GPU?

---

Оригинал статьи: https://arxiv.org/pdf/2601.10482.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/