Искусственный интеллект
Оптимизация SciML: Путь к Быстрому Обучению Научных Моделей
Автор: Денис Аветисян
В этой статье представлен всесторонний обзор методов оптимизации, применяемых в научной машинном обучении (SciML), с акцентом на преодоление проблем жесткости и масштабируемости.
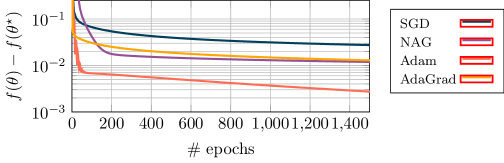
Рассмотрены стратегии предварительной обработки данных, параметров и функциональных пространств для повышения эффективности обучения SciML-моделей.
Оптимизация является ключевым компонентом как современного машинного обучения, так и научной машинной обработки (SciML), однако структура соответствующих задач существенно различается. В работе ‘Introduction to optimization methods for training SciML models’ представлен обзор методов оптимизации, применяемых в SciML, с акцентом на сложности, связанные с жесткостью и масштабируемостью, а также стратегии предобуславливания в пространствах данных, параметров и функций для повышения эффективности обучения. Ключевым отличием SciML является влияние спектральных свойств физических моделей на процесс оптимизации, что требует адаптации стандартных стохастических методов или использования детерминированных подходов, учитывающих кривизну. Какие новые алгоритмы и техники предобуславливания позволят преодолеть ограничения существующих методов и расширить возможности SciML?
Вызовы оптимизации в многомерных пространствах
Многие задачи в науке и технике требуют оптимизации функций, описываемых частными дифференциальными уравнениями (ЧДУ), часто в многомерных пространствах. Это особенно актуально в таких областях, как аэродинамика, моделирование потоков жидкости, теплопередача и электромагнетизм, где параметры системы могут быть представлены в виде векторов высокой размерности. Например, при проектировании крыла самолета необходимо оптимизировать его форму для достижения максимальной подъемной силы и минимального сопротивления, что требует решения ЧДУ, описывающих течение воздуха вокруг крыла, с учетом множества геометрических параметров. Сложность заключается в том, что с увеличением числа параметров, определяющих функцию, растет и сложность поиска оптимального решения, поскольку пространство поиска становится чрезвычайно большим и труднопроходимым. \nabla f(x) = 0 — поиск решения этой системы уравнений в многомерном пространстве часто становится вычислительно непосильным.
Традиционные методы оптимизации сталкиваются с серьезными трудностями при решении задач в многомерных пространствах, что обусловлено так называемым «проклятием размерности». Суть проблемы заключается в том, что с увеличением числа переменных объем пространства поиска решений экспоненциально возрастает, требуя при этом экспоненциально больше вычислительных ресурсов для его эффективного исследования. В сочетании со сложностью вычисления решений, определяемых частными дифференциальными уравнениями (ПДУ), это приводит к значительному увеличению вычислительных затрат и снижению эффективности традиционных алгоритмов. Решение ПДУ, особенно в высоких размерностях, может потребовать огромного количества операций, что делает стандартные методы оптимизации практически неприменимыми для многих реальных задач, включая проектирование материалов, моделирование климата и финансовое моделирование.
Физически информированные нейронные сети: новый подход
Нейронные сети, обученные с учетом физических законов (PINN), представляют собой новый подход к решению задач, в котором дифференциальные уравнения в частных производных (ДУЧП), описывающие физические процессы, непосредственно включаются в функцию потерь нейронной сети. Вместо традиционного обучения на больших объемах размеченных данных, PINN используют ДУЧП как регуляризатор, гарантирующий, что полученное решение удовлетворяет фундаментальным физическим принципам. Это достигается путем добавления к функции потерь члена, который измеряет невыполнение ДУЧП сетью. Таким образом, оптимизация функции потерь одновременно минимизирует расхождение между предсказаниями сети и доступными данными, а также обеспечивает соответствие решения физическим законам, определяемым ДУЧП вида \frac{\partial u}{\partial t} = \nabla \cdot (-k \nabla u) .
Особенностью сетей, обусловленных физикой (PINN), является способность к обучению решений, удовлетворяющих как имеющимся данным, так и фундаментальным физическим законам, описываемым дифференциальными уравнениями в частных производных (ДУЧП). Это достигается за счет интеграции ДУЧП непосредственно в функцию потерь нейронной сети. В результате, PINN могут эффективно аппроксимировать решения даже при ограниченном объеме размеченных данных, поскольку физические ограничения служат дополнительным источником информации и регуляризацией, уменьшая зависимость от больших обучающих выборок. Это особенно важно для задач, где получение большого количества размеченных данных является дорогостоящим или невозможным, а также для задач обратного моделирования, где необходимо найти параметры системы по наблюдаемым данным.
Ключевым элементом в архитектуре Physics-Informed Neural Networks (PINN) является правильно подобранная функция потерь (LossFunction), обеспечивающая баланс между соответствием данным и удовлетворением физическим законам, описываемым дифференциальными уравнениями в частных производных (ДУЧП). Функция потерь обычно состоит из нескольких компонентов: потери данных, измеряющие расхождение между предсказаниями сети и имеющимися данными, и потери, связанные с ДУЧП, которые оценивают, насколько хорошо решение сети удовлетворяет этим уравнениям. Веса, присваиваемые каждому компоненту, определяют относительную важность соответствия данным и физической корректности. Оптимизация функции потерь осуществляется с использованием алгоритмов градиентного спуска, что позволяет сети находить решения, одновременно соответствующие экспериментальным данным и удовлетворяющие фундаментальным физическим принципам. Выбор и настройка весов в функции потерь критически важны для обеспечения стабильности обучения и получения точных, физически обоснованных результатов.
Повышение эффективности PINN с помощью продвинутой оптимизации
В задачах обучения физически информированных нейронных сетей (PINN) широко используются методы первого порядка, такие как стохастический градиентный спуск (SGD), Momentum и Adam. Эти алгоритмы, несмотря на свою популярность и простоту реализации, часто демонстрируют медленную сходимость, особенно при решении сложных задач или работе с большими объемами данных. Причинами низкой скорости сходимости являются, в частности, неэффективная эксплуатация информации о кривизне оптимизируемого пространства и возможность застревания в локальных минимумах. Выбор подходящей скорости обучения и использование техник регуляризации могут частично смягчить проблему, однако, для достижения более высокой производительности часто требуется переход к методам второго порядка или использование техник предварительной обработки (preconditioning).
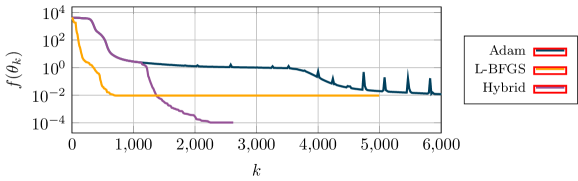
Методы второго порядка, такие как QuasiNewtonMethod, позволяют ускорить сходимость при обучении PINN за счет использования информации о кривизне целевой функции. В отличие от методов первого порядка, использующих только градиент, методы второго порядка аппроксимируют матрицу Гессе \nabla^2 f(x) , что позволяет более эффективно определять направление поиска минимума. CurvatureAwareOptimization — это подход, который адаптирует шаги оптимизации на основе анализа кривизны, позволяя избежать колебаний и ускорить сходимость, особенно в задачах с плохо обусловленными функциями потерь. В результате, методы второго порядка демонстрируют более высокую скорость сходимости по сравнению со стандартными алгоритмами, такими как Stochastic Gradient Descent (SGD), Momentum и Adam, особенно в задачах с большим количеством параметров или сложной геометрией.
Для дальнейшей оптимизации обучения PINN применяются методы предварительной подготовки (прекондиционирования), направленные на изменение геометрии пространства оптимизации. DataSpacePreconditioning масштабирует и сдвигает данные, используемые для расчета потерь, с целью улучшения обусловленности задачи. ParameterSpacePreconditioning модифицирует пространство параметров модели, упрощая ландшафт оптимизации и ускоряя сходимость. FunctionSpacePreconditioning работает с функциональным пространством решения, преобразуя исходную задачу в эквивалентную, но более удобную для оптимизации, что позволяет сократить количество итераций, необходимых для достижения заданной точности.
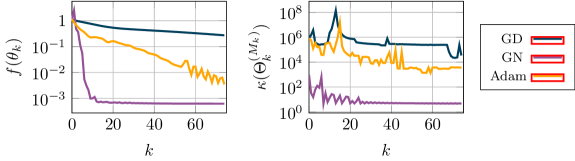
Масштабирование PINN для многомерных задач
Разложение области (Domain Decomposition) представляет собой эффективный подход к решению сложных задач, особенно в контексте физически информированных нейронных сетей (PINN). Суть метода заключается в разделении исходной задачи на множество более мелких, независимых подзадач, каждая из которых решается параллельно. Такой подход не только существенно снижает требования к вычислительной памяти, поскольку каждая подзадача требует меньше ресурсов, но и позволяет значительно ускорить процесс решения благодаря возможности параллельных вычислений. Каждая подзадача решается на своей части общей области, а затем результаты объединяются для получения решения исходной задачи. Это особенно важно при моделировании сложных систем с высокой размерностью, где традиционные численные методы могут сталкиваться со значительными трудностями в плане вычислительной эффективности и потребления памяти.
Многоуровневый метод представляет собой инновационный подход к оптимизации, использующий иерархию представлений для повышения эффективности решения сложных задач, особенно тех, которые характеризуются многомасштабностью. Суть метода заключается в построении последовательности приближений, начиная с грубого представления и постепенно уточняя детали на каждом уровне. Такой подход позволяет значительно ускорить сходимость алгоритма, поскольку на начальных этапах оптимизация происходит в пространстве низкого разрешения, что снижает вычислительную нагрузку. По мере уточнения представления, алгоритм фокусируется на более мелких деталях, обеспечивая высокую точность решения. \frac{d^2u}{dx^2} Этот метод особенно эффективен при решении задач, где присутствуют резкие градиенты или сложные геометрические формы, поскольку он позволяет адаптировать разрешение к локальным особенностям задачи, избегая избыточных вычислений в областях с небольшими изменениями.
Разработанные методы позволили нейронным сетям, обученным с помощью физически информированного подхода (PINN), решать задачи, ранее считавшиеся непосильными. В областях, таких как гидродинамика, теплопередача и строительная механика, стало возможным моделирование сложных процессов в многомерных пространствах. Улучшенная масштабируемость, достигнутая благодаря этим технологиям, открывает перспективы для точного анализа и прогнозирования поведения систем, характеризующихся высокой сложностью геометрии и физических явлений. Например, моделирование турбулентного потока или распространения тепла в сложных конструкциях теперь может быть выполнено с приемлемой вычислительной эффективностью, что ранее представляло значительную проблему для численных методов.
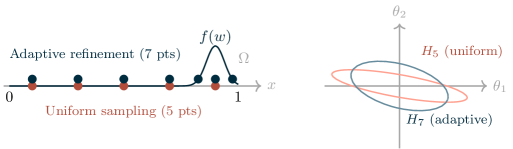
Исследование методов оптимизации в SciML демонстрирует, что каждая архитектура проходит свой жизненный цикл, сталкиваясь с проблемами жёсткости и масштабируемости. Применение стратегий предобуславливания в пространстве данных, параметров и функций — это попытка замедлить неизбежное старение, но даже самые передовые улучшения со временем устаревают. Как отмечал Вернер Гейзенберг: «Самая важная цель науки — не сбор знаний, а развитие способности мыслить». Иными словами, понимание принципов оптимизации и адаптация к новым вызовам — это залог долговечности любой системы машинного обучения, а не просто накопление алгоритмов.
Что впереди?
Представленный обзор методов оптимизации для обучения SciML-моделей лишь обозначил границы текущего понимания. Каждая неспособность алгоритма сойтись — это сигнал времени, напоминание о том, что пространство параметров, в котором мы ищем решения, бесконечно сложнее, чем наши представления о нем. Жесткость систем, масштабность задач — эти препятствия не столько решаются, сколько временно обходят стороной, оставляя фундаментальные вопросы нетронутыми.
Вероятно, будущее SciML лежит не в создании принципиально новых оптимизаторов, а в более глубоком осмыслении природы самих моделей. Рефакторинг — это диалог с прошлым, попытка понять, какие упрощения и предположения были сделаны, и как они влияют на способность модели к обучению. Необходимо переосмыслить роль априорных знаний, перейти от простого включения физических законов к формированию самосогласующихся моделей, способных адаптироваться к неполноте данных.
И все же, каждый новый метод, каждая уловка, позволяющая немного ускорить обучение, — это не победа над временем, а лишь отсрочка неизбежного. Все системы стареют — вопрос лишь в том, делают ли они это достойно. Задача состоит не в том, чтобы создать идеальный алгоритм, а в том, чтобы создать инструменты, позволяющие извлекать максимум информации из ограниченных ресурсов, пока время не сделало свое дело.
Оригинал статьи: https://arxiv.org/pdf/2601.10222.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Статья также опубликована на личном сайте автора.