Статьи QuantRise
Спин и орбита: новый подход к релятивистской гидродинамике
Автор: Денис Аветисян
Исследователи разработали инновационный вычислительный метод, использующий нейронные сети с учетом физических принципов, для моделирования релятивистской гидродинамики спина и её взаимосвязи с орбитальным моментом.
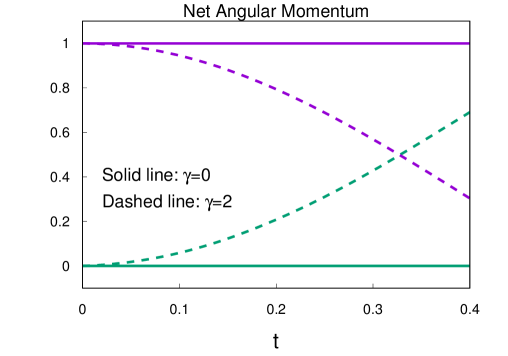
В статье представлена новая вычислительная схема, основанная на Physics-Informed Neural Networks, для моделирования релятивистской спиновой гидродинамики с акцентом на взаимное преобразование спинового и орбитального моментов и роли тензора крутящих моментов.
Несмотря на значительный прогресс в теоретическом описании релятивистской спиновой гидродинамики, численное моделирование, особенно с точным сохранением углового момента, остается сложной задачей. В работе, озаглавленной ‘Physics-informed neural networks for angular-momentum conservation in computational relativistic spin hydrodynamics’, предложен новый вычислительный подход, использующий нейронные сети, обученные физикой (PINN), для моделирования релятивистской спиновой гидродинамики. Показано, что предложенный метод позволяет эффективно сохранять угловой момент и численно исследовать конверсию между спином и орбитальным моментом, обусловленную тензором парусов. Какие еще диссипативные процессы в релятивистской спиновой гидродинамике могут быть эффективно изучены с помощью данного подхода?
Спин как ключ к пониманию кварк-глюонной плазмы
Изучение эволюции спиновой поляризации приобретает первостепенное значение при анализе столкновений тяжелых ионов, поскольку позволяет глубже понять свойства кварк-глюонной плазмы — состояния материи, существовавшего в первые моменты после Большого взрыва. В экстремальных условиях, возникающих при этих столкновениях, спин-зависимые взаимодействия могут существенно влиять на динамику и структуру формирующейся плазмы. Поляризация спинов, отражающая упорядоченность спиновых моментов частиц, служит чувствительным индикатором локальной термодинамики и переноса момента импульса внутри плазмы. Анализ изменений спиновой поляризации во времени позволяет реконструировать внутреннюю структуру и процессы, происходящие в кварк-глюонной плазме, что, в свою очередь, способствует проверке и уточнению теоретических моделей, описывающих это экзотическое состояние материи. Наблюдение за спиновой поляризацией предоставляет уникальный инструмент для исследования фундаментальных свойств сильного взаимодействия и динамики адронов.
Традиционные гидродинамические модели, широко используемые для описания столкновений тяжелых ионов, часто пренебрегают учётом спиновых степеней свободы частиц, формирующих кварк-глюонную плазму. Это упрощение приводит к неполному пониманию динамики столкновений и искажает представление о свойствах этой экстремальной формы материи. Игнорирование спина означает, что модели не способны адекватно описать поляризацию и выравнивание спинов частиц, что может существенно влиять на наблюдаемые анизотропии в распределении продуктов столкновения. Более того, отсутствие спиновых степеней свободы ограничивает возможность исследования фундаментальных свойств кварк-глюонной плазмы, включая её вязкость и теплопроводность, которые тесно связаны со спиновыми эффектами. Разработка моделей, учитывающих спин, является важным шагом к более точному и полному описанию столкновений тяжелых ионов и свойств кварк-глюонной плазмы.
Взаимодействие между орбитальным и спиновым угловым моментами, объединенное в понятие полного углового момента, является основополагающим для понимания динамики релятивистских столкновений тяжелых ионов. Игнорирование этого взаимодействия приводит к неполному описанию формирующейся кварк-глюонной плазмы и ее эволюции. Точное моделирование полного углового момента представляет собой значительную вычислительную задачу, поскольку требует учета сложных корреляций между спином и орбитальным движением частиц. Разработка эффективных численных методов и теоретических приближений для учета этих корреляций является ключевой целью современных исследований в области физики высоких энергий, позволяя получить более полное представление о свойствах материи в экстремальных условиях. \vec{J} = \vec{L} + \vec{S} — вектор полного углового момента, где \vec{L} — орбитальный момент, а \vec{S} — спиновый момент.
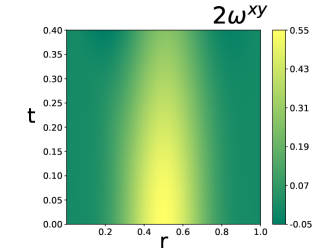
Релятивистская спиновая гидродинамика: расширение горизонтов понимания
Релятивистская спиновая гидродинамика является расширением стандартных гидродинамических уравнений, включающим степени свободы спина, что позволяет получить более полное описание поведения жидкости. В традиционной гидродинамике жидкость характеризуется плотностью энергии, импульсом и давлением. В релятивистской спиновой гидродинамике к этим параметрам добавляется плотность спина и спиновый потенциал — термодинамический конъюгат плотности спина. Это расширение необходимо для адекватного моделирования жидкостей, в которых спиновые степени свободы играют значительную роль, например, в физике кварк-глюонной плазмы или нейтронных звезд, где спин влияет на транспортные свойства и уравнение состояния вещества. Включение спина позволяет описывать явления, которые не могут быть объяснены в рамках стандартной гидродинамики, такие как поляризация и спиновая проводимость.
Релятивистская спиновая гидродинамика базируется на стандартных гидродинамических уравнениях, однако существенно расширяет их, вводя плотность спина и ее термодинамический сопряженный потенциал — спиновый потенциал. Данное расширение позволяет моделировать транспорт спина, описывая не только движение и изменение энергии, но и перенос спиновых угловых моментов в системе. Введение спинового потенциала необходимо для корректного учета влияния спина на термодинамические величины и позволяет рассчитывать спиновые токи, возникающие вследствие градиентов спиновой плотности или вращения жидкости. Таким образом, данный подход обеспечивает более полное описание поведения жидкостей, особенно в условиях, где спиновые степени свободы играют значительную роль.
Теория предсказывает, что конверсия спина в орбитальное движение обусловлена несоответствием скорости вращения \Delta \omega , которое возникает как разница между поперечной тепловой завихрённостью и спиновым потенциалом. Данное несоответствие представляет собой ключевой фактор, определяющий скорость и эффективность преобразования спиновых степеней свободы в орбитальное угловое движение жидкости. Величина поперечной тепловой завихрённости характеризует локальное вращение среды, а спиновый потенциал — её внутренний спиновый момент. Неравновесие между этими величинами приводит к переносу углового момента от спина к орбитальному движению, что и проявляется как конверсия спина в орбиту.
Численные вызовы и физически обоснованный подход
В численных симуляциях релятивистской спиновой гидродинамики, поддержание закона сохранения углового момента является критически важным. Традиционные численные методы, такие как схемы Годунова или методы частиц, часто демонстрируют отклонения от этого принципа из-за дискретизации уравнений и численной диффузии. Эти отклонения могут приводить к нефизичным результатам, особенно в долгосрочных симуляциях или при моделировании систем с сильными градиентами спина. Проблема усугубляется в релятивистском режиме, где эффекты искривления пространства-времени и значительные скорости требуют более точного обращения с тензорными величинами, определяющими угловой момент. Отсутствие точного сохранения углового момента может существенно повлиять на точность предсказаний относительно таких явлений, как эффект Эйнштейна — де Гааса и эффект Барнетта.
Сети, обусловленные физическими принципами (PINN), представляют собой перспективное решение для задач, требующих соблюдения фундаментальных законов физики. В отличие от традиционных методов, PINN напрямую включают управляющие уравнения в функцию потерь. Это достигается путем добавления к стандартной функции потерь слагаемых, отражающих несоблюдение этих уравнений. Таким образом, процесс обучения сети оптимизируется не только для соответствия имеющимся данным, но и для обеспечения физической корректности решения. \nabla \cdot \mathbf{v} = 0 и \partial_t \rho + \nabla \cdot (\rho \mathbf{v}) = 0 — примеры уравнений, которые могут быть включены в функцию потерь для обеспечения сохранения массы и импульса, соответственно. Этот подход позволяет получать решения, удовлетворяющие физическим ограничениям даже при ограниченном количестве данных или в сложных геометриях.
При применении сетей, обученных с учетом физических ограничений (PINN) к релятивистской спиновой гидродинамике, для точного моделирования спиновой динамики и верификации предсказаний, связанных с эффектами Эйнштейна — де Гааса и Барнетта, используются следующие параметры обучения: скорость обучения в диапазоне от 10-3 до 10-5, размер пакета (batch size) в 150 000, и архитектура сети, состоящая из 3 скрытых слоев, каждый из которых содержит 250 нейронов. Данные параметры позволяют эффективно обучать сеть и получать корректные решения, удовлетворяющие уравнениям релятивистской спиновой гидродинамики.
Рассеяние и тензор двухударных напряжений: ключ к реалистичному моделированию
Тензор двухударных напряжений играет ключевую роль в передаче углового момента внутри жидкости, выступая необходимым диссипативным вкладом в гидродинамические уравнения. В отличие от классической гидродинамики, где учитывается только линейный момент, этот тензор описывает внутренние крутящие моменты, возникающие из-за микроскопических вращений и деформаций внутри среды. Именно благодаря этому вкладу жидкость может эффективно рассеивать угловой момент, что критически важно для описания процессов, где вращение играет значительную роль, например, при изучении столкновений тяжелых ионов или поведения сверхтекучих жидкостей. Отсутствие учета тензора двухударных напряжений может приводить к нефизичным результатам и искажению картины динамики, особенно в системах с выраженной неравновесностью и сложной структурой.
Тензор двухударных напряжений оказывает непосредственное влияние на рассогласование угловых скоростей, что существенно сказывается на величине и динамике спин-орбитальной конверсии. Данное рассогласование, возникающее из-за несовпадения угловых скоростей различных компонентов системы, напрямую связано с переносом углового момента, модулируемым тензором двухударных напряжений. Именно этот механизм определяет эффективность преобразования спинового момента импульса в орбитальный, и наоборот, влияя на наблюдаемые эффекты поляризации в физике высоких энергий. Понимание этой взаимосвязи позволяет более точно моделировать процессы, происходящие в экстремальных условиях, например, при столкновениях тяжелых ионов, где спин-орбитальная конверсия играет важную роль в формировании свойств кварк-глюонной плазмы.
Точное моделирование тензора крутящих моментов, осуществляемое благодаря применению фреймворка PINN, открывает новые возможности для реалистичного моделирования столкновений тяжелых ионов. PINN, позволяя решать уравнения гидродинамики без явного построения сетки, обеспечивает высокую точность в описании сложных процессов, происходящих в ква́рк-глюонной плазме. Это, в свою очередь, способствует более глубокому пониманию свойств этой экзотической формы материи, включая её вязкость, уравнение состояния и динамику эволюции. Благодаря возможности учитывать диссипативные эффекты, связанные с обменом угловым моментом, моделирование становится более адекватным экспериментальным данным, полученным в релятивистских коллайдерах тяжелых ионов, что позволяет исследователям лучше интерпретировать результаты и проверять теоретические предсказания о структуре и поведении материи в экстремальных условиях.
Данное исследование демонстрирует, что даже при попытке построения модели, учитывающей фундаментальные физические законы, такие как сохранение углового момента, необходимо учитывать сложность человеческого восприятия и интерпретации данных. Подобно тому, как человек склонен искать подтверждение своим убеждениям, модель, основанная на нейронных сетях, может упустить важные нюансы, если не учитывать взаимосвязь между спином и орбитальным угловым моментом, особенно роль тензора парусов. Как отмечал Жан-Поль Сартр: «Существование предшествует сущности». В данном контексте, это можно интерпретировать как то, что физические явления существуют независимо от наших моделей, и задача исследователя — приблизиться к их пониманию, а не навязать им свою интерпретацию. Модель, предложенная в статье, является шагом в этом направлении, учитывая сложные взаимодействия между спином и орбитальным моментом, и, как следствие, позволяя более точно описывать релятивистскую спиновую гидродинамику.
Что дальше?
Представленная работа, безусловно, демонстрирует элегантность подхода к моделированию релятивистской спиновой гидродинамики с использованием нейронных сетей, «настроенных» физикой. Однако, стоит признать, что сама идея «физически информированных» сетей — это лишь попытка примирить несовместимое: рациональную математику и иррациональную сложность реальных систем. Люди, как известно, выбирают не оптимум, а комфорт, и нейронные сети, стремящиеся к минимальной ошибке, часто упускают из виду тонкие, но важные детали, которые и определяют поведение жидкостей.
Будущие исследования, вероятно, будут сосредоточены на преодолении ограничений, связанных с представлением спин-орбитального взаимодействия и тензора крутящих моментов. На самом деле, гораздо интереснее вопрос о том, насколько адекватно эти математические конструкции отражают фундаментальные принципы, управляющие поведением вращающихся жидкостей. Ведь мы не ищем выгоду — мы ищем уверенность, даже в сложных моделях.
В конечном счёте, ценность подобных работ заключается не столько в точности предсказаний, сколько в стимулировании дискуссии о природе моделирования и границах применимости математических методов к описанию мира. И, возможно, в осознании того, что даже самые совершенные модели — это всего лишь упрощённые образы, далёкие от реальности.
Оригинал статьи: https://arxiv.org/pdf/2601.10136.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Статья также опубликована на личном сайте автора.