Статьи QuantRise
Точность симуляций: Как правильно оценить истинные значения в причинно-следственных исследованиях
Автор: Денис Аветисян
В новой работе исследователи предлагают методы повышения точности расчетов при проверке причинно-следственных связей в смоделированных данных.
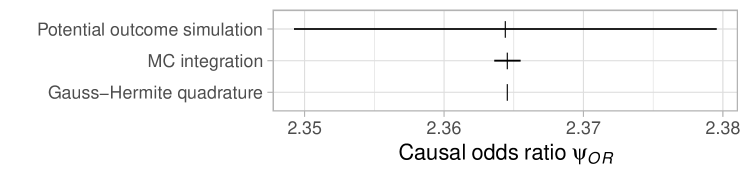
Оценка точности интегральных методов, включая квадратуры Гаусса и Монте-Карло, при расчете целевых параметров в симуляционных исследованиях причинно-следственных связей.
Во многих исследованиях причинно-следственных связей, несмотря на наличие симуляций, точное вычисление истинных значений оцениваемых параметров остается сложной задачей. В статье ‘Revealing the Truth: Calculating True Values in Causal Inference Simulation Studies via Gaussian Quadrature’ рассматривается применение квадратур Гаусса для эффективного и точного вычисления целевых параметров в симуляционных исследованиях, в частности, средних причинных эффектов. Показано, что квадратурные методы превосходят методы Монте-Карло по скорости и точности, предлагая надежный инструмент для оценки свойств статистических методов. Не откроет ли это подход новые возможности для повышения достоверности и эффективности симуляционных исследований в области причинно-следственного анализа?
Символы и Предсказания: Основы Оценки
Статистический вывод напрямую зависит от четко определенных величин, известных как estimands — параметров, которые стремятся оценить. Однако, вычисление этих estimands зачастую представляет собой сложную задачу, требующую значительных вычислительных ресурсов. Сложность возникает из-за необходимости моделирования сложных взаимосвязей в данных, а также из-за стремления к высокой точности. Особенно остро эта проблема проявляется при работе с большими объемами данных или при анализе моделей, содержащих множество параметров. Несмотря на теоретическую ясность определения estimands, их практическая оценка может потребовать значительного времени и вычислительной мощности, что ограничивает возможности проведения всестороннего анализа и получения надежных результатов. E[Y] — пример estimand, который может быть сложен в вычислении, в зависимости от распределения Y и сложности модели.
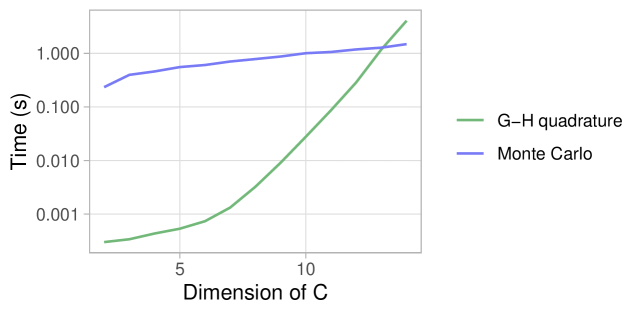
Традиционные методы Монте-Карло, несмотря на свою гибкость и широкую применимость, зачастую демонстрируют медленную сходимость, особенно при работе со сложными моделями. Для достижения сравнимой точности в таких случаях может потребоваться анализ порядка 10^9 выборок, что представляет собой значительную вычислительную нагрузку. Эта проблема существенно ограничивает возможности проведения детальных исследований и анализа, поскольку время вычислений и требуемые ресурсы становятся непомерно высокими. В результате, исследователи могут быть вынуждены идти на компромиссы в точности, что, в свою очередь, влияет на надежность полученных результатов и достоверность выводов.
Вычислительная сложность, связанная с получением точных оценок, существенно ограничивает возможности проведения многих аналитических исследований. Потребность в огромном количестве симуляций — порядка 10^9 и более — для достижения приемлемой точности, делает невозможным анализ сложных моделей в разумные сроки и с доступными ресурсами. Это особенно актуально в областях, требующих высокой степени достоверности, таких как клинические испытания или финансовое моделирование. Вследствие этого, исследователи часто вынуждены идти на компромисс между точностью и скоростью, что может приводить к неверным выводам и упущенным возможностям. Необходимость оптимизации вычислительных методов и разработки более эффективных алгоритмов становится критически важной для продвижения научных исследований и принятия обоснованных решений.
Квадратуры: Альтернативный Путь Вычислений
Квадратурные методы представляют собой детерминированный подход к численному интегрированию, в отличие от стохастических методов, таких как симуляция Монте-Карло. В то время как методы Монте-Карло полагаются на случайную выборку для аппроксимации интеграла, квадратурные методы используют предопределенные точки (узлы) и соответствующие веса для вычисления конечной суммы, представляющей интеграл. Это обеспечивает предсказуемую точность и сходимость, что может быть критически важно в задачах, где требуется высокая надежность результатов или где случайные ошибки недопустимы. В отличие от Монте-Карло, точность квадратурных методов можно улучшить за счет увеличения числа узлов, хотя существует предел эффективности, обусловленный сложностью интегрируемой функции и свойствами выбранной квадратурной формулы.
Квадратура Гаусса обеспечивает высокую точность численного интегрирования за счет использования специально подобранных узлов (точек) и весов. В отличие от методов, использующих равномерное разбиение интервала интегрирования, узлы в квадратуре Гаусса располагаются в определенных точках, являющихся корнями ортогональных полиномов. Соответствующие веса определяются аналитически и зависят от выбранного полинома. Такой подход позволяет аппроксимировать интеграл с использованием меньшего числа оценок функции, чем традиционные методы, особенно для функций с гладким поведением. Точность метода зависит от степени полинома, используемого для определения узлов и весов, и, как правило, быстро сходится к истинному значению интеграла. Формула квадратуры Гаусса имеет вид: \in t_a^b f(x) dx \approx \sum_{i=1}^n w_i f(x_i) , где x_i — узлы, w_i — веса, а n — количество узлов.
Квадратура Гаусса-Эрмита представляет собой специализированный метод численного интегрирования, оптимизированный для функций, содержащих нормально распределенные переменные. В отличие от общей квадратуры Гаусса, использующей полиномы Лежандра и весовые коэффициенты, соответствующие корням этих полиномов, квадратура Гаусса-Эрмита использует полиномы Эрмита в качестве базисных функций и соответствующие эрмитовские гауссовы веса и узлы. Это позволяет достичь высокой точности при интегрировании функций вида \in t_{-\in fty}^{\in fty} f(x) e^{-x^2} dx с меньшим количеством вычислений функции, чем при использовании стандартных методов, особенно в задачах, связанных с вероятностью и статистикой. Преимущество обусловлено тем, что веса и узлы выбираются таким образом, чтобы учитывать гауссову форму подынтегральной функции, что повышает эффективность вычислений и снижает погрешность.
Математические Основы Квадратурных Методов
Полиномы Лежандра являются основой для определения оптимальных узлов и весов, используемых в квадратуре Гаусса. Узлы квадратуры Гаусса — это корни полинома Лежандра P_n(x) порядка n, а веса вычисляются по формуле, связанной с производной полинома Лежандра. Использование этих узлов и весов позволяет добиться максимальной точности при численном интегрировании, поскольку квадратура Гаусса порядка n точно интегрирует все полиномы степени не выше 2n-1. По сути, полиномы Лежандра обеспечивают ортогональную систему функций, которая минимизирует погрешность численного интегрирования, определяя наиболее эффективное расположение точек для аппроксимации интеграла.
Ортогональные полиномы обеспечивают систематический подход к приближенному вычислению определенных интегралов с высокой точностью благодаря их свойствам ортогональности и возможности построения базиса для пространства функций. В основе метода Гаусса заключается выбор точек (узлов) и весов, которые минимизируют ошибку приближения. Для интегралов вида \in t_a^b f(x) dx выбор узлов и весов, основанный на ортогональных полиномах, позволяет получить квадратурную формулу, которая точно вычисляет интеграл от полиномов степени не выше степени полинома, используемого при построении ортогональной системы. Это приводит к экспоненциальному уменьшению ошибки при увеличении числа узлов, что обеспечивает высокую точность приближения даже для сложных интегралов.
Переход к квадратуре Гаусса-Эрмита требует учета специфических свойств нормального распределения N(0, 1). В отличие от квадратуры Гаусса, использующей полиномы Лежандра и весовые коэффициенты, соответствующие корням этих полиномов, квадратура Гаусса-Эрмита использует полиномы Эрмита в качестве базисных функций. Интегрирование по нормальному распределению включает в себя умножение подынтегральной функции на e^{-x^2}, что влияет на выбор весовых коэффициентов и узлов интегрирования. Корни полиномов Эрмита, определяющие узлы квадратуры, и весовые коэффициенты рассчитываются с учетом интеграла от e^{-x^2} и свойств ортогональности полиномов Эрмита, обеспечивая высокую точность аппроксимации интегралов, содержащих этот фактор.
Влияние на Анализ Выживаемости и Причинно-Следственный Анализ
Точное вычисление ограниченного среднего времени до события RMST играет ключевую роль в оценке эффективности лечения в анализе выживаемости. В отличие от традиционных показателей, таких как медиана выживаемости, RMST позволяет более полно оценить влияние лечения на продолжительность жизни пациентов, особенно в случаях, когда кривые выживаемости пересекаются или когда эффект лечения проявляется не сразу. По сути, RMST представляет собой среднее время до события для всех пациентов, ограничивающее рассмотрение определенным периодом времени, что делает его более чувствительным к различиям в кривых выживаемости, возникающим на разных временных интервалах. Использование точных методов оценки RMST позволяет исследователям и клиницистам более надежно интерпретировать результаты клинических испытаний и принимать обоснованные решения о лечении.
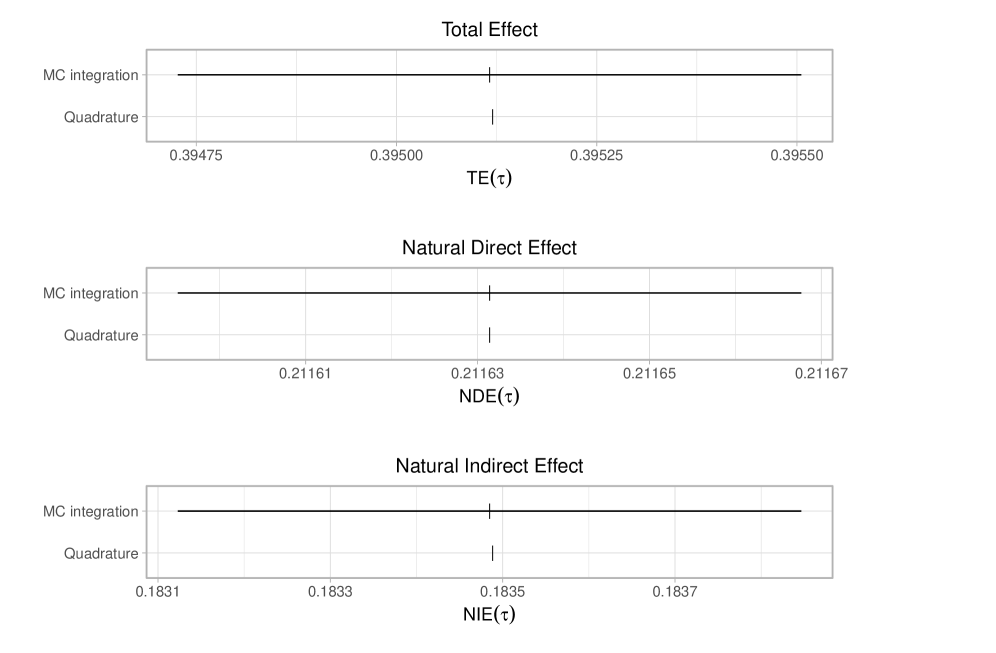
Методы квадратур позволяют с высокой точностью вычислять естественные прямые и непрямые эффекты, углубляя понимание причинно-следственных механизмов. В отличие от традиционных подходов, требующих больших вычислительных затрат, квадратурные техники обеспечивают надежные оценки этих эффектов, раскрывая, как конкретное вмешательство влияет на исход через различные пути. Это особенно важно в исследованиях, где необходимо отделить истинный эффект от искажений, вызванных смешивающими факторами. Точный расчет естественных прямых и непрямых эффектов позволяет исследователям более четко определить, какие механизмы лежат в основе наблюдаемых результатов, что способствует разработке более эффективных стратегий вмешательства и персонализированной медицины. Полученные результаты способствуют более детальному анализу сложных взаимосвязей и позволяют выявить скрытые факторы, влияющие на наблюдаемые явления.
Оценка общего эффекта воздействия лечения, представляющего собой совокупное влияние на пациента, теперь может быть выполнена с высокой точностью благодаря новым методам. Исследования показали, что предложенные вычислительные подходы позволяют надежно определить этот эффект всего за 0.073 секунды. Это значительно быстрее, чем традиционные методы, такие как Монте-Карло интеграция, требующие 0.44 секунды для достижения сопоставимой точности. Такое ускорение вычислений открывает возможности для анализа больших массивов данных и более эффективной оценки эффективности различных терапевтических стратегий, что особенно важно в клинических исследованиях и персонализированной медицине.
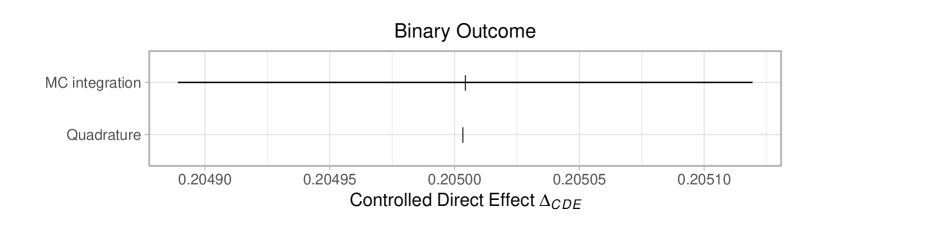
Надежная Оценка Через Моделирование
Исследования с использованием моделирования играют ключевую роль в оценке надежности статистических методов и оцениваемых параметров в разнообразных условиях. Вместо полагания исключительно на реальные данные, которые могут быть ограничены или не отражать весь спектр возможных ситуаций, моделирование позволяет исследователям создавать искусственные наборы данных, контролируя при этом все факторы, влияющие на результаты. Это особенно важно при оценке производительности новых статистических подходов или при изучении поведения параметров в сценариях, которые трудно или невозможно наблюдать в реальной практике. Такой подход дает возможность всесторонне проверить устойчивость и точность методов, выявить потенциальные проблемы и оптимизировать их для достижения наилучших результатов в различных условиях, обеспечивая уверенность в обоснованности выводов и надежности принимаемых решений.
Исследователи активно используют методы моделирования результатов и потенциальных результатов для создания реалистичных наборов данных, необходимых для оценки статистических методов и оцениваемых показателей. Данные подходы позволяют имитировать сложные взаимосвязи и вариабельность, характерные для реальных условий, что особенно важно при изучении сценариев, где сбор фактических данных затруднен или невозможен. Моделирование результатов фокусируется на генерации наблюдаемых данных, учитывая определенные параметры модели, в то время как моделирование потенциальных результатов позволяет оценить влияние различных вмешательств или факторов, рассматривая, какие результаты могли бы быть получены при иных обстоятельствах. Эти методы не только повышают надежность оценки, но и способствуют более глубокому пониманию лежащих в основе механизмов, обеспечивая возможность тестирования различных гипотез и оптимизации статистических процедур.
Сочетание квадратурных методов с техниками Монте-Карло интеграции представляет собой мощный и гибкий инструментарий для генерации данных, используемых в статистических исследованиях. Вместо прямого численного интегрирования, которое может быть вычислительно затратным, квадратурные методы аппроксимируют интеграл с помощью взвешенной суммы значений функции в определенных точках. Применение различных распределений вероятностей, таких как равномерное, экспоненциальное и гамма-распределение, в рамках Монте-Карло интеграции позволяет эффективно оценивать сложные интегралы, моделируя случайные величины и их взаимосвязи. Такой подход обеспечивает детерминированную точность в сочетании со значительным снижением вычислительных затрат, что особенно важно при анализе больших объемов данных и проведении симуляционных исследований для оценки надежности статистических методов и оценок.
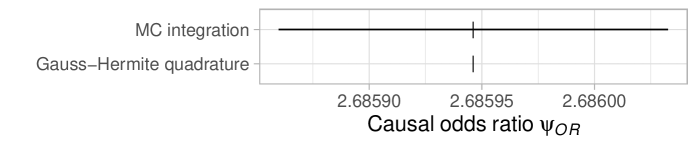
Исследование, посвященное оценке точности численных методов интеграции в контексте моделирования причинно-следственных связей, демонстрирует, что стремление к упрощению и скорости расчетов может приводить к скрытым погрешностям. Подобно тому, как при изучении небесных тел необходимо учитывать мельчайшие отклонения, так и в каузальном анализе, пренебрежение точностью интеграции может исказить истинные оценки эффектов. Галилей однажды сказал: «Вселенная — это книга, написанная на языке математики». В данном исследовании, математика интеграции становится инструментом для расшифровки этой книги, позволяя более точно оценивать сложные взаимосвязи и предсказывать последствия различных вмешательств. Применение квадратурных методов, как показано в работе, позволяет достичь большей скорости и точности, приближая нас к пониманию истинных значений оцениваемых параметров.
Что же дальше?
Представленная работа, исследуя точность численных методов в симуляционных исследованиях причинно-следственных связей, лишь обнажает более глубокую проблему. Стремление к идеальной симуляции — это иллюзия, попытка зафиксировать случайность в заранее заданных рамках. Каждый выбор алгоритма численного интегрирования — это пророчество о будущей ошибке, о той части реальности, которая неизбежно ускользнет от внимания. Чем точнее становится инструмент, тем сложнее признать границы его применимости.
Повышение скорости и точности вычислений, достигнутое с помощью квадратур, не решает фундаментальной дилеммы: симуляция всегда является упрощением. Разделение системы на компоненты, как в анализе опосредованных эффектов, не устраняет взаимозависимости, а лишь откладывает неизбежное проявление общей хрупкости. Всё связанное когда-нибудь рухнет синхронно, и даже самые изящные алгоритмы не смогут предотвратить этот коллапс.
Будущие исследования должны сосредоточиться не на усовершенствовании инструментов, а на признании их ограничений. Необходимо разрабатывать методы оценки погрешностей, которые учитывают не только статистические ошибки, но и систематические искажения, заложенные в самой модели симуляции. В конечном итоге, истинное понимание причинно-следственных связей требует не столько точных вычислений, сколько смирения перед сложностью мира.
Оригинал статьи: https://arxiv.org/pdf/2601.05128.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Статья также опубликована на личном сайте автора.