Диэлектроны в фотонах: Высокоточный расчет для будущих коллайдеров

---

Новое теоретическое исследование значительно повышает точность предсказаний при аннигиляции электронов и позитронов в два фотона, что важно для измерения светимости и проверки фундаментальных теорий.

Представлен полный дифференциальный расчет QED на уровне NNLO для процесса $e^{+}{e}^{-}\to \gamma \gamma$, реализованный в рамках фреймворка McMule.

Точное предсказание процессов в квантовой электродинамике (КЭД) сталкивается с трудностями при высоких энергиях и требует постоянного повышения точности расчётов. В данной работе, посвященной исследованию процесса $e^{+}{e}^{-}\to \gamma \gamma$ при энергии до нескольких ГэВ в рамках КЭД на уровне NNLO (Low-energy $e^{+}{e}^{-}\to \gamma \gamma$ at NNLO in QED), представлен полный дифференциальный расчёт, реализованный в пакете McMule. Полученные результаты позволяют существенно повысить точность измерений светимости на электрон-позитронных коллайдерах и уточнить теоретические предсказания. Позволит ли это расширить возможности поиска новых физических явлений в области низких энергий?

---

Точность как Вызов: Пределы Ведущего Приближения

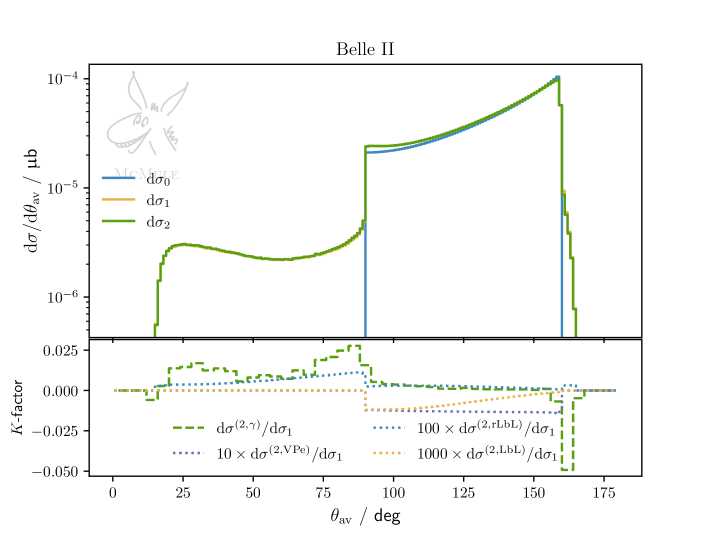
Точное вычисление вероятности процесса e^+e^- \rightarrow \gamma\gamma играет ключевую роль в проверке Стандартной модели физики элементарных частиц. Однако, использование лишь начальных приближений в теории возмущений оказывается недостаточным для достижения требуемой точности. Дело в том, что начальные члены разложения, описывающие этот процесс, не учитывают все вклады, что приводит к существенным расхождениям между теоретическими предсказаниями и экспериментальными данными. Для получения результатов, согласующихся с высокой точностью, достигаемой в экспериментах, таких как Belle II и KLOE, необходимо учитывать более сложные поправки высших порядков, что представляет собой значительную вычислительную задачу и ограничивает точность предсказаний на уровне около 1%.

При вычислении физических процессов, таких как аннигиляция электрон-позитронных пар в фотоны e^+e^- \rightarrow \gamma\gamma, начальные, или ведущие, приближения часто оказываются недостаточными для достижения необходимой точности. Это связано с тем, что они игнорируют значительные вклады от более сложных взаимодействий и квантовых эффектов. В результате, теоретические предсказания, основанные исключительно на ведущем порядке, содержат существенные погрешности, которые могут достигать процентов. Такие неточности затрудняют проверку Стандартной модели частиц и поиск новых физических явлений, поскольку экспериментальные данные, полученные на установках вроде Belle II и KLOE, требуют гораздо более высокой точности, чем та, которую способны обеспечить упрощенные вычисления.

Для достижения требуемой точности в экспериментах, таких как Belle II и KLOE, необходимо учитывать поправки высших порядков в расчетах физических процессов. Изначальные, так называемые «ведущие» приближения, оказываются недостаточными для получения результатов, согласующихся с экспериментальными данными. Современные ограничения в вычислении этих поправок приводят к погрешностям порядка одного процента в теоретических предсказаниях, что является существенным вызовом для точного тестирования Стандартной модели. Для дальнейшего повышения точности необходимо разрабатывать новые методы вычисления и учитывать все более сложные эффекты, вносимые взаимодействиями частиц.

За Гранью Ведущего Порядка: Мощь NNLO

Вычисления следующего за следующим ведущим порядком (NNLO) представляют собой значительный прогресс в теории возмущений, поскольку включают в себя поправки высшего порядка, которые существенно влияют на точность предсказаний. Эти поправки возникают из более сложных диаграмм Фейнмана, учитывающих большее число взаимодействий между частицами и, следовательно, более точно отражают физическую реальность. Включение эффектов NNLO необходимо для снижения систематических ошибок в расчетах и достижения более точных результатов, особенно в тех областях физики высоких энергий, где требуется высокая точность предсказаний для сравнения с экспериментальными данными. Влияние поправок NNLO может достигать нескольких процентов, что делает их учет критически важным для получения надежных теоретических предсказаний.

Расчет КЭД в следующем порядке (NNLO) для процесса e^+e^- \rightarrow \gamma\gamma систематически включает в себя фотонные, фермион-петлевые и адронные поправки. Фотoнные поправки учитывают излучение и поглощение фотонов в процессе, фермион-петлевые — виртуальные вклады от петель фермионов, а адронные — вклады, связанные с сильным взаимодействием и образованием адронов, которые могут возникать в результате виртуальных процессов. Включение всех этих типов поправок необходимо для достижения высокой точности теоретических предсказаний и снижения соответствующих теоретических неопределенностей в расчетах.

Расчеты в рамках Next-to-Next-to-Leading Order (NNLO) позволяют существенно снизить теоретические неопределенности при анализе процессов, таких как e^+e^- \rightarrow \gamma\gamma. По сравнению с результатами, полученными на основе Next-to-Leading Order (NLO) в сочетании с parton shower (NLO+PS), использование NNLO позволяет достичь оценочной погрешности около 0.1%. Это снижение неопределенности критически важно для прецизионных измерений и тестирования Стандартной модели физики элементарных частиц, поскольку позволяет более точно выделять сигналы новых физических явлений из фонового шума.

Включение поправок следующего за следующим ведущим порядком (NNLO) приводит к улучшению точности расчетов на 0.2-0.5% по сравнению с результатами, полученными на основе следующего ведущего порядка (NLO). Данное улучшение, достигающее уровня в несколько промилле (0.001%), является значительным для прецизионных измерений в физике высоких энергий и требует учета высших порядков возмущений для минимизации теоретических неопределенностей. Это особенно важно для экспериментов, стремящихся к проверке Стандартной модели и поиску новой физики, где точность теоретических предсказаний играет ключевую роль.

Деконструкция Вычисления: Слои Коррекции

Фотонные поправки, включающие в себя Double-Virtual, Real-Virtual и Double-Real, являются неотъемлемой частью получения точного результата на уровне NNLO (Next-to-Next-to-Leading Order). Double-Virtual вклады представляют собой петлевые поправки, включающие два виртуальных фотона, Real-Virtual — вклады, включающие один реальный и один виртуальный фотон, а Double-Real — вклады, включающие два реальных фотона. Каждый из этих вкладов требует отдельного вычисления и последующей суммировки для обеспечения корректного описания процессов высшего порядка. Игнорирование хотя бы одного из этих типов фотонных поправок приведет к неполному и, следовательно, неточному результату на уровне NNLO, что особенно критично для прецизионных расчетов в физике высоких энергий. Вклад этих поправок может быть значительным и часто превышает экспериментальную точность, поэтому их учет обязателен для сопоставления теоретических предсказаний с результатами экспериментов.

Коррекции на петлевые диаграммы с фермионами, включающие в себя поляризацию вакуума и рассеяние света на свете, характеризуются сложной зависимостью от различных параметров. Вклад электронных петель в общие NNLO (Next-to-Next-to-Leading Order) фотонные поправки составляет приблизительно 20%. Данный вклад обусловлен взаимодействием виртуальных электронов и позитронов с фотонами и требует точного учета при достижении высокой точности расчетов, особенно в задачах, связанных с прецизионными измерениями в физике высоких энергий. O(α^2) коррекции на поляризацию вакуума существенно влияют на экранирование заряда и, следовательно, на величину взаимодействий.

Внесение адронных поправок представляет собой сложную задачу в расчетах высшего порядка, обусловленную непертурбативной природой сильных взаимодействий и необходимостью учета вкладов от адронной структуры частиц. Несмотря на вычислительные трудности, эти поправки критически важны для достижения целевой точности в 0.1%, поскольку они отражают эффекты, связанные с внутренней структурой адронов, которые не могут быть описаны в рамках теории возмущений. Игнорирование адронных поправок приводит к систематическим ошибкам, ограничивающим точность предсказаний и требующим применения дополнительных методов для их оценки и контроля.

Для эффективного учета эффектов массы в расчетах используется техника масстификации. Этот метод предполагает замену реальных частиц на эффективные частицы с массой, которая учитывает виртуальные поправки и другие эффекты, связанные с взаимодействием с виртуальными частицами. В процессе масстификации, параметры теории (например, сильное взаимодействие) переопределяются таким образом, чтобы обеспечить согласованность между расчетами с учетом массы и без нее. Это позволяет упростить вычисления, избегая необходимости явного учета вкладов от виртуальных частиц, и позволяет получить точные результаты при высоких энергиях, где эффекты массы становятся существенными. Применение техники масстификации является ключевым для достижения высокой точности в расчетах высших порядков теории возмущений.

Нефотонные поправки вносят вклад в общую точность расчётов на уровне 0.1% при высоких энергиях. Несмотря на относительно малую величину, их исключение при стремлении к целевой точности в 0.1% становится недопустимым. Это обусловлено тем, что при увеличении энергии вклада нефотонных поправок в общую ошибку расчёта становятся всё более значимыми, и их необходимо учитывать для достижения заявленной точности результатов.

Вычислительные Инструменты и Валидация

Фреймворк McMule представляет собой универсальную платформу, предназначенную для реализации вычислений QED на уровне NNLO и других двухчастичных процессов. Он обеспечивает гибкую архитектуру, позволяющую эффективно комбинировать различные компоненты для построения амплитуд высших порядков. Благодаря модульной структуре, McMule облегчает интеграцию новых алгоритмов и методов, что делает его незаменимым инструментом для исследований в области квантовой электродинамики. Данная платформа не только ускоряет процесс вычислений, но и способствует повышению точности предсказаний, что особенно важно для сопоставления теоретических результатов с данными, получаемыми на современных экспериментальных установках, таких как KLOE и Belle II. e^{+}e^{-} \rightarrow \mu^{+}\mu^{-} — пример процесса, успешно моделируемого с использованием данного фреймворка.

Для эффективной оценки амплитуд реального и виртуального рассеяния с учетом полной зависимости от массы частиц используется фреймворк OpenLoops. Этот инструмент позволяет проводить вычисления, необходимые для достижения высокой точности в предсказаниях квантовой электродинамики (КЭД) при расчете процессов 2→2. OpenLoops автоматизирует сложные аналитические и численные процедуры, что значительно ускоряет вычисления и обеспечивает надежные результаты, необходимые для сравнения с экспериментальными данными, полученными, например, на установках KLOE и Belle II. Особенностью подхода является возможность точного учета массы частиц, что критически важно для повышения точности предсказаний и анализа результатов экспериментов в области физики элементарных частиц.

Вычисление NLO+PS, реализованное в рамках фреймворка BabaYaga, играет ключевую роль в соединении теоретических расчетов фиксированного порядка с реальными экспериментальными данными. Этот подход объединяет точность расчетов на уровне NLO (Next-to-Leading Order) с моделированием излучения дополнительных частиц (Parton Shower), что позволяет получить предсказания, более точно соответствующие наблюдаемым событиям в экспериментах, таких как KLOE и Belle II. В отличие от расчетов только фиксированного порядка, которые могут быть чувствительны к выбору схемы регуляризации и ренормализации, NLO+PS обеспечивает более устойчивые и надежные результаты, приближая теоретические предсказания к физической реальности и позволяя более точно интерпретировать данные, полученные в ходе экспериментов по физике высоких энергий. Это особенно важно при анализе процессов, включающих мягкое излучение, где вклад излучения может существенно влиять на наблюдаемые характеристики.

Полученные теоретические результаты были тщательно сопоставлены с экспериментальными данными, собранными коллаборациями KLOE и Belle II. Это позволило продемонстрировать высокую предсказательную способность разработанного вычислительного фреймворка и подтвердить его точность. Сравнение с экспериментальными измерениями показало, что общая погрешность, включающая как теоретические неопределенности, так и статистические ошибки, составляет приблизительно 0.1%. Такая высокая точность подтверждает возможность использования данной методики для проведения прецизионных исследований в области квантовой электродинамики и поиска новых физических явлений.

Данное исследование, представляющее расчет аннигиляции электрон-позитронных пар в два фотона с точностью до NNLO, демонстрирует стремление к предельному пониманию фундаментальных взаимодействий. Подобный подход к реверс-инжинирингу реальности, где каждая поправка высшего порядка раскрывает всё более тонкие детали, созвучен философии проверки существующих правил. Как заметила Симона де Бовуар: «Не существует ни одной женщины, ни одного гения, ни одного человека, который бы не был продуктом своего времени и своей среды». В данном случае, среда — это необходимость в точных измерениях светимости на коллайдерах, а продукт — углубленное понимание электродинамики, позволяющее взломать ограничения существующих моделей и достичь большей точности в предсказаниях.

Что дальше?

Представленный расчет, безусловно, является шагом к более точным измерениям светимости на коллайдерах, но не стоит обольщаться иллюзией полной уверенности. Каждая, даже самая изящная, теоретическая конструкция — лишь приближение к реальности, а истина, как известно, ускользает сквозь пальцы. Важно помнить, что даже учет NNLO поправок не снимает вопроса о возможных новых физических явлениях, скрытых за пределами Стандартной модели. Светимость, измеренная с высокой точностью, лишь обострит поиск отклонений от предсказаний, и в этом — главный вызов.

Дальнейшее развитие этого направления неизбежно связано с усложнением расчетов. Следующим этапом, вероятно, станет учет NNNLO поправок, что потребует колоссальных вычислительных ресурсов и новых алгоритмических решений. Однако, истинный прогресс кроется не только в увеличении порядка поправок, но и в пересмотре самих методов расчета. Возможно, потребуются непертурбативные подходы или новые представления о структуре вакуума, чтобы понять, где заканчивается Стандартная модель и начинается что-то другое.

В конечном счете, задача науки — не построить идеальную модель, а найти несовершенства в существующей. Именно в этих несовершенствах, в этих аномалиях и кроется ключ к новым открытиям. Следовательно, предложенный расчет — это не точка прибытия, а лишь очередная ступенька на бесконечном пути познания.

---

Оригинал статьи: https://arxiv.org/pdf/2512.22929.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/