Дробные уравнения: новый подход к точному решению

---

Исследование представляет усовершенствованный численный метод для эффективного и высокоточного решения дробных дифференциальных уравнений высших порядков.

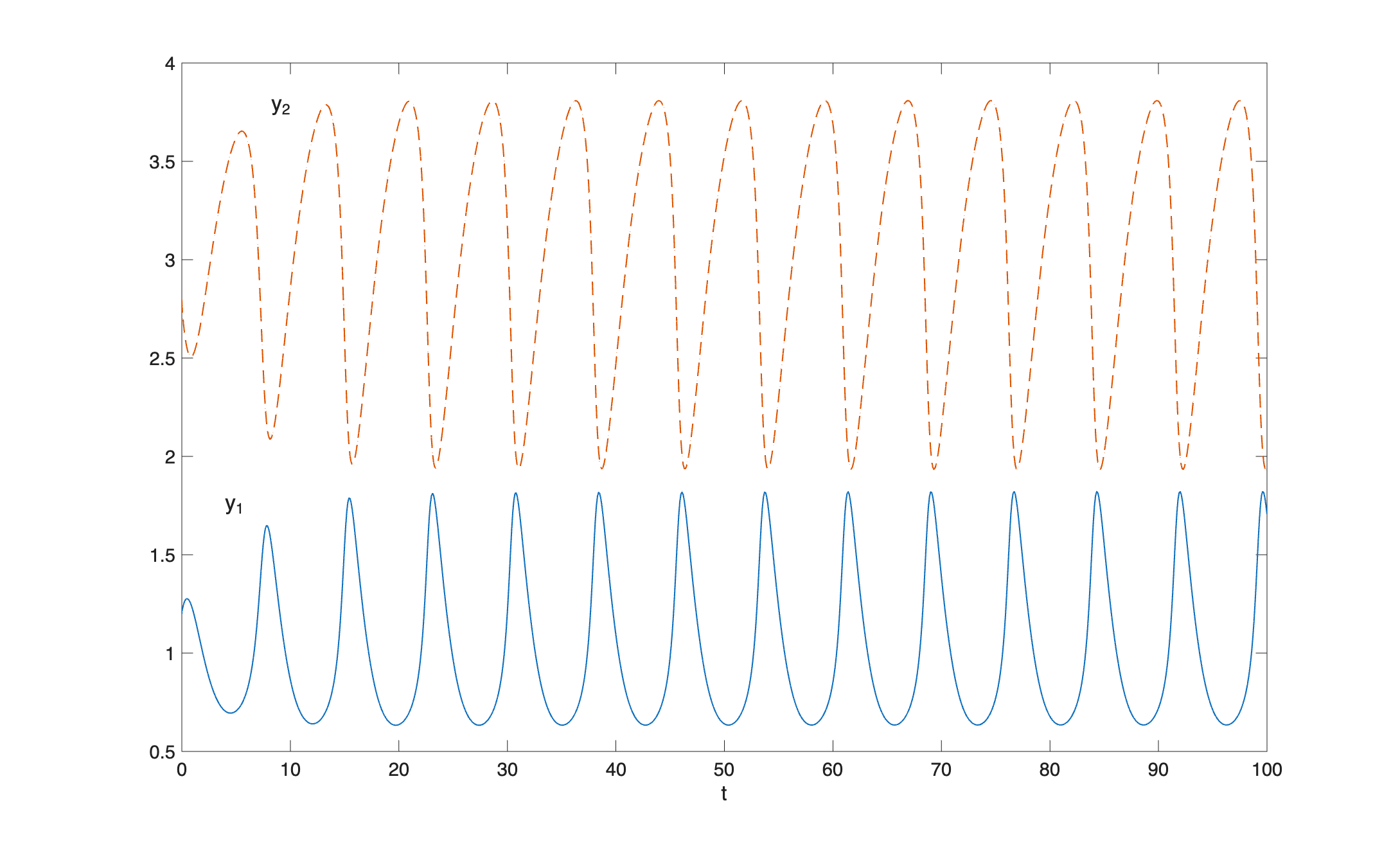
Разработанный метод, основанный на модифицированных полиномах Якоби, обеспечивает спектральную точность и реализован в новом пакете Matlab — fhbvm2.

Несмотря на значительный прогресс в численном решении дробных дифференциальных уравнений, вопросы, связанные с задачами, содержащими производные различных порядков, остаются недостаточно изученными. В настоящей работе, посвященной ‘Recent advances in the numerical solution of multi-order fractional differential equations’, предложено расширение класса методов FHBVM для эффективного и точного решения многопорядковых дробных дифференциальных уравнений. Разработанный подход обеспечивает спектральную точность и реализован в виде Matlab-кода `fhbvm2`, демонстрирующего высокую эффективность. Каковы перспективы применения данного подхода для решения более сложных задач, возникающих в различных областях науки и техники?

---

За пределами классического исчисления: Фрактальная динамика и её математическая изящность

Традиционный дифференциальный и интегральный исчисления, будучи мощным инструментом анализа, часто демонстрирует ограниченность при моделировании систем, обладающих памятью или наследственными свойствами. Это связано с тем, что классическое исчисление предполагает локальность — текущее состояние системы определяется исключительно текущими условиями. Однако, многие реальные процессы, такие как вязкоупругая деформация материалов, распространение тепла в неоднородных средах или динамика популяций, зависят от всей предшествующей истории. В таких случаях, применение стандартных дифференциальных уравнений может приводить к неточным или упрощенным результатам, не отражающим всю сложность происходящих явлений. Например, при описании ползучести материала, стандартное дифференциальное уравнение не учитывает влияние предыдущих деформаций на текущую. Неспособность классического подхода адекватно описывать такие системы стимулировала развитие альтернативных математических инструментов, способных учитывать «память» и наследственность, открывая новые возможности для более точного моделирования и прогнозирования поведения сложных систем.

Дробные производные представляют собой мощный математический аппарат, позволяющий учитывать эффекты памяти и наследственности в динамических системах. В отличие от классического исчисления, где производная отражает мгновенное изменение, дробные производные обобщают эту концепцию, позволяя учитывать влияние прошлых состояний на текущее поведение системы. Это достигается за счет использования нецелых порядков дифференцирования, что позволяет более точно описывать процессы, где изменения происходят не скачкообразно, а с некоторой задержкой или инерцией. Например, при моделировании вязкоупругих материалов или процессов переноса с памятью, дробные производные позволяют получить результаты, значительно лучше соответствующие экспериментальным данным, чем традиционные подходы. Такой подход открывает возможности для более реалистичного моделирования сложных систем в различных областях науки и техники, включая физику, биологию, экономику и инженерию, позволяя уловить нюансы, которые упускаются при использовании классического анализа, например, описывая процессы, где $D^{\alpha }u(t)$ отражает изменение функции $u(t)$ с учетом истории её значений.

Способность учитывать влияние прошлых состояний на текущее поведение системы является ключевой в моделировании сложных процессов. В отличие от классического исчисления, где производная описывает мгновенное изменение, дробные производные позволяют учесть “память” системы, интегрируя историю её развития в текущее состояние. Это особенно важно при анализе явлений, где наблюдается зависимость от предыдущих этапов — например, в реологии материалов с вязкоупругими свойствами, при описании процессов переноса тепла в средах с памятью или при моделировании динамики популяций, где численность на текущий момент зависит от прошлых поколений. Такой подход позволяет создавать более точные и реалистичные модели, способные предсказывать поведение систем, для которых традиционные методы оказываются недостаточно адекватными. В результате, дробное исчисление открывает новые возможности для исследования и управления сложными системами в различных областях науки и техники, позволяя учитывать не только текущие факторы, но и накопленный опыт системы.

Для точного прогнозирования поведения сложных систем, описываемых дробными дифференциальными уравнениями, критически важны надежные численные методы решения. В отличие от традиционных дифференциальных уравнений, дробные уравнения учитывают эффекты памяти и наследуемости, что позволяет более реалистично моделировать процессы, зависящие от предшествующих состояний. Разработка и применение эффективных численных алгоритмов, способных адекватно аппроксимировать решения этих уравнений, является ключевой задачей в таких областях, как физика полимеров, реология, биофизика и финансы. Точность этих решений напрямую влияет на надежность предсказаний и понимание динамики исследуемых систем, особенно в случаях, когда классические подходы оказываются недостаточными. Например, при моделировании диффузии в пористых средах или распространения болезней, учет дробной динамики позволяет получить результаты, более соответствующие реальным наблюдениям, чем при использовании стандартных моделей, основанных на целых производных, таких как $\frac{d^{2}u}{d{t}^2}$.

Сложность многопорядковых ФДУ и вызовы численного анализа

Многопорядковые дробные дифференциальные уравнения (ДДУ) характеризуются повышенной сложностью вследствие наличия нескольких порядков дробного дифференцирования. В отличие от уравнений с целыми порядками производных, где решение зависит только от текущего состояния системы, в многопорядковых ДДУ решение определяется историей процесса, учитывая влияние производных различных порядков. Например, уравнение может содержать как $D^{\alpha }u(t)$, так и $D^{\beta }u(t)$, где $\alpha \ne \beta$ — порядки дробных производных. Это приводит к усложнению математического аппарата и требует применения специализированных методов для анализа и решения таких уравнений, поскольку стандартные численные схемы, разработанные для целых порядков, оказываются неэффективными или приводят к неточным результатам.

Традиционные численные методы, разработанные для дифференциальных уравнений целого порядка, испытывают трудности при решении дробных дифференциальных уравнений из-за их нелокального характера и наличия сингулярных ядер. В отличие от уравнений целого порядка, где производная в данной точке зависит только от значений функции в этой точке и её окрестности, дробные производные учитывают историю функции на всем интервале определения. Это приводит к интегральным представлениям дробных производных, содержащим сингулярные ядра, такие как $\frac{1}{\Gamma (1-\alpha )}$, где $\alpha$ — порядок производной. Такие ядра вызывают значительные вычислительные сложности при использовании стандартных дискретизаций и требуют специальных подходов для обеспечения устойчивости и точности численных решений. Кроме того, нелокальность дробных производных требует обработки информации о функции на всем интервале, что увеличивает объем вычислений и потребность в памяти.

Для эффективного и точного решения многопорядковых ФУР требуются специализированные численные методы, учитывающие особенности дробного исчисления. Традиционные подходы, разработанные для уравнений с целыми порядками производных, часто демонстрируют низкую точность и/или вычислительную эффективность при работе с нелокальными ядрами и сингулярностями, характерными для дробных производных. К таким методам относятся, например, методы конечных разностей с использованием весов, основанных на функции ядра, или спектральные методы, адаптированные для дробных операторов. Важным аспектом является выбор схемы дискретизации, обеспечивающей устойчивость и достаточную скорость сходимости, а также корректная обработка граничных условий и начальных данных, специфичных для многопорядковых ФУР. Примером является использование $\alpha$-численных схем, адаптированных для различных порядков дробной производной, или методы, основанные на преобразовании Лапласа и численном обращении преобразования.

Разработка надежных и масштабируемых численных методов имеет решающее значение для раскрытия полного потенциала дробного исчисления в моделировании сложных систем. Традиционные алгоритмы часто неэффективны при работе с дробными производными, требуя специализированных подходов, способных учитывать нелокальность и особенности дробных операторов. Масштабируемость методов важна для решения задач, возникающих в различных областях, таких как динамика популяций, реология, электрохимия и финансовое моделирование, где сложные взаимодействия и эффекты памяти часто встречаются. Повышение точности и эффективности численных решений позволит применять дробные модели к более реалистичным и крупномасштабным задачам, открывая новые возможности для анализа и прогнозирования поведения сложных систем. Дальнейшие исследования в этой области направлены на разработку адаптивных методов, которые могут автоматически оптимизировать параметры численного решения в зависимости от характеристик конкретной задачи, а также на использование параллельных вычислений для ускорения процесса моделирования.

FHBVM2: Спектральное решение для многопорядковых дробных уравнений

Расширенный метод Fractional HBVM (FHBVM2) использует спектральную точность при решении многопорядковых дробных дифференциальных уравнений ($FDE$) посредством разложения в ряды полиномов Якоби. Данный подход позволяет аппроксимировать решение $FDE$ с высокой точностью, представляя его в виде суммы произведений полиномов Якоби и соответствующих коэффициентов. Спектральная точность достигается за счет использования глобальной аппроксимации, в отличие от локальных методов, что позволяет достичь высокой скорости сходимости и точности решения даже при сложных граничных условиях и негладких ядрах. Эффективность метода обусловлена выбором базиса, который оптимально подходит для аппроксимации функций, возникающих в задачах с дробными производными.

Метод FHBVM2 эффективно дискретизирует дробные производные посредством использования квадратур Гаусса-Якоби и усовершенствованной реализации квадратур Якоби-Пиньейро. Квадратуры Гаусса-Якоби обеспечивают высокую точность интегрирования функций, взвешенных полиномами Якоби, что критично для представления дробных операторов. Усовершенствованная реализация квадратур Якоби-Пиньейро позволяет эффективно вычислять сингулярные интегралы, возникающие при дискретизации дробных производных, особенно в случаях негладких ядер. Данный подход позволяет точно аппроксимировать дробные производные порядка \alpha > 0 путем преобразования интегрального представления в конечную сумму, что значительно снижает вычислительные затраты по сравнению с другими методами.

Метод FHBVM2 обеспечивает высокую точность при решении дробных дифференциальных уравнений даже при наличии комплексных порядков дифференцирования и негладких ядер. Точность достигается за счет использования спектральных разложений на основе полиномов Якоби, что позволяет эффективно аппроксимировать дробные производные. В частности, метод демонстрирует устойчивость и конвергенцию при решении задач, где порядок дробной производной является комплексным числом или ядро содержит разрывы, что является сложной задачей для многих традиционных численных методов. Это делает FHBVM2 применимым к широкому классу задач, возникающих в различных областях науки и техники, где встречаются подобные типы уравнений.

Реализация FHBVM(22,22) представляет собой конкретный пример практической применимости метода для решения многопорядковых дробных дифференциальных уравнений. Данная конфигурация использует 22 узла Гаусса-Якоби для аппроксимации как дробной производной, так и интеграла, что обеспечивает заданную точность решения. Выбор 22 узлов демонстрирует компромисс между вычислительной сложностью и требуемой точностью, позволяя эффективно решать задачи с 0 < \alpha \le 2 и сложными ядрами. Результаты численных экспериментов с FHBVM(22,22) подтверждают вычислительную целесообразность и стабильность метода для широкого класса задач.

Валидация и производительность: Точность и эффективность на практике

Результаты исследований демонстрируют, что метод FHBVM2 обеспечивает спектрально точные решения для многопорядковых дробных дифференциальных уравнений (ДДУ). Это означает, что погрешность вычислений уменьшается экспоненциально с увеличением числа шагов дискретизации, что позволяет получать высокоточные результаты даже при решении сложных задач. Подтвержденный высокий уровень точности особенно важен при моделировании физических процессов, где даже незначительные ошибки могут приводить к существенным отклонениям в прогнозах. Спектральная точность FHBVM2 достигается за счет использования специальной аппроксимации и тщательно разработанной процедуры решения $ДДУ$, что делает его надежным инструментом для численного анализа.

Эффективность разработанного метода характеризуется временем выполнения расчетов, которое сопоставимо или превосходит показатели существующих подходов к решению аналогичных задач. Исследования показали, что для решения $\alpha$-порядковых дифференциальных уравнений в частных производных, метод демонстрирует высокую производительность, позволяя получать результаты за сравнимое или меньшее время, чем при использовании традиционных численных методов. Это особенно важно при моделировании сложных динамических систем, где скорость вычислений является критическим фактором, и позволяет исследователям и инженерам проводить более глубокий анализ и оптимизацию моделей.

Сочетание высокой точности и эффективности делает FHBVM2 ценным инструментом для исследователей и инженеров, работающих в области дробной динамики. Данный метод позволяет получать спектрально точные решения для уравнений дробного порядка, что особенно важно при моделировании сложных систем, где традиционные численные методы оказываются недостаточно точными или требуют чрезмерных вычислительных ресурсов. Благодаря своей эффективности, FHBVM2 предоставляет возможность решать задачи, которые ранее были недоступны из-за ограничений по времени и вычислительной мощности, открывая новые перспективы для исследований в различных областях, таких как физика, биология, инженерия и финансы. Возможность быстрого и точного моделирования дробных процессов делает FHBVM2 незаменимым инструментом для анализа и прогнозирования поведения сложных систем, что способствует развитию новых технологий и инноваций.

Представленный Matlab-код, реализующий метод FHBVM2, демонстрирует превосходство над существующими численными кодами при решении задач на дробные дифференциальные уравнения. Сравнительный анализ показывает, что FHBVM2 обеспечивает не только более высокую точность получаемых решений, но и превосходит конкурирующие методы по скорости вычислений. Это достигается за счет оптимизированной реализации алгоритма, позволяющей эффективно использовать вычислительные ресурсы и минимизировать время, необходимое для получения результата. Данное сочетание высокой точности и производительности делает FHBVM2 ценным инструментом для специалистов, работающих в области дробной динамики и требующих надежных и быстрых численных решений.

Исследование, представленное в данной работе, демонстрирует стремление к математической строгости в решении сложных задач. Разработка метода для численного решения многопорядковых дробных дифференциальных уравнений подчеркивает важность поиска элегантных и доказуемых решений. Как говорил Пётр Капица: «В науке нет места случайностям, только математическая красота и логика». Действительно, предложенный подход, основанный на спектрально точных методах и полиномах Якоби, стремится к исключению приближений и обеспечению надежных результатов, что особенно важно при моделировании сложных систем, где точность является критическим параметром. Разработанный Matlab-код `fhbvm2` является воплощением этой дисциплины, предоставляя инструмент для верификации и подтверждения математической корректности полученных решений.

Куда Далее?

Представленные результаты, безусловно, расширяют инструментарий для решения уравнений дробного порядка, однако не следует забывать старую истину: оптимизация без анализа — самообман и ловушка для неосторожного разработчика. Эффективность предложенного подхода в решении многопорядковых уравнений, хотя и продемонстрирована, требует более глубокого исследования в условиях, приближенных к реальным физическим задачам. Простое достижение спектральной точности на тестовых функциях не гарантирует устойчивость алгоритма при столкновении с данными, содержащими шум или неточности.

Дальнейшие исследования, представляется, должны быть направлены на разработку адаптивных алгоритмов, способных автоматически определять оптимальный порядок аппроксимации и выбирать наиболее подходящие полиномы Якоби для конкретной задачи. Не менее важным представляется вопрос о расширении области применимости метода на уравнения с нелокальными граничными условиями, которые часто встречаются в задачах диффузии и волновой динамики.

В конечном счете, истинная проверка эффективности любого численного метода — это его способность предоставить не просто «число», а осмысленное решение, согласующееся с фундаментальными законами природы. Достижение этой цели требует не только математической элегантности, но и глубокого понимания физической сути решаемой задачи.

---

Оригинал статьи: https://arxiv.org/pdf/2512.04737.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/