Статьи QuantRise
Экзотические разложения: новые грани цилиндрической алгебры
Автор: Денис Аветисян
В статье представлены конкретные примеры в ℝ⁴, опровергающие устоявшиеся предположения о топологических свойствах клеток цилиндрических алгебраических разложений.
Исследование демонстрирует, что свойство сжимаемости замыканий и регулярность секторов не всегда выполняются для клеток CAD, ставя под сомнение ряд существующих теорий.
Несмотря на широкое применение цилиндрических алгебраических разложений (CAD) в различных областях, от алгоритмической логики до планирования движений роботов, некоторые топологические свойства CAD-ячеек оставались предметом дискуссий. В статье ‘On some Exotic Cylindrical Algebraic Decompositions and Cells’ представлены явные контрпримеры в ℝ⁴, опровергающие ряд гипотез Дж. Х. Давенпорта, А. Локателли и Г. К. Санкарана относительно замкнутости и регулярности CAD-ячеек. Полученные результаты демонстрируют, что предполагаемые топологические свойства, такие как стягиваемость замыканий и регулярность секторов, не всегда выполняются для CAD-ячеек. Какие новые ограничения накладывают эти контрпримеры на построение и анализ CAD, и как это повлияет на будущие исследования в области полуалгебраических множеств?
Фундаментальная Аккуратность: Упорядоченные Разложения
Многие геометрические задачи требуют разбиения пространства на более простые ячейки, однако эффективность и корректность такого подхода напрямую зависят от того, насколько “упорядоченным” является это разбиение. Некорректное или плохо организованное разложение может привести к бесконечным вычислениям или неверным результатам. Поэтому, при разработке алгоритмов для решения геометрических проблем, особое внимание уделяется обеспечению определенных свойств этих разложений, гарантирующих их завершенность и надежность. Такие свойства позволяют эффективно обрабатывать полученные ячейки и получать точные решения, избегая проблем, связанных с неопределенностью или сложностью исходного пространства. Именно поэтому, разработка и анализ методов, обеспечивающих “хорошее поведение” разложений, является фундаментом для множества современных геометрических алгоритмов.
Свойства, такие как конечность замыканий и хорошо очерченные границы, играют фундаментальную роль в обеспечении эффективности геометрических разложений. Когда пространство разбивается на более простые ячейки для анализа, важно, чтобы каждое замыкание ячейки содержало лишь конечное число других ячеек — это свойство, известное как конечность замыканий, предотвращает бесконечные рекурсии и обеспечивает вычислимость. Не менее важно, чтобы границы между ячейками были четко определены и «хорошо очерчены», то есть, чтобы их можно было однозначно определить и обработать алгоритмически. Отсутствие этих свойств может привести к неопределенностям и бесконечным циклам в процессе вычислений, делая разложение бесполезным для решения поставленной задачи. Именно поэтому обеспечение этих характеристик является ключевым этапом в создании надежных и эффективных алгоритмов для геометрических вычислений.
Цилиндрическое алгебраическое разложение (CAD) представляет собой мощный инструмент для декомпозиции пространства на более простые ячейки, что позволяет решать сложные геометрические и алгебраические задачи. Однако эффективность этого метода напрямую зависит от соблюдения определенных фундаментальных свойств, таких как замкнутость и хорошоопределенность границ. Без этих характеристик, декомпозиция может оказаться неполной или неоднозначной, что приведет к ошибкам в вычислениях и неверным результатам. Таким образом, обеспечение этих свойств является критически важным этапом в построении CAD, гарантируя надежность и точность получаемых решений, особенно при работе с системами алгебраических уравнений и неравенств в многомерном пространстве.
Определение Неправильности: Секторы и Эквирегулярность
Сектор, в контексте декомпозиции, представляет собой область, ограниченную функциями, и служит базовым элементом для анализа локального поведения. Данный сектор может быть определен как \{x \in U : f_i(x) \le 0, f_j(x) \ge 0\} , где U — некоторая открытая область, а f_i и f_j — функции, определяющие границы сектора. Использование секторов позволяет рассматривать поведение объекта или функции вблизи определенной точки, изолируя его от влияния других областей декомпозиции. Анализ внутри каждого сектора упрощается за счет локализации, что является ключевым преимуществом данного подхода.
Понятие эквирегулярности, определяющее, ведёт ли себя сектор (область, ограниченная функциями) подобно открытому шару, имеет решающее значение для предсказуемого анализа. Формально, эквирегулярность устанавливается посредством «Гомеоморфизма пар» — математического соответствия, которое демонстрирует, что существует непрерывное и обратимое преобразование между данным сектором и открытым шаром в \mathbb{R}^n. Это означает, что локальное поведение функции в секторе можно изучать, используя известные свойства функций в открытом шаре, что значительно упрощает анализ. Отсутствие такого гомеоморфизма указывает на неэквирегулярность и требует применения более сложных методов.
Отклонения от эквирегулярности, то есть ситуации, когда поведение сектора существенно отличается от поведения открытого шара, приводят к усложнению анализа и могут сделать недействительными стандартные аналитические методы. В частности, это касается тех техник, которые опираются на свойства гладких отображений и локальной линейности. Например, применение стандартных методов дифференциальной топологии или комплексного анализа может давать некорректные результаты при наличии сингулярностей или негладких границ в исследуемом секторе. Оценка степени отклонения от эквирегулярности является ключевым этапом при разработке корректных алгоритмов анализа для подобных случаев, требуя применения более сложных и специализированных подходов.
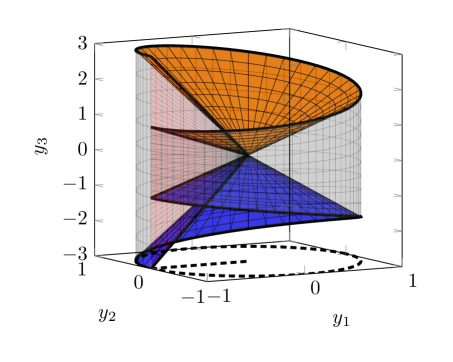
Конструирование Контрпримера: Ячейка Рога
“Ячейка Рога” (Cornet Cell) представляет собой специфическую CAD-ячейку, разработанную для служения основой при построении контрпримеров. Она является фундаментальным строительным блоком в процессе доказательства несостоятельности определенных гипотез в области алгебраической геометрии и теории особенностей. Конкретно, это многообразие, построенное с использованием алгебраических операций над полями и многочленами, и спроектированное таким образом, чтобы демонстрировать поведение, нарушающее ожидаемые свойства регулярности и замкнутости. Конструкция ячейки включает в себя выбор определенных параметров и алгебраических выражений, что позволяет получить контролируемое нарушение требуемых свойств, необходимых для создания валидных контрпримеров.
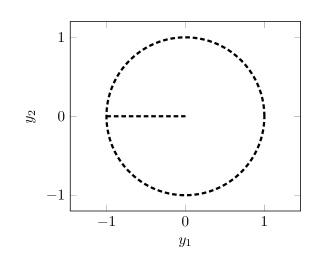
Комбинация “Cornet Cell” и “Slit Disk” позволяет создавать сектора в ℝ⁴, которые однозначно не проходят тест на эквирегулярность. “Slit Disk” встраивается в “Cornet Cell” таким образом, что результирующая структура демонстрирует нарушение условий эквирегулярности, что подтверждается анализом её топологических свойств и метрических характеристик. Именно эта комбинация обеспечивает необходимые условия для построения контрпримеров, опровергающих гипотезы о замкнутости, хорошо окаймленности и регулярности рассматриваемых объектов.
Посредством тщательной разработки ‘Сечения’, определяющего эти сектора, удается продемонстрировать их нерегулярность. Конкретно, контрпримеры строятся в ℝ⁴ и позволяют опровергнуть гипотезы, касающиеся замкнутости, хорошоограниченности и регулярности. Использование специально сконструированного ‘Сечения’ гарантирует, что создаваемые сектора не удовлетворяют критериям регулярности, что, в свою очередь, приводит к построению контрпримеров, доказывающих несостоятельность соответствующих утверждений.
Исследование, представленное в данной работе, демонстрирует, что без чёткого определения свойств полуалгебраических множеств, любое построение цилиндрической алгебраической декомпозиции (CAD) может привести к неопределённостям. В частности, статья конструирует явные контрпримеры в ℝ⁴, опровергающие некоторые существующие предположения о сжимаемости замыканий и регулярности секторов CAD-ячеек. Это подтверждает, что математическая строгость необходима для обеспечения корректности алгоритмов. Как некогда заметил Исаак Ньютон: «Я не знаю, как я выгляжу в глазах мира, но, пока я живу, я желаю быть ничем иным, как скромным ученым». Данная работа придерживается этой скромности, стремясь к доказательству или опровержению гипотез, а не к простому удовлетворению тестовым покрытиям.
Куда Далее?
Представленные в данной работе примеры, демонстрирующие нарушение контрактности замыканий и регулярности секторов в цилиндрических алгебраических разложениях, не являются простым опровержением гипотез. Они обнажают глубинную проблему: стремление к алгоритмической элегантности часто вступает в противоречие с топологической корректностью. Алгоритм, безупречный в своей формальной логике, может порождать структуры, не удовлетворяющие базовым требованиям топологической связности. Это напоминает о необходимости тщательного анализа не только вычислительной сложности, но и топологических свойств результирующих полуалгебраических множеств.
Дальнейшие исследования должны быть направлены на выявление условий, при которых топологические недостатки, продемонстрированные в статье, неизбежны. Необходимо оценить, насколько распространены эти патологии в различных классах полуалгебраических множеств и разработать методы, позволяющие хотя бы частично смягчить их последствия. Вопрос о существовании алгоритмов, гарантированно порождающих “хорошо себя ведущие” ячейки CAD, остается открытым, и его решение, вероятно, потребует отказа от некоторых эвристических упрощений в пользу более строгих математических требований.
В конечном итоге, данная работа служит напоминанием о том, что вычисление — это не просто поиск ответа, но и создание объекта. И этот объект, даже будучи полученным алгоритмически, должен соответствовать базовым математическим принципам. Иначе, красота кода меркнет перед уродством результата.
Оригинал статьи: https://arxiv.org/pdf/2601.09795.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Статья также опубликована на личном сайте автора.