Статьи QuantRise
Подсчет моделей ДНФ: Новый подход к масштабируемым алгоритмам
Автор: Денис Аветисян
Исследователи разработали усовершенствованный алгоритм Монте-Карло для приближенного подсчета моделей дизъюнктивных нормальных форм (ДНФ), значительно повышающий производительность и масштабируемость.
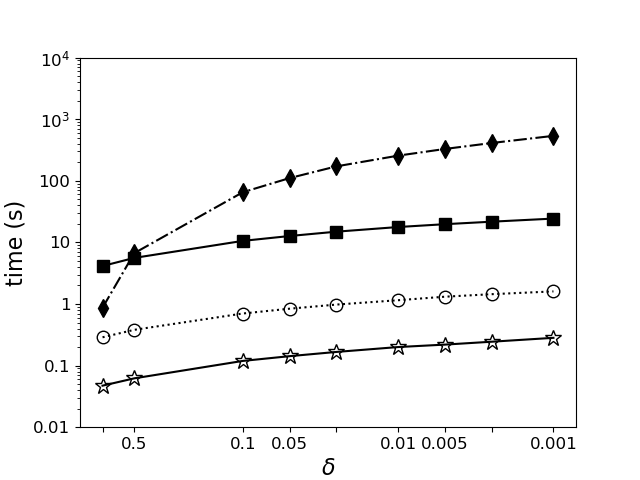
Предлагается адаптивный алгоритм Монте-Карло для приближенного подсчета моделей ДНФ с использованием оптимизированного выбора предложений и параллельной обработки.
Несмотря на вычислительную сложность точного подсчета моделей для дизъюнктивных нормальных форм (DNF), задача остается критически важной в областях вероятностных вычислений и оценки надежности сетей. В работе «Scalable Algorithms for Approximate DNF Model Counting» предложен новый Монте-Карло подход, сочетающий адаптивное правило остановки и оптимизированную оценку формул. Разработанный алгоритм демонстрирует асимптотическую эффективность, превосходя существующие схемы приближенного полиномиального рандомизированного приближения (FPRAS), и обеспечивает масштабируемость до задач с миллионами переменных. Позволит ли данное решение открыть новые горизонты в решении сложных задач комбинаторной оптимизации и искусственного интеллекта?
Задача Подсчета Моделей: Основа Интеллектуальных Систем
Задача подсчета моделей, являющаяся краеугольным камнем вероятностного вывода и искусственного интеллекта, заключается в определении количества наборов значений переменных, при которых булева формула становится истинной. Представьте себе логическое выражение, состоящее из переменных, связанных операциями «И», «ИЛИ» и «НЕ» — задача состоит в том, чтобы перебрать все возможные комбинации значений этих переменных (например, истина или ложь) и посчитать, сколько из них приводят к результату «истина». Это не просто теоретическая головоломка; она лежит в основе многих алгоритмов, используемых для принятия решений в условиях неопределенности, от медицинской диагностики до анализа рисков в финансах. Точное решение этой задачи позволяет оценивать вероятности различных событий и строить более надежные и эффективные системы искусственного интеллекта. По сути, задача подсчета моделей — это фундаментальная операция, лежащая в основе способности машин рассуждать и делать выводы.
Традиционные методы решения задачи подсчета, особенно при работе со сложными логическими формулами, представленными в дизъюнктивной нормальной форме (ДНФ), сталкиваются с проблемой комбинаторного взрыва. В ДНФ, формула состоит из дизъюнкции (логического ИЛИ) конъюнкций (логического И) литералов. По мере увеличения числа переменных и членов в ДНФ, количество возможных комбинаций значений переменных экспоненциально растет. Это приводит к тому, что даже умеренно сложные формулы требуют огромных вычислительных ресурсов и времени для определения числа удовлетворяющих им наборов значений. В результате, стандартные алгоритмы быстро становятся непрактичными для реальных задач, где формулы могут содержать сотни или тысячи переменных, что подчеркивает необходимость разработки более эффективных подходов к решению данной проблемы.
Вычислительная сложность задачи подсчета решений булевых формул напрямую зависит от ширины дизъюнктивных предложений (Clause Width). Чем шире эти предложения, тем быстрее растет число возможных комбинаций значений переменных, что приводит к экспоненциальному увеличению времени вычислений. Это особенно критично для практических приложений, таких как вероятностный вывод в искусственном интеллекте, анализ рисков и верификация сложных систем, где формулы могут содержать тысячи или даже миллионы предложений. Разработка эффективных алгоритмов и методов, способных справляться с широкими предложениями и минимизировать вычислительные затраты, является ключевой задачей для обеспечения масштабируемости и применимости методов подсчета в реальных сценариях. Уменьшение ширины предложений, использование структурных свойств формул и применение параллельных вычислений — это лишь некоторые из подходов, направленных на решение этой важной проблемы.
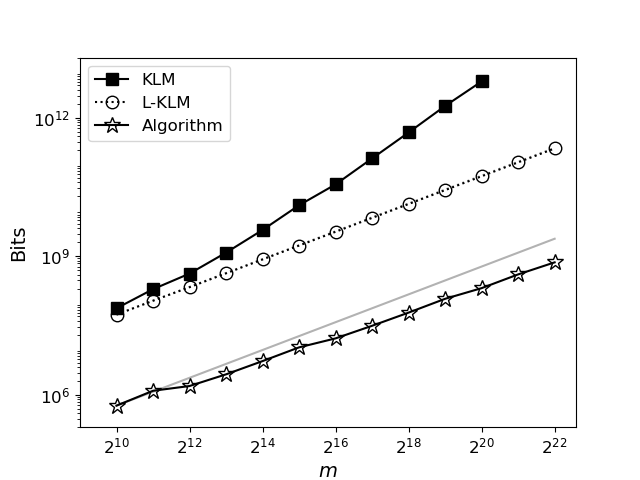
Метод Монте-Карло: Путь к Приближенному Решению
Метод Монте-Карло предоставляет эффективный подход к приближенному подсчету моделей путем оценки доли удовлетворяющих назначений посредством случайной выборки. В основе метода лежит генерация большого числа случайных назначений переменных модели. Доля назначений, удовлетворяющих заданным ограничениям, экстраполируется на все пространство возможных назначений, обеспечивая приближенную оценку количества удовлетворяющих моделей. Точность оценки напрямую зависит от размера выборки: чем больше случайных назначений сгенерировано, тем выше вероятность получения более точного результата. Этот метод особенно полезен для задач, где точный подсчет невозможен из-за экспоненциального роста пространства поиска с увеличением числа переменных.
Метод ленивой выборки (Lazy Sampling) направлен на снижение вычислительных затрат при решении задач модели подсчета. Вместо немедленного назначения значений всем переменным, он откладывает назначение до тех пор, пока это не станет абсолютно необходимым для оценки удовлетворяющего назначения. Это позволяет избежать ненужных вычислений для переменных, которые не влияют на текущую оценку вероятности, и эффективно использовать ресурсы, особенно в случаях, когда большая часть пространства поиска не приводит к удовлетворительным решениям. Отсрочка назначения переменных снижает сложность вычислений и позволяет сосредоточиться на более перспективных ветвях поиска.
Эффективное упорядочение переменных существенно повышает эффективность сэмплирования в методах Монте-Карло, направляя процесс поиска. Оптимальный порядок назначения значений переменным позволяет алгоритму быстрее находить удовлетворяющие условия наборы значений и, следовательно, более точно оценивать долю удовлетворяющих заданным ограничениям состояний. Выбор порядка переменных, влияющий на структуру дерева поиска, может значительно уменьшить дисперсию оценки, особенно в задачах с высокой степенью взаимосвязанности между переменными. Применение эвристик, таких как минимальная степень (minimum degree) или динамический порядок переменных (dynamic variable ordering), позволяет адаптировать порядок назначения значений в процессе сэмплирования, что приводит к более эффективному использованию вычислительных ресурсов и повышению точности приближения.
Оптимизация Сэмплирования с Адаптивным Управлением
Реализация адаптивного правила остановки позволяет алгоритму динамически регулировать количество итераций на основе наблюдаемого прогресса оценки. Вместо фиксированного числа попыток, алгоритм отслеживает изменение оценки и прекращает выполнение, когда достигнута заданная точность или когда дальнейшие итерации не приводят к существенному улучшению результата. Такой подход существенно снижает вычислительные затраты, избегая ненужных вычислений и позволяя алгоритму сосредоточиться на областях поиска, где наблюдается наибольший прогресс. Это особенно эффективно в случаях, когда целевая функция имеет сложную структуру или когда требуется высокая точность оценки.
Оптимизация посредством короткого замыкания (short-circuit evaluation) заключается в прекращении вычисления логических выражений, как только результат становится однозначно определенным. В контексте оценки количества моделей, это означает, что при оценке дизъюнкции условий, если одно из условий признано истинным, дальнейшая проверка остальных условий прекращается. Аналогично, при оценке конъюнкции условий, если одно из условий признано ложным, вычисление прекращается. Данный подход позволяет избежать избыточных вычислений и существенно повысить эффективность алгоритма, особенно при работе с большими наборами данных и сложными логическими выражениями.
Оптимизации, включающие адаптивное правило остановки и короткое замыкание вычислений, значительно повышают скорость сходимости и точность оценки количества моделей. Достигаемая рабочая сложность составляет O(mw log(1/b) / β + mw p log(1/p)), где m — размер модели, w — количество переменных, b — нижняя граница вероятности, β — параметр, определяющий точность, а p — вероятность, связанная с конкретными ограничениями. Данная асимптотическая оценка сложности демонстрирует эффективность предложенных оптимизаций при увеличении размеров модели и количества переменных, позволяя сократить вычислительные затраты по сравнению с наивными подходами.
Нейронные Сети для Ускоренного Подсчета: Новый Горизонт
Подход Neural#DNF использует возможности нейронных сетей для значительного ускорения процесса подсчета моделей. Вместо традиционных, часто вычислительно сложных, методов, Neural#DNF применяет обученную нейронную сеть для аппроксимации функции подсчета, что позволяет получать решения за значительно меньшее время, особенно при работе со сложными логическими формулами. Этот метод эффективно преобразует задачу комбинаторной оптимизации в задачу обучения с учителем, позволяя нейронной сети «научиться» предсказывать количество удовлетворяющих решений без необходимости полного перебора всех возможных комбинаций. Результатом является существенное повышение производительности и возможность решать задачи, которые ранее были недоступны из-за ограничений вычислительных ресурсов.
В отличие от классических методов, требующих экспоненциального времени для решения задач модели подсчета, представленный эвристический подход использует возможности нейронных сетей для значительного ускорения процесса, особенно при работе со сложными формулами. Традиционные алгоритмы часто сталкиваются с трудностями при увеличении числа переменных и ограничений, что делает их непрактичными для масштабных задач. Новый метод позволяет эффективно приближенно оценивать количество решений, обходя вычислительные ограничения, присущие точным алгоритмам. Это достигается за счет обучения нейронной сети, способной выявлять закономерности и взаимосвязи в формуле, что позволяет значительно сократить время вычислений и успешно решать задачи, ранее считавшиеся недоступными для практического применения.
Разработанный алгоритм Монте-Карло демонстрирует сравнимую вычислительную сложность с подходом Neural#DNF, выраженную как O(mw log(1/b) / β + mw p log(1/p)), где m — число клауз, w — максимальная длина клаузы, b — параметр вероятности, а p — вероятность принятия решения. Важно отметить, что, в отличие от многих эвристических методов, новый алгоритм сохраняет теоретические гарантии в отношении наихудшего случая, обеспечивая предсказуемость производительности. Практические испытания подтвердили способность алгоритма эффективно решать задачи, содержащие до 2^{27} переменных, что значительно расширяет возможности решения сложных задач подсчета моделей, ранее недоступных для существующих методов.
Исследование, представленное в статье, демонстрирует стремление к созданию масштабируемых алгоритмов для аппроксимации подсчета моделей в DNF формулах. Подход, основанный на адаптивном правиле остановки и эффективном отборе предложений, позволяет добиться значительного улучшения производительности по сравнению с существующими схемами FPRAS. Этот фокус на оптимизации и элегантности структуры напоминает высказывание Эдсгера Дейкстры: «Простота — это высшая степень совершенства». Действительно, как и в хорошо спроектированном городском ландшафте, где инфраструктура развивается без необходимости перестраивать весь квартал, данная работа подчеркивает важность эволюции структуры алгоритма для достижения оптимальной производительности и масштабируемости.
Куда Далее?
Представленный подход, безусловно, демонстрирует улучшение в масштабируемости приближённого подсчёта моделей для дизъюнктивных нормальных форм. Однако, не стоит забывать: оптимизация скорости — не всегда оптимизация решения. Зачастую, мы стремимся ускорить процесс, не вникая в природу самой задачи. Элегантность алгоритма проявляется не в сложности, а в способности находить простое решение сложной проблемы. Аппроксимация, как и любая абстракция, несёт в себе цену — потерю точности. Вопрос в том, насколько эта цена оправдана в конкретном контексте.
Следующим шагом представляется не столько дальнейшее усовершенствование существующих методов Монте-Карло, сколько поиск принципиально новых подходов. Параллелизм, безусловно, важен, но истинное масштабирование требует отказа от последовательной логики. Необходимо исследовать возможности, заложенные в структурах данных, способных эффективно представлять и обрабатывать огромные объёмы информации. И, конечно, важно помнить, что зависимость от конкретной формы представления формулы — настоящая цена свободы от вычислительных ограничений.
Хорошая архитектура незаметна, пока не ломается. Предложенный алгоритм — лишь один из возможных кирпичиков в построении более надёжной и масштабируемой системы. Истинный прогресс потребует не только технических усовершенствований, но и глубокого философского осмысления самой задачи подсчёта моделей.
Оригинал статьи: https://arxiv.org/pdf/2601.10511.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Статья также опубликована на личном сайте автора.