Геометрия спектра и вычислительная точность

---

В статье представлен обзор взаимосвязи между спектральной геометрией и современными методами численного анализа.

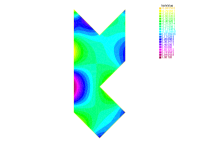
Исследование роли численных методов в изучении собственных значений и функций дифференциальных операторов.

Взаимосвязь между геометрическими свойствами области и спектром оператора, определенного на ней, долгое время оставалась предметом теоретических изысканий. Настоящая работа, озаглавленная ‘At the intersection of Numerical Analysis and Spectral Geometry’, посвящена исследованию роли численных методов в изучении этой взаимосвязи и, в частности, анализу собственных значений и собственных функций дифференциальных операторов. Показано, что современные подходы к дискретизации, разработанные в рамках численного анализа, не только позволяют формулировать гипотезы в спектральной геометрии, но и все чаще используются в качестве инструмента доказательства теорем. Какие новые возможности для развития численного анализа и спектральной геометрии открываются при совместном исследовании этих областей?

---

Спектральная геометрия: За пределами традиционного анализа

Традиционные методы математического анализа зачастую сталкиваются с серьезными трудностями при исследовании областей со сложной геометрией или нерегулярными границами. Классические подходы, основанные на разложении в ряд или использовании дифференциальных уравнений в стандартных координатах, могут оказаться неэффективными или вовсе неприменимыми в таких случаях. Это связано с тем, что стандартные инструменты плохо приспособлены к описанию поведения функций и операторов на областях, где геометрия существенно влияет на их свойства. Необходимость преодоления этих ограничений привела к развитию альтернативных методов, способных учитывать геометрическую сложность домена и обеспечивать решение задач, недоступных для традиционных подходов. В частности, ∂/∂x и ∇² могут иметь неопределенное поведение вблизи сингулярностей, что требует разработки специализированных техник анализа.

Спектральная геометрия представляет собой мощный инструмент, позволяющий установить связь между геометрическими характеристиками области и её спектральными свойствами. В её основе лежит идея о том, что форма и структура объекта проявляются в частотах и модах колебаний, которые можно изучать с помощью операторов, действующих на этой области. Например, собственные значения лапласиана Δ непосредственно связаны с геометрией области, а распределение собственных значений, известное как спектр, несет информацию о её размере, форме и топологии. Изучение этих спектральных характеристик позволяет решать обратные задачи — определять геометрию объекта по его спектру, что находит применение в различных областях, от медицинской визуализации до материаловедения и даже сейсмологии.

Понимание связи между геометрическими свойствами области и её спектральными характеристиками имеет первостепенное значение для решения обратных задач. В частности, спектральная геометрия позволяет восстанавливать форму объекта по его спектру — что особенно актуально в задачах медицинской визуализации, геофизической разведки и неразрушающего контроля. Восстановление формы по спектру представляет собой сложную математическую проблему, требующую глубокого анализа λ -операторов и их собственных функций. Исследование этой взаимосвязи также открывает новые возможности для изучения фундаментальных свойств форм, позволяя определить, какие геометрические характеристики влияют на спектральные свойства, и наоборот, что приводит к более глубокому пониманию математических структур и их приложений в различных областях науки и техники.

Спектральная геометрия представляет собой новаторский подход, объединяющий инструменты математического анализа и геометрии для изучения сложных систем. Данная область позволяет исследовать геометрические свойства объектов через их спектральные характеристики — то есть, через анализ собственных значений и собственных функций соответствующих операторов. Такой симбиоз открывает возможности для решения задач, ранее недоступных традиционным методам, особенно в контексте обратных задач, где необходимо восстановить геометрию по спектральным данным. \Delta u = \lambda u — подобное уравнение, изучаемое в рамках спектральной геометрии, позволяет установить связь между формой области и поведением решения, что находит применение в физике, материаловедении и других областях науки. По сути, спектральная геометрия предлагает новый язык для описания и понимания сложных систем, позволяя взглянуть на геометрию через призму анализа и наоборот.

Вычислительные вызовы и необходимость строгости

Приближение собственных значений и собственных функций с использованием стандартных численных методов, таких как метод конечных элементов (МКЭ) или гранично-элементный метод (ГЭМ), неизбежно вносит погрешности. Эти погрешности обусловлены дискретизацией непрерывной задачи и аппроксимацией бесконечномерного пространства решений конечномерным. В частности, при использовании МКЭ, погрешность возникает из-за аппроксимации геометрии и использования конечного числа элементов, а также выбора аппроксимирующих функций. При использовании ГЭМ погрешности связаны с использованием квадратурных формул и аппроксимацией фундаментального решения. Величина погрешности зависит от размера сетки, порядка аппроксимирующих функций и свойств рассматриваемой задачи, включая ее условленность и сложность геометрии. \lambda_{approx} \neq \lambda_{exact} и \phi_{approx} \neq \phi_{exact} , где λ и φ обозначают собственные значения и собственные функции, соответственно, а индексы “approx” и “exact” указывают на приближенные и точные решения.

Ошибки, возникающие при численном решении задач, могут быть существенными, особенно в случаях, когда задача является плохо обусловленной или имеет сложную геометрию. Плохо обусловленные задачи характеризуются высокой чувствительностью решения к небольшим изменениям входных данных, что приводит к значительной погрешности в результате. Сложная геометрия требует более детальной дискретизации, что увеличивает вычислительную сложность и может приводить к накоплению ошибок округления и аппроксимации. В таких ситуациях, даже небольшие погрешности в исходных данных или алгоритме могут приводить к недостоверным результатам, делая их непригодными для практического применения и требующими дополнительных мер по контролю и снижению погрешности.

Традиционные численные методы, такие как метод конечных элементов (МКЭ) или граничных элементов (ГМЭ), часто не предоставляют строгих оценок погрешности вычислений. Отсутствие таких оценок существенно ограничивает их применение в задачах, где требуется гарантированная точность результатов, например, в критически важных инженерных расчетах или при моделировании физических процессов с высокими требованиями к достоверности. Без возможности количественной оценки погрешности сложно определить, насколько надежны полученные численные решения и соответствуют ли они реальной физической задаче. Это особенно актуально для задач, чувствительных к ошибкам округления или имеющих плохое обусловленность, когда даже небольшие погрешности могут привести к значительным отклонениям в результатах.

Для обеспечения надежности и корректности численных решений, особенно в задачах, чувствительных к погрешностям, необходимо применение методов валидированной вычислительной математики. Данный подход предполагает не только получение численного решения, но и строгую оценку его погрешности, что критически важно для приложений, требующих гарантированной точности. Подтвержденная сходимость различных схем дискретизации, таких как метод конечных элементов (FEM), граничных элементов (BEM) и метод частиц (MPS), является ключевым фактором в обеспечении точности численных приближений и позволяет получить достоверные результаты даже для сложных геометрий и плохо обусловленных задач. Строгий математический анализ сходимости гарантирует, что при достаточном уменьшении шага дискретизации, численное решение сходится к истинному решению задачи.

Валидированная численная математика: Гарантирование точности спектральных решений

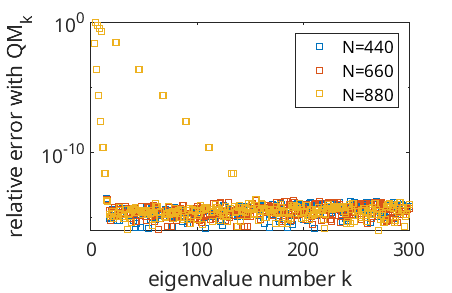
Валидированная численная математика, использующая методы, такие как интервальная арифметика, обеспечивает получение строгих границ погрешностей для численных вычислений. В отличие от традиционных методов, которые предоставляют лишь приближенные значения с оценкой погрешности, валидированная арифметика гарантирует, что истинное решение задачи содержится в полученном интервале. Это достигается путем замены вещественных чисел на интервалы, и выполнения арифметических операций над этими интервалами, что позволяет автоматически отслеживать и накапливать погрешности округления и усечения. В результате, вычисления дают не только приближенное значение, но и гарантированную границу, внутри которой находится точное решение, что критически важно для задач, требующих высокой надежности и сертификации результатов.

Применение методов валидированной нумерики, таких как интервальная арифметика, к спектральным задачам позволяет получать строгие оценки для собственных значений и гарантированное включение собственных функций в заданные интервалы. Это достигается за счет замены операций с вещественными числами операциями над интервалами, что позволяет автоматически отслеживать ошибки округления и моделирования. В результате вычислений получается интервал, который гарантированно содержит истинное значение собственного значения или истинную функцию. Методы включают в себя, например, верификацию интервалов для собственных значений λ и обеспечение, что истинная собственная функция y находится в пределах заданного интервала [y_{min}, y_{max}] для всех x в рассматриваемой области.

Применение методов подтвержденной (валидированной) численной математики расширяет область применимости численных методов в областях, где требуется сертифицированная точность результатов. Это особенно актуально для критически важных инженерных приложений, таких как проектирование авиационных конструкций, анализ устойчивости реакторов, расчеты в ядерной энергетике и моделирование климатических изменений. В этих сценариях недостаточно просто получить численный результат; требуется строгая гарантия того, что результат находится в пределах определенной погрешности, что обеспечивает надежность и безопасность системы. Валидированные численные методы позволяют получать такие гарантии, предоставляя интервальные оценки погрешностей, которые учитывают все источники ошибок, включая ошибки округления и ошибки усечения.

Методы верифицированной численной математики, предоставляя строго доказуемые результаты, устанавливают новый уровень надежности в спектральном анализе. Гарантированные оценки собственных значений, полученные с использованием, например, арифметики интервалов, не просто ограничивают погрешность вычислений, но и позволяют проводить математические доказательства различных гипотез. Так, эти методы успешно применялись для доказательства справедливости таких утверждений, как гипотеза Шиффера и гипотеза Пойа. Кроме того, гарантированные границы собственных значений используются для сертификации оптимизаторов, обеспечивая подтверждение корректности найденных решений и их соответствия заданным критериям. λ — собственные значения, ε — погрешность.

Обратные задачи и форма спектрального пространства

Спектральная геометрия открывает уникальную возможность решения так называемых обратных задач: определение формы области по ее спектру собственных частот. В основе этого подхода лежит тот факт, что форма объекта оказывает непосредственное влияние на характеристики его колебаний, которые, в свою очередь, проявляются в спектре. Исходя из этого, задача восстановления формы сводится к анализу спектральных данных — своего рода «отпечатков» колебаний. \nabla^2 u = \lambda u — это уравнение в частных производных, описывающее колебания в области, где λ — собственные значения, формирующие спектр, а u — соответствующие собственные функции, определяемые формой области. Установление связи между спектром и формой позволяет, теоретически, «услышать» форму объекта, что и является сутью обратной задачи. Решение таких задач имеет важное значение для различных областей науки и техники, от неразрушающего контроля материалов до медицинской диагностики.

Вопрос Каца, сформулированный в середине XX века, представляет собой элегантную, но сложную задачу: возможно ли однозначно восстановить форму двумерного объекта по частотам его колебаний, подобно тому, как можно определить барабан по издаваемым им звукам? Этот вопрос, кажущийся на первый взгляд простым, быстро выявил глубокие математические трудности. Исследования показали, что существуют различные формы, обладающие одинаковым спектром собственных частот — так называемые изоспектральные области. Это означает, что информация, содержащаяся в спектре, недостаточна для однозначного определения геометрии. Поиск условий, при которых восстановление формы возможно, и изучение свойств изоспектральных областей остаются активными областями исследований, демонстрируя, что даже кажущиеся простыми вопросы могут скрывать в себе неожиданную сложность и требовать глубокого математического анализа.

Исследование изоспектральных областей — фигур, имеющих одинаковый спектр собственных частот, — открывает глубокие представления о природе геометрической информации. Удивительно, что совершенно различные по форме области могут производить идентичные звуки, что указывает на то, что спектр не определяет форму однозначно. Эти исследования демонстрируют, что геометрическая информация, содержащаяся в спектре, является неполной, и что существуют ограничения на возможность восстановления формы объекта исключительно по его спектру. Анализ изоспектральных доменов позволяет выявить, какие аспекты формы действительно кодируются в спектре, а какие — теряются, что имеет значение для понимания связи между геометрией и волновыми процессами. Более того, изучение подобных структур помогает разработать алгоритмы, способные находить наиболее вероятные формы объекта, учитывая ограничения, накладываемые изоспектральностью.

Исследования в области обратных задач и спектральной геометрии находят практическое применение в разнообразных научных дисциплинах. В медицинской визуализации, анализ спектральных характеристик позволяет разрабатывать более точные методы неинвазивной диагностики, например, при определении формы и структуры внутренних органов по данным ультразвукового или томографического сканирования. В материаловедении, понимание связи между спектром и формой объекта способствует созданию новых материалов с заданными свойствами, оптимизируя их структуру на микро- и наноуровне. Кроме того, эти исследования имеют ключевое значение для изучения волновых явлений, включая распространение звука, света и сейсмических волн, что позволяет более точно моделировать и прогнозировать поведение волн в различных средах и разрабатывать новые технологии в области связи и обнаружения.

Будущие направления: Оптимизация и сложные геометрии

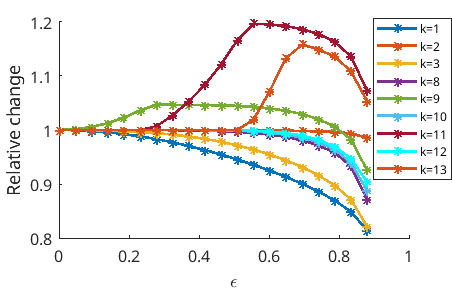
Сочетание спектральной геометрии и методов оптимизации открывает возможности для целенаправленного проектирования областей с заданными спектральными характеристиками. Данный подход позволяет конструировать геометрии, для которых собственные значения оператора Лапласа — определяющие частоты колебаний или распределение энергии — соответствуют заранее установленным требованиям. Исследователи используют алгоритмы оптимизации для итеративной модификации формы области, стремясь достичь желаемого спектра, что находит применение в различных областях, включая акустику, электромагнетизм и даже разработку новых материалов. Например, можно спроектировать камеру резонанса определенной частоты или создать материал с улучшенными оптическими свойствами, манипулируя его геометрией на микроскопическом уровне. \Delta u = \lambda u — это уравнение, описывающее спектральные свойства исследуемой области, где Δ — оператор Лапласа, u — собственная функция, а λ — собственное значение.

Применение методов валидированной вычислительной математики к сложным геометрическим формам, встречающимся в медицинской визуализации и материаловедении, представляет собой важный рубеж в исследованиях. Анализ таких структур требует разработки и использования численных методов, способных точно и надежно решать задачи, связанные с определением собственных значений и спектральных свойств. Особое внимание уделяется проверке результатов вычислений, чтобы гарантировать их соответствие реальным физическим явлениям и избежать ошибок, возникающих из-за ограниченной точности вычислений или неадекватности модели. Развитие этих методов позволит создавать более точные модели и симуляции, что, в свою очередь, откроет новые возможности для диагностики заболеваний, разработки новых материалов и оптимизации инженерных конструкций. Успешное решение этих задач требует тесного сотрудничества между математиками, физиками и специалистами в соответствующих областях применения.

Междисциплинарный подход, объединяющий спектральную геометрию, оптимизационные методы и валидированную вычислительную математику, открывает перспективы для получения новых знаний и стимулирования инноваций в различных областях науки и техники. Подтвержденная сходимость численных методов при уменьшении размера сетки, установленная как посредством теоретического анализа, так и экспериментальной проверки, гарантирует надежность получаемых результатов применительно к сложным геометрическим формам, встречающимся, например, в медицинской визуализации или материаловедении. Такой синергетический эффект позволяет не только решать существующие задачи более эффективно, но и формулировать принципиально новые вопросы, требующие комплексного подхода и открывающие путь к прорывным технологиям.

Исследование взаимосвязи численного анализа и спектральной геометрии демонстрирует стремление к построению математически строгих моделей, что находит отражение в использовании численных методов для проверки гипотез и доказательства теорем. Пусть N стремится к бесконечности — что останется устойчивым? В данном контексте, устойчивость проявляется в точности вычисления собственных значений и собственных функций дифференциальных операторов, независимо от дискретизации, используемой в методе конечных элементов. Как говорил Никола Тесла: «Самое важное — это не то, что мы можем сделать, а то, что мы должны сделать». Эта фраза подчеркивает необходимость поиска фундаментальных истин, а не просто практических решений, что особенно актуально для спектральной оптимизации и валидированной вычислительной математики.

Куда двигаться дальше?

Представленный обзор неизбежно выявляет границы применимости численных методов в области спектральной геометрии. Зачастую, кажущееся подтверждение гипотез посредством численного эксперимента — лишь удобство, а не доказательство. Необходимо помнить, что конечная точность вычислений вносит систематическую ошибку, которую не всегда удается адекватно оценить. Стремление к «достаточно хорошему» решению — компромисс, часто маскирующийся под прогресс.

Перспективным направлением представляется разработка методов верифицируемых вычислений, способных предоставить не просто приближенное значение спектра, но и гарантированные границы погрешности. Игнорирование этой проблемы ведет к накоплению ложных утверждений, которые, будучи замаскированы под математическую строгость, могут затормозить истинное развитие теории. Необходимо отделить математическую элегантность от удобства реализации.

В конечном итоге, истинный прогресс в данной области требует не просто увеличения вычислительной мощности или усовершенствования численных алгоритмов, но и развития более глубокого теоретического понимания спектральных свойств дифференциальных операторов. Численные методы должны служить инструментом для формулировки и проверки гипотез, а не самоцелью. Иначе рискуем построить великолепный замок на песке.

---

Оригинал статьи: https://arxiv.org/pdf/2512.25012.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/