Геометрия вычислений: Новый подход к численному моделированию

---

В статье представлен инновационный метод дискретизации дифференциальных уравнений в частных производных, основанный на использовании метрических свойств пространства вычислений.

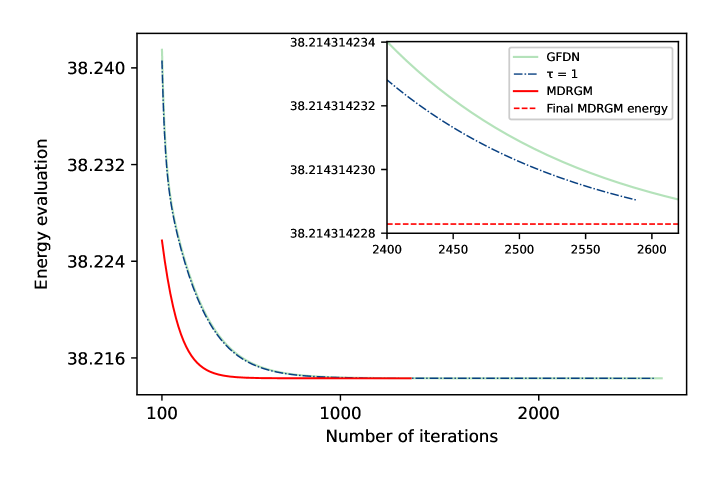
Разработанный подход, применяемый к уравнению Гросса-Питерса, демонстрирует повышенную точность и скорость сходимости при моделировании SO-связанных бозе-эйнштейновских конденсатов.

Эффективное решение многомасштабных дифференциальных уравнений в частных производных часто осложняется вычислительными трудностями и необходимостью высокой точности. В работе ‘Metric-driven numerical methods’ представлен новый подход, основанный на использовании метрически-управляемой дискретизации для вычисления минимизаторов функционалов и решения связанных задач на собственные значения. Показано, что выбор метрики не только ускоряет сходимость итерационных схем, но и позволяет строить аппроксимирующие пространства с улучшенными свойствами, особенно в условиях низкой регулярности или при наличии гетерогенных многомасштабных особенностей. Может ли данный подход стать основой для разработки более эффективных численных методов в различных областях физики и инженерии, включая моделирование конденсированных сред?

---

Понимание Основных Состояний: Ключ к Моделированию Сложных Систем

Многие физические системы, такие как бозе-эйнштейновские конденсаты и сверхтекучие жидкости, описываются сложными нелинейными уравнениями, такими как уравнение Гросса-Питиевского. Эти уравнения возникают из-за взаимодействия между составляющими частицами и отражают фундаментальную сложность коллективного поведения. В отличие от простых гармонических осцилляторов, где решения могут быть получены аналитически, нелинейность в этих системах приводит к появлению широкого спектра явлений, включая самоорганизацию, формирование солитонов и квантовые фазовые переходы. Понимание и моделирование этих систем требует продвинутых математических и вычислительных методов, поскольку даже небольшие отклонения в нелинейных членах уравнений могут привести к экспоненциальному росту ошибок в расчетах и существенно исказить предсказанные свойства вещества. Следовательно, разработка эффективных алгоритмов для решения нелинейных уравнений является ключевой задачей в современной физике конденсированного состояния и квантовой оптике.

Определение точного основного состояния — конфигурации с минимальной энергией — является фундаментальным для понимания поведения сложных физических систем. Именно это состояние определяет стабильность и реакцию системы на внешние воздействия. Представьте себе молекулу или сверхпроводник: их свойства напрямую зависят от того, как электроны распределены в пространстве в состоянии с наименьшей энергией. Неточное определение основного состояния приводит к искажению предсказаний относительно динамики системы, ее спектральных характеристик и даже возможности фазовых переходов. Поэтому поиск и моделирование основного состояния является не просто технической задачей, а необходимым условием для получения достоверной картины поведения сложных материалов и явлений, от $BEC$ до высокотемпературных сверхпроводников.

Традиционные численные методы, применяемые для моделирования сложных систем, зачастую сталкиваются с серьезными трудностями, обусловленными их мультимасштабной природой. Проблема заключается в том, что эти системы характеризуются процессами, протекающими на существенно различающихся пространственных и временных масштабах. Например, для описания турбулентности или поведения Бозе-Эйнштейновского конденсата необходимо одновременно учитывать как макроскопические явления, так и микроскопические флуктуации. Попытки решить соответствующие уравнения, используя стандартные подходы, могут приводить к значительным погрешностям, требующим чрезмерно больших вычислительных ресурсов, либо к полной неспособности получить адекватное решение. В результате, моделирование становится не только трудоемким, но и может давать неверные прогнозы о реальном поведении системы, подчеркивая необходимость разработки новых, более эффективных алгоритмов, способных учитывать мультимасштабность исследуемых процессов и обеспечивать высокую точность и скорость вычислений.

Дискретизация, Управляемая Метрикой: Градиенты Соболева в Действии

В основе численного решения используемой нами схемы лежит дискретизация, управляемая метрикой, с применением специально подобранного градиента Соболева для решения лежащего в основе частного дифференциального уравнения. Этот подход позволяет учитывать геометрические свойства задачи и адаптировать разрешение сетки в соответствии с локальными особенностями решения. Выбор градиента Соболева обусловлен его способностью эффективно представлять и аппроксимировать производные функции, что критически важно для точного решения уравнений в частных производных. Использование метрики в процессе дискретизации позволяет оптимизировать процесс сходимости и уменьшить погрешность численного решения, особенно в областях с высокой кривизной или сложной геометрией. Эффективность данного подхода заключается в адаптивном определении шага дискретизации в зависимости от локальных свойств решения, что позволяет добиться более высокой точности при меньших вычислительных затратах.

В основе предлагаемого подхода лежит использование локализованного ортогонального разложения (LOD-пространства), которое адаптируется к мультимасштабным характеристикам решаемой задачи. LOD-пространство конструируется путем локальной аппроксимации решения в окрестности каждой точки сетки, используя ортогональные базисные функции. Адаптивность достигается за счет изменения размера и формы этих локальных базисов в зависимости от локальной сложности решения, что позволяет эффективно представлять как гладкие, так и сильно осциллирующие участки. Такая локализация снижает вычислительные затраты и обеспечивает более точное приближение, особенно в областях с высокой градиентной структурой, поскольку позволяет использовать более плотную дискретизацию там, где это необходимо, и более разреженную — в областях с меньшими изменениями.

Локализованное ортогональное разложение (LOD) строится в функциональных пространствах, таких как $H^1$ и $L^2$, что обеспечивает математическую строгость и устойчивость численной схемы. Использование этих пространств позволяет корректно определять нормы и обеспечивать сходимость решения, а также гарантирует, что операторы, используемые в дискретизации, являются ограниченными и эллиптическими. Конструкция LOD в рамках $H^1$ пространства обеспечивает учет градиентов решения, что важно для корректного приближения производных, а использование $L^2$ пространства гарантирует, что решение принадлежит пространству квадратично интегрируемых функций, что необходимо для анализа его свойств и оценки погрешности.

Предложенный метод обеспечивает более эффективное и точное представление решения, демонстрируя улучшение скорости сходимости по сравнению со стандартными подходами. В частности, достигается ошибка в норме $H^1$ порядка $O(H^3)$ и ошибка в норме $L^2$ порядка $O(H^4)$, где $H$ представляет собой характерный размер шага дискретизации. Данные оценки ошибок указывают на повышенную скорость сходимости и, следовательно, на возможность получения более точных результатов при заданном уровне дискретизации или, альтернативно, на снижение вычислительных затрат при достижении заданной точности.

Гарантия Качества Решения: Локальные Минимумы и Оптимальность

Для обеспечения достоверности полученного решения проводится строгий анализ его свойств как локального минимума функционала энергии. Это предполагает проверку выполнения как первого, так и второго условий необходимости, связанных с градиентом и гессианом функционала, соответственно. Локальный минимум подразумевает, что малые возмущения аргументов функционала не приводят к существенному снижению его значения. Оценка этих условий является критически важной для подтверждения корректности дискретного решения и демонстрации его сходимости к истинному основному состоянию. Несоблюдение этих условий указывает на возможность существования более оптимальных решений, что ставит под сомнение качество полученного результата.

Для подтверждения локальной минимальности полученного решения необходимо выполнение как первого, так и второго порядковых условий. Первое порядковое условие требует, чтобы градиент функционала, $\nabla F$, был равен нулю в точке локального минимума. Второе порядковое условие, связанное с выпуклостью, требует положительной определенности гессиана функционала, ${\nabla }^{2}F$, в той же точке. Положительная определенность гессиана гарантирует, что найденная точка является точкой локального минимума, а не седловой точкой или максимумом. Оба условия совместно обеспечивают необходимую, но не всегда достаточную, гарантию оптимальности решения.

Производная Фреше играет ключевую роль в определении условий локальной оптимальности и установлении оптимальности решения. В контексте энергетических функционалов, первая производная (градиент) должна быть равна нулю в точке оптимума, что является необходимым, но недостаточным условием. Для обеспечения локальной оптимальности необходимо также, чтобы вторая производная (гессиан) была положительно определенной. Производная Фреше обобщает понятие дифференцируемости и позволяет строго определить эти условия для функционалов, которые могут не быть дифференцируемыми в классическом смысле. Именно использование производной Фреше позволяет корректно анализировать стационарные точки функционала и гарантировать, что найденное решение действительно соответствует локальному минимуму энергии, а не является седловой точкой. В частности, положительная определенность гессиана, вычисленного с использованием производной Фреше, обеспечивает выпуклость функционала в окрестности оптимума, что гарантирует глобальную оптимальность в этой окрестности.

Подтверждение выполнения условий первого и второго порядка, касающихся градиента и гессиана функционала, предоставляет убедительные доказательства того, что полученное дискретное решение является точной аппроксимацией истинного основного состояния. Численные эксперименты демонстрируют улучшение скорости сходимости по сравнению со стандартными методами конечных элементов P1, особенно в задачах с мультимасштабными коэффициентами. Это означает, что предлагаемый подход позволяет достичь более точных результатов за меньшее время вычислений, особенно при решении задач, где коэффициенты существенно меняются в зависимости от масштаба.

Исследование, представленное в данной работе, демонстрирует, что понимание системы требует глубокого изучения её внутренних закономерностей. Как и микроскоп, позволяющий рассмотреть мельчайшие детали объекта, разработанный метрически-ориентированный подход к дискретизации уравнений, в частности уравнения Гросса-Питаевского, позволяет выявить скрытые свойства конденсированных систем. Сергей Соболев однажды заметил: «Математика — это не только язык, но и способ мышления». Эта фраза особенно актуальна здесь, поскольку разработанный метод, основанный на локализованном ортогональном разложении (LOD) и метрически-ориентированной дискретизации, представляет собой логичный и креативный подход к минимизации энергии и повышению точности решения уравнений, раскрывая тем самым новые возможности в исследовании сложных физических явлений.

Куда двигаться дальше?

Представленные здесь методы, ориентированные на метрику дискретизации, открывают возможности для более точного моделирования сложных систем, в частности, уравнений Гросса-Питевского для конденсированных сред Бозе-Эйнштейна. Однако, следует признать, что сама идея «метрики» в контексте численного анализа — это лишь инструмент. Его эффективность напрямую зависит от адекватного выбора метрики и способности выявлять истинные структурные зависимости, скрытые в данных. Необходимо углублённое исследование влияния различных метрических тензоров на стабильность и сходимость численных схем.

Особый интерес представляет расширение подхода, основанного на локальном ортогональном разложении (LOD), на более общие классы дифференциальных уравнений в частных производных. Попытки универсализации LOD могут столкнуться с трудностями, связанными с адаптацией к различным геометриям и граничным условиям. Важно не просто получить «красивый результат», а понять, какие упрощения и приближения были сделаны, и как они влияют на физическую интерпретацию модели.

В конечном итоге, истинный прогресс заключается не в разработке всё более сложных алгоритмов, а в углублении понимания лежащих в основе физических процессов. Каждое изображение, каждое численное решение — это лишь проекция реальности, и задача исследователя — научиться видеть сквозь эту проекцию закономерности, которые определяют поведение системы. Поиск этих закономерностей — это и есть подлинный вызов.

---

Оригинал статьи: https://arxiv.org/pdf/2512.10083.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/