Квантовые технологии
Граненая точность: Квантовые сенсоры на основе графена и функция Ламберта W
Автор: Денис Аветисян
Новый теоретический подход, основанный на свойствах функции Ламберта W, позволяет значительно повысить чувствительность квантовых сенсоров, изготовленных из графеновых нанолент.
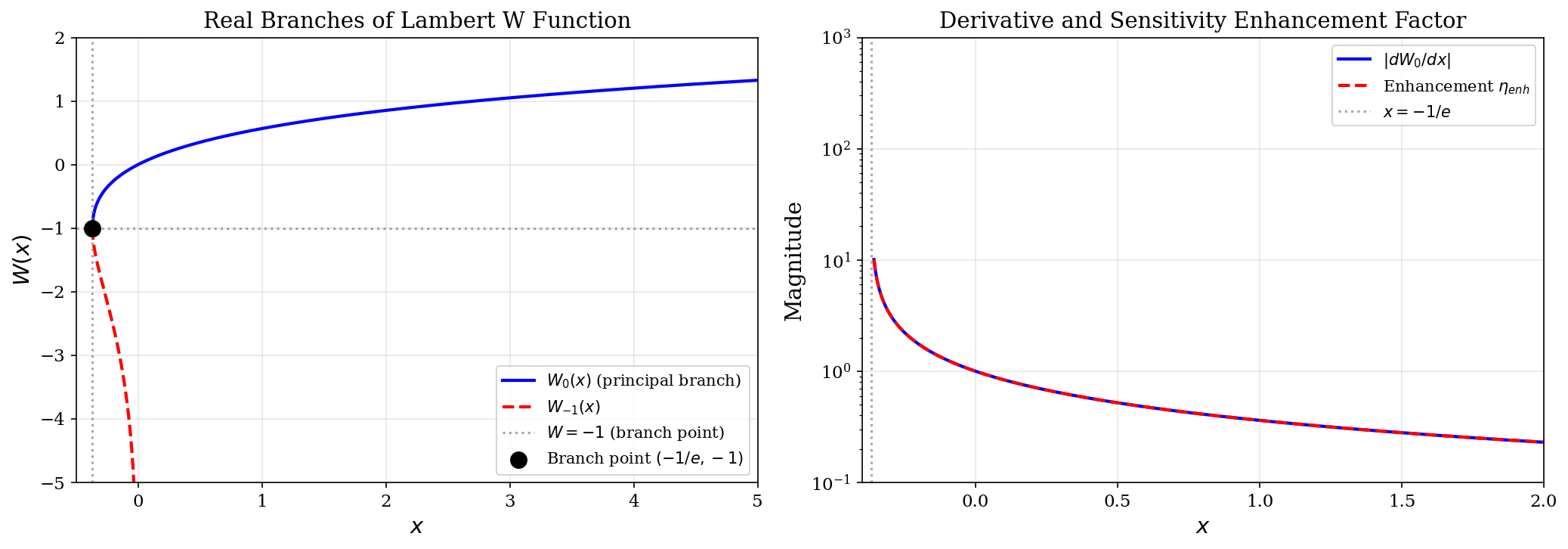
Разработана унифицированная теоретическая база для оптимизации дизайна квантовых сенсоров на основе графеновых нанолент, использующая особенности функции Ламберта W вблизи точки ветвления.
Несмотря на перспективность графеновых нанолент в качестве квантовых сенсоров, оптимизация их чувствительности остается сложной задачей. В работе «Lambert W Function Framework for Graphene Nanoribbon Quantum Sensing: Theory, Verification, and Multi-Modal Applications» предложен строгий математический подход, связывающий квантовое сенсорирование на основе графеновых нанолент с функцией Ламберта W, что позволяет получить аналитические решения для описания квантового замыкания. Показано, что работа вблизи точки ветвления функции Ламберта W обеспечивает значительное усиление чувствительности, а разработанная теоретическая база подтверждается численными расчетами и экспериментальными данными для различных применений — от биомедицинского анализа до мониторинга окружающей среды. Сможет ли предложенный фреймворк стать основой для создания нового поколения высокочувствительных графеновых квантовых сенсоров с предсказуемыми характеристиками?
Квантовое Заточение: Пределы Традиционных Решений
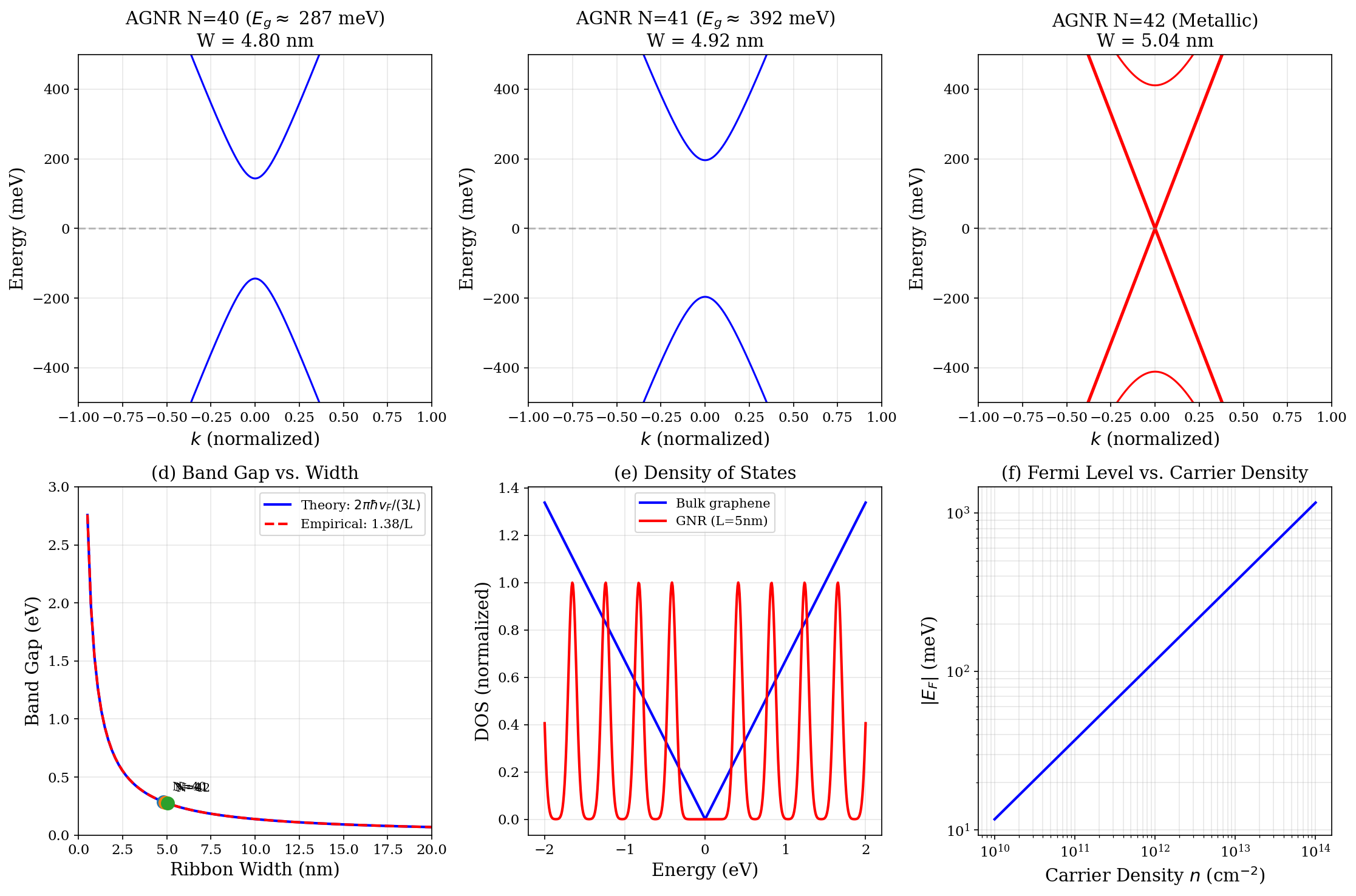
Для адекватного описания поведения электронов в наноструктурах, таких как наноленты из графена, требуется решение сложных задач квантовой механики. В отличие от макроскопических систем, где классическая физика дает достаточно точные результаты, в наномасштабе размеры сопоставимы с длиной волны электрона, что приводит к проявлению волновых свойств и квантовым эффектам. Например, решение уравнения Шредингера для электрона в потенциальной яме — базовой модели для понимания поведения электронов в нанолентах — приводит к сложным трансцендентным уравнениям, требующим численных методов для получения решений. Такое описание необходимо для прогнозирования ключевых свойств материалов, таких как ширина запрещенной зоны E_g, которая напрямую влияет на оптические и электронные характеристики и, следовательно, определяет возможности применения в сенсорах и других наноэлектронных устройствах.
При моделировании поведения электронов в наноструктурах, таких как наноленты из графена, возникают сложные квантовомеханические уравнения. В частности, при рассмотрении потенциальной ямы конечной ширины, описывающей квантование электронов, получаются трансцендентные уравнения, не имеющие аналитических решений в общем случае. Традиционные численные методы, используемые для их решения, часто сталкиваются с трудностями сходимости и требуют значительных вычислительных ресурсов, особенно при стремлении к высокой точности. Это затрудняет точное предсказание ключевых свойств нанолент, например, ширины запрещенной зоны E_g, что критически важно для разработки эффективных сенсоров и других наноэлектронных устройств. Поиск новых, более эффективных методов решения этих уравнений является актуальной задачей современной физики твердого тела.
Ограничения, возникающие при решении сложных квантово-механических задач для наноструктур, таких как графенные наноленты, существенно затрудняют точное предсказание их ключевых свойств, в частности, ширины запрещенной зоны E_g. Эта величина является критически важной для разработки высокочувствительных сенсоров, поскольку определяет спектральные характеристики поглощения и излучения материала. Неточность в определении ширины запрещенной зоны напрямую влияет на эффективность и селективность сенсорных устройств, ограничивая их возможности в обнаружении определенных веществ или изменений окружающей среды. Таким образом, преодоление этих вычислительных сложностей необходимо для создания нового поколения сенсоров с улучшенными характеристиками и расширенным функционалом.
Функция Ламберта W: Аналитический Ключ к Квантовому Контролю
Функция Ламберта W предоставляет точное аналитическое решение трансцендентных уравнений, возникающих в модели конечной потенциальной ямы, и, как следствие, в графеновых нанолентах (GNR). Трансцендентные уравнения обычно не имеют решений в замкнутой форме, что требует использования численных методов. Однако, функция Ламберта W, определяемая как решение уравнения W(x)e^{W(x)} = x, позволяет выразить решения этих уравнений в аналитическом виде. В контексте модели конечной потенциальной ямы это позволяет получить точные выражения для энергетических уровней и волновых функций электронов, что критически важно для понимания электронных свойств GNR, где квантовое confinement играет ключевую роль.
Функция Ламберта W позволяет точно определить ширину запрещенной зоны E_g в квантовых структурах, таких как квантовые ямы и графеновые наноленты. Связь между квантовым ограничением и энергетическими уровнями описывается трансцендентными уравнениями, решение которых напрямую определяет величину E_g. Использование функции Ламберта W обеспечивает аналитическое выражение для E_g, зависящее от параметров ограничения и материала, что позволяет проводить точный расчет ширины запрещенной зоны без необходимости применения численных методов.
Использование аналитического подхода, основанного на функции Ламберта W, позволяет избежать необходимости в ресурсоемких численных методах при решении уравнений, возникающих при моделировании квантовых структур, таких как квантовые ямы и графеновые наноленты. Традиционные численные методы, требующие значительных вычислительных мощностей и времени, заменяются точным аналитическим решением. Это обеспечивает существенное преимущество в процессе проектирования и оптимизации устройств на основе этих структур, позволяя быстро и эффективно исследовать различные конфигурации и параметры для достижения желаемых характеристик, например, ширины запрещенной зоны E_g. Сокращение времени вычислений и повышение точности результатов является ключевым фактором для практического применения и масштабирования технологий на основе графена.
Усиление Чувствительности Благодаря Физике Точки Ветвления
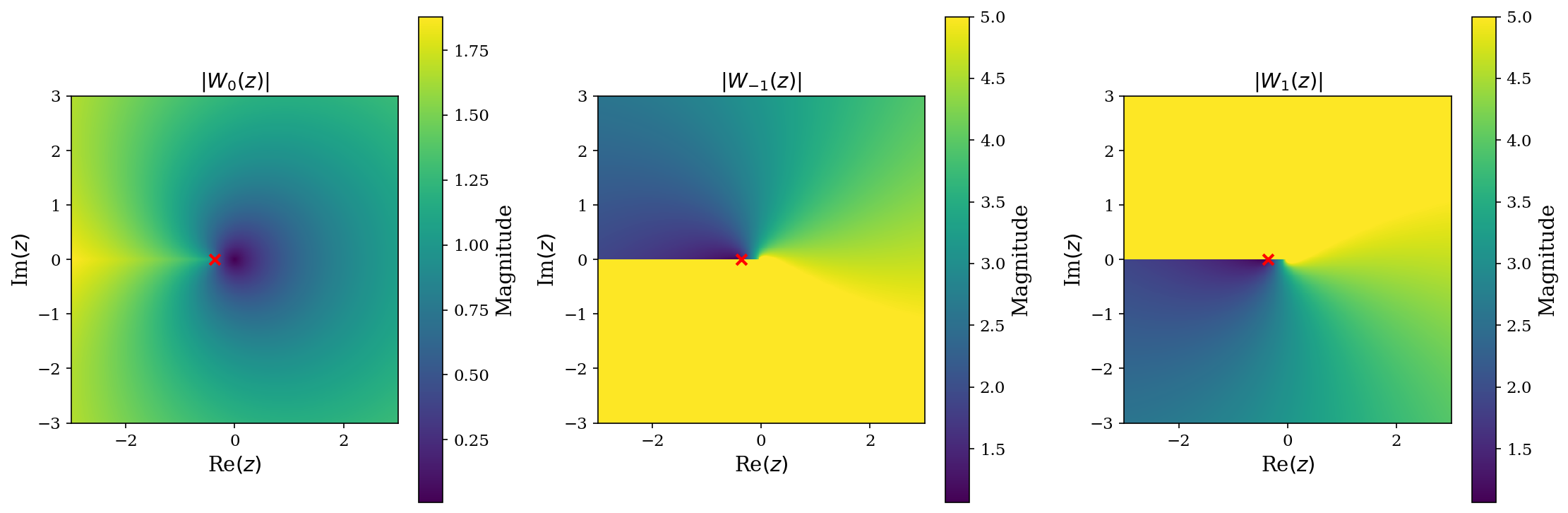
Функция Ламберта W характеризуется точкой ветвления — сингулярностью, оказывающей существенное влияние на её поведение и, что критически важно, на чувствительность GNR-сенсоров. Данная точка ветвления представляет собой особенность функции, где её значение становится мультизначным. В окрестности этой точки небольшие изменения энергетических уровней приводят к значительным изменениям волновой функции, что обуславливает усиление отклика сенсора. Положение точки ветвления определяется параметрами системы и позволяет точно настроить сенсор на максимальную чувствительность к целевым аналитам. Математически, точка ветвления возникает при W(x) = -1/e, что связано с особенностью комплексной плоскости и влияет на решение трансцендентного уравнения, используемого в моделировании GNR-сенсоров.
Вблизи точки ветвления функции Ламберта W небольшие изменения уровней энергии приводят к существенным изменениям волновой функции, что усиливает отклик сенсора. Это связано с тем, что в данной области функция демонстрирует повышенную чувствительность к вариациям входных параметров. Математически, это проявляется в резком изменении значения функции W(z) при незначительных отклонениях z от критической точки. В контексте графеновых наноленточных (GNR) сенсоров, даже минимальные флуктуации энергии, вызванные взаимодействием с аналитом, приводят к пропорционально большему изменению вероятности туннелирования электронов, что и обеспечивает усиление сигнала.
Повышенная чувствительность, обусловленная физикой точки ветвления, позволяет детектировать незначительные изменения окружающей среды с предельной чувствительностью, достигающей 1 фг/мл, 1 ч.з.д. (ppb), 1 фМ и 1 мК в различных режимах сенсорики. Данные показатели соответствуют пределам обнаружения для концентраций вещества в диапазоне фемтограмм на миллилитр, частей на миллиард, фемтомоляр и милликельвинов соответственно, что делает данную технологию применимой для высокоточного анализа в различных областях, включая биосенсорику и мониторинг окружающей среды.
Графеновые Наноленты: Многомодальная Платформа для Сенсорики
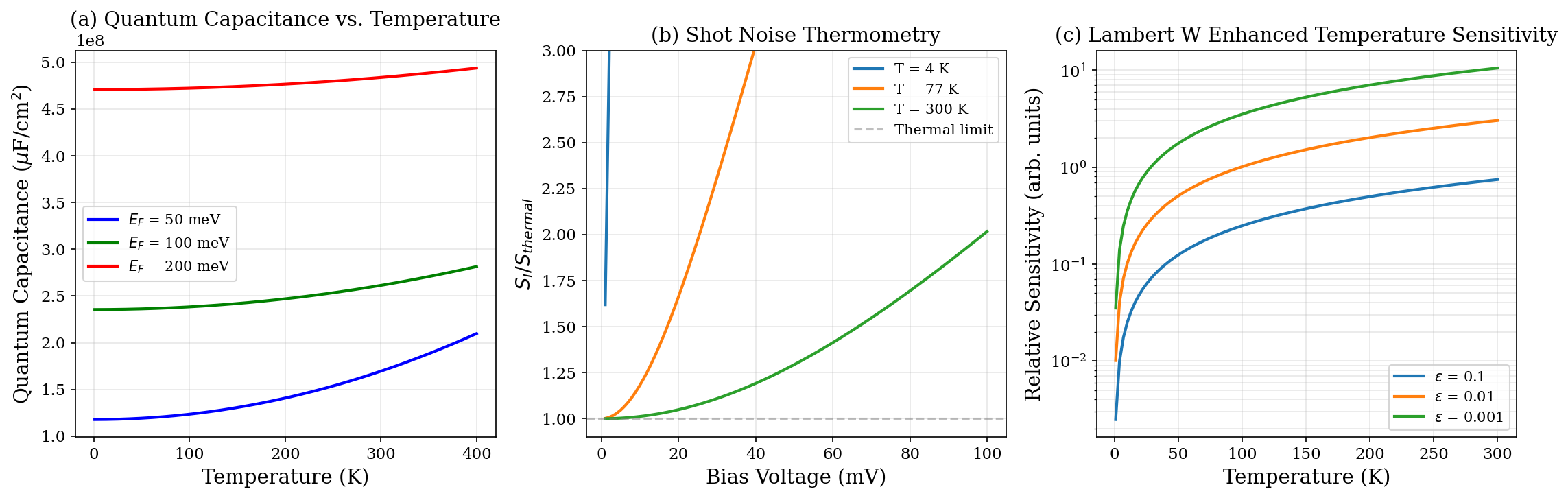
Графеновые наноленты представляют собой перспективную платформу для создания сенсоров различного назначения, охватывающих измерение температуры, деформации и химического состава. Возможность точного определения характеристик этих материалов, в частности, с использованием аналитического аппарата функции Ламберта W, позволяет создавать сенсоры с повышенной чувствительностью и разрешающей способностью. Этот математический инструмент обеспечивает точное моделирование электронных свойств графеновых нанолент, что критически важно для оптимизации их работы в качестве датчиков. Благодаря уникальным электронным свойствам графена, включая высокую подвижность носителей заряда, такие сенсоры демонстрируют превосходную производительность и могут быть адаптированы для широкого спектра приложений, от мониторинга окружающей среды до биомедицинских исследований.
Высокоточные измерения квантовой ёмкости и шумового тока, в сочетании с высокой скоростью Ферми в графене, позволяют значительно улучшить характеристики и разрешение сенсоров на основе графеновых нанолент. Квантовая ёмкость, определяющая способность накапливать заряд, в графене проявляется из-за его двумерной структуры и квантово-механических эффектов, что делает её особенно чувствительной к изменениям окружающей среды. Шумовой ток, возникающий из-за дискретной природы заряда, предоставляет дополнительную информацию о проводимости и позволяет обнаруживать даже самые слабые сигналы. Благодаря высокой скорости Ферми, электроны в графене перемещаются с большой скоростью, что способствует быстрой реакции сенсора и повышает его чувствительность к изменениям параметров окружающей среды, таким как температура, деформация или химический состав. Такое сочетание факторов открывает возможности для создания высокочувствительных и быстродействующих сенсоров нового поколения.
Исследования графеновых нанолент показали, что чувствительность сенсоров обратно пропорциональна квадратному корню из расстояния до точки ветвления — δ^{-1/2}. Этот принцип позволяет значительно усилить сигнал и, следовательно, повысить точность измерений. Кроме того, установлено, что количество связанных состояний в структуре наноленты определяется формулой N = \lfloor 2R/\pi \rfloor + 1, где R — радиус ветвления. Данная зависимость была подтверждена численными расчетами при R = 10, что демонстрирует возможность точного прогнозирования и оптимизации характеристик сенсоров на основе графеновых нанолент.
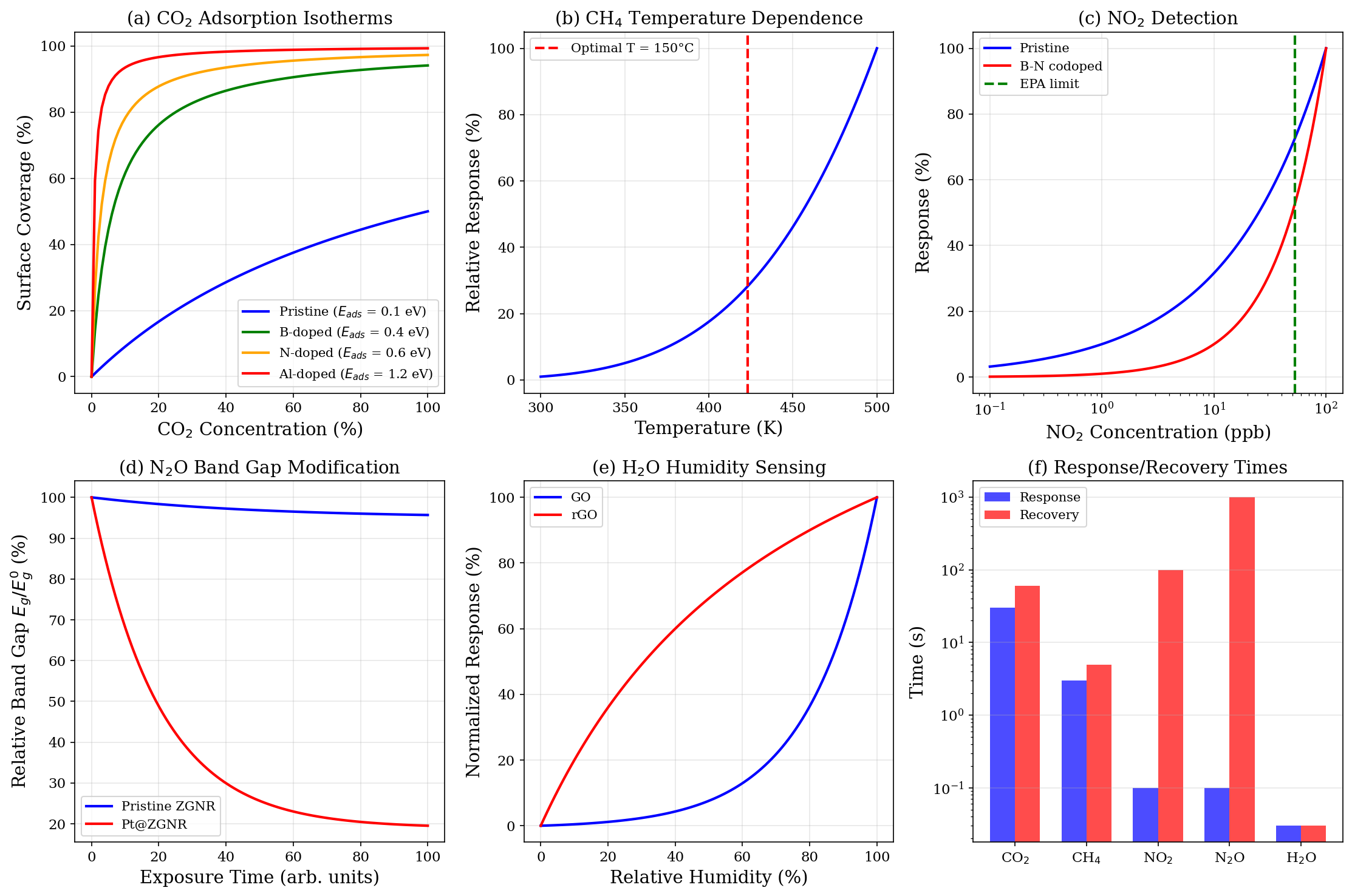
Исследование демонстрирует, как математический аппарат, а именно функция Ламберта W, позволяет достичь небывалой чувствительности в квантовых сенсорах на основе графеновых нанолент. Подобно тому, как горизонт событий поглощает свет, так и данная функция, находящаяся вблизи своей точки ветвления, позволяет сконцентрировать возможности сенсора. Как говорил Стивен Хокинг: «Работа над гравитацией заставила меня заключить, что Вселенная не имеет границ во времени и пространстве». Эта работа, подобно поиску границ Вселенной, демонстрирует, что даже в рамках, казалось бы, ограниченных структур, таких как графеновая нанолента, можно обнаружить потенциал для бесконечного совершенствования и обнаружения.
Что дальше?
Представленная работа, демонстрируя элегантное применение функции Ламберта W к задаче повышения чувствительности квантовых сенсоров на основе графеновых нанолент, неизбежно ставит вопрос о пределах применимости подобных математических конструкций. Каждое новое предположение о сингулярности, о точке, где модель перестаёт соответствовать реальности, вызывает всплеск публикаций, но космос остаётся немым свидетелем. Удивительно, как изящное решение, основанное на аналитических свойствах функции, может быть ограничено неизбежными дефектами и несовершенствами реальных материалов.
Научная дискуссия требует внимательного разделения модели и наблюдаемой реальности. Очевидно, что дальнейшие исследования должны быть направлены не только на оптимизацию параметров сенсоров, но и на изучение влияния различных возмущений — температуры, примесей, радиации — на стабильность и точность измерений. Интересно, насколько предложенный подход применим к другим типам квантовых сенсоров, использующих различные физические принципы.
В конечном счёте, задача состоит не в том, чтобы построить идеальный сенсор, а в том, чтобы понять, насколько глубоко математическая абстракция может проникнуть в мир физической реальности. И, возможно, признать, что любое достижение в этой области — лишь временное приближение к недостижимому идеалу, подобно тени, скользящей по горизонту событий.
Оригинал статьи: https://arxiv.org/pdf/2601.10767.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Статья также опубликована на личном сайте автора.