Квантовые технологии
Кратчайший путь: Квантовый алгоритм для решения задачи коммивояжера
Автор: Денис Аветисян
Исследователи представили новый подход к решению классической задачи оптимизации, используя вариационные квантовые алгоритмы и демонстрируя перспективные результаты для сетей до двенадцати городов.
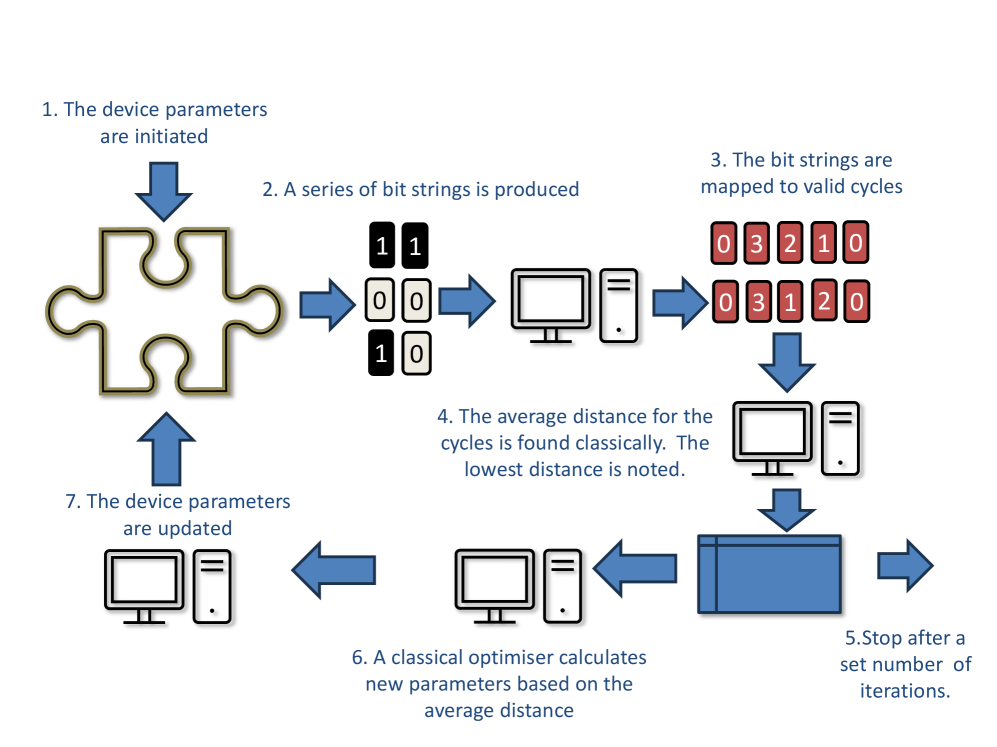
В статье рассматривается применение вариационных квантовых алгоритмов (VQAs) к задаче коммивояжера с использованием QUBO-формулировки и модели квантовой схемы.
Задача коммивояжера, известная своей вычислительной сложностью, долгое время оставалась серьезным вызовом для классических алгоритмов, особенно при увеличении числа городов. В работе «Solving larger Travelling Salesman Problem networks with a penalty-free Variational Quantum Algorithm» представлен новый подход к решению этой NP-трудной задачи, использующий вариационные квантовые алгоритмы (VQA) без штрафных функций. Авторы демонстрируют получение высококачественных решений для сетей до двенадцати городов в шумовых и безшумных симуляциях Qiskit, что является первым успешным моделированием VQA для задачи коммивояжера с таким количеством городов. Сможет ли предложенный метод масштабироваться для решения еще более крупных задач и приблизить нас к квантовому преимуществу в области комбинаторной оптимизации?
За гранью очевидного: постановка задачи коммивояжёра
Проблема коммивояжера, являясь краеугольным камнем комбинаторной оптимизации, на первый взгляд кажется удивительно простой: необходимо найти кратчайший маршрут, проходящий через заданный набор городов и возвращающийся в исходную точку. Однако, эта кажущаяся легкость обманчива. По мере увеличения числа городов, количество возможных маршрутов растет экспоненциально, что делает полный перебор вариантов практически невозможным даже для умеренно больших задач. Вычислительная сложность этой задачи, известная как NP-трудность, означает, что не существует известного алгоритма, способного найти оптимальное решение за полиномиальное время. Таким образом, проблема коммивояжера служит важным эталоном для оценки эффективности алгоритмов и методов приближенного решения сложных оптимизационных задач, оставаясь актуальной и востребованной в различных областях, от логистики и транспорта до генетики и микроэлектроники.
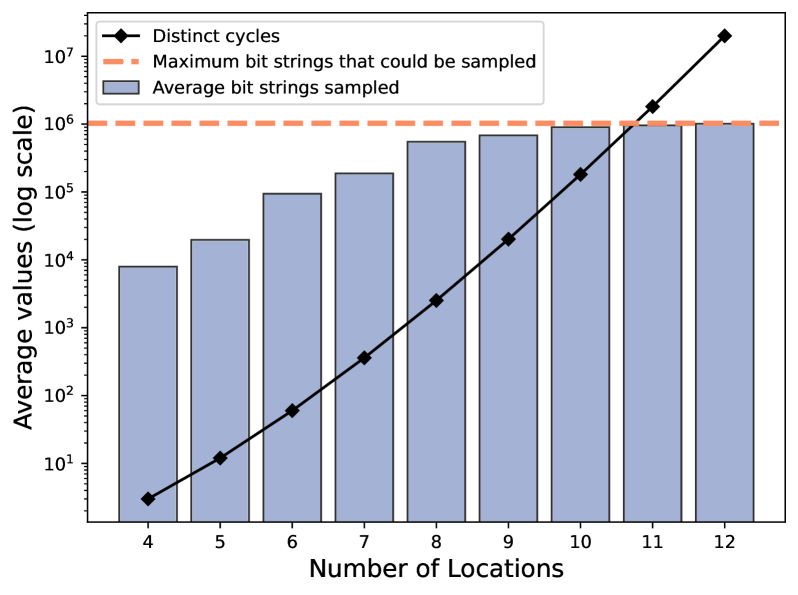
Традиционные методы решения задачи коммивояжера, основанные на полном переборе вариантов, известном как факториальная формулировка, сталкиваются с непреодолимыми трудностями по мере увеличения числа городов. Суть проблемы заключается в том, что количество возможных маршрутов растет экспоненциально — с каждым добавленным городом число вариантов умножается. Например, для десяти городов необходимо рассмотреть различных маршрутов. Для более крупных задач, например, с сотней городов, число возможных маршрутов становится астрономическим и превышает возможности даже самых мощных современных компьютеров. Таким образом, факториальная формулировка, хоть и проста для понимания, быстро становится непрактичной из-за своей вычислительной сложности и неспособности масштабироваться для решения реальных задач.
Несмотря на разработку альтернативных методов решения задачи коммивояжера, не основанных на прямом переборе всех возможных маршрутов (), проблема сохранения вычислительной эффективности при увеличении числа городов остается актуальной. Эти методы, такие как динамическое программирование или алгоритмы локального поиска, позволяют значительно сократить время вычислений по сравнению с полным перебором, однако их сложность все равно растет экспоненциально или полиномиально высокой степени в зависимости от количества точек. В результате, даже с использованием мощных вычислительных ресурсов, поиск оптимального решения для задач с большим числом городов представляет собой серьезную вычислительную задачу, что стимулирует дальнейшие исследования в области аппроксимационных алгоритмов и эвристик, направленных на получение достаточно хороших решений за приемлемое время.
Квантовый горизонт: новые пути оптимизации
Квантовый отжиг представляет собой аппаратный подход к решению задачи коммивояжера (TSP) посредством сопоставления с энергетическим ландшафтом. В этом методе каждая возможная конфигурация маршрута коммивояжера кодируется как состояние квантовой системы, а стоимость маршрута определяется как энергия этого состояния. Квантовый отжиг использует квантовые флуктуации для поиска состояния с минимальной энергией, соответствующего оптимальному или близкому к оптимальному решению TSP. Этот процесс основан на принципах квантовой механики и позволяет эффективно исследовать пространство решений, избегая застревания в локальных минимумах, что характерно для классических алгоритмов оптимизации.
Квантовая схема, использующая вариационные квантовые алгоритмы (ВКА), представляет собой более гибкий подход к оптимизации по сравнению с квантовым отжигом. ВКА позволяют создавать гибридные классическо-квантовые решения, в которых параметризованные квантовые схемы оптимизируются с помощью классических циклов обратной связи. Это позволяет использовать преимущества как квантовых вычислений для обработки сложных задач, так и классических алгоритмов для управления и анализа результатов. Такой подход особенно полезен для решения задач, которые сложно или невозможно эффективно решить с использованием только классических методов, и открывает возможности для разработки специализированных алгоритмов, адаптированных к конкретным типам оптимизационных проблем.
Вариационные квантовые алгоритмы (VQAs), в частности, Алгоритм квантовой аппроксимации (QAOA), используют параметризованные квантовые схемы, оптимизируемые посредством классических циклов обратной связи. В процессе оптимизации параметры квантовой схемы изменяются классическим компьютером, на основе результатов измерений квантового компьютера, с целью минимизации целевой функции, соответствующей решаемой задаче. Успешное моделирование QAOA продемонстрировало достижение оптимальных или близких к оптимальным решений для задач коммивояжера (TSP) с сетями до двенадцати городов, что свидетельствует о потенциальной применимости данного подхода к решению сложных комбинаторных задач.
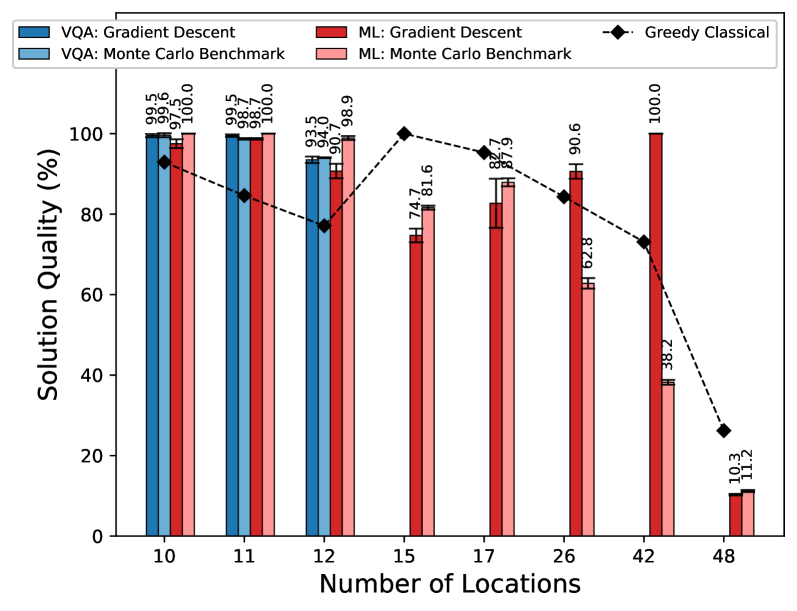
Тонкости оптимизации: поиск оптимальных параметров
Оптимизация параметров в вариационных квантовых алгоритмах (VQA) требует вычисления градиентов функции потерь. Эффективная оценка этих градиентов достигается с помощью методов, таких как правило сдвига параметров (Parameter Shift Rule). Данный метод позволяет аппроксимировать производные функции потерь, смещая параметры цепи и выполняя дополнительные квантовые вычисления. Вместо прямого вычисления производной, что потребовало бы аналитического выражения для функции потерь, правило сдвига параметров использует два дополнительных вычисления цепи с небольшими изменениями параметров, чтобы оценить изменение производительности, что существенно снижает вычислительные затраты и упрощает процесс оптимизации. Данный подход позволяет эффективно оптимизировать параметры VQA, даже для сложных квантовых цепей.
Для повышения эффективности оптимизации параметров вариационных квантовых алгоритмов (VQA) применяются передовые методы, такие как Simultaneous Perturbation Stochastic Approximation (SPSA). SPSA представляет собой стохастический алгоритм, использующий одновременное возмущение всех параметров для оценки градиента функции потерь. Этот подход позволяет снизить дисперсию оценки градиента по сравнению с традиционными методами, такими как метод конечных разностей, что приводит к повышению стабильности и скорости сходимости алгоритма оптимизации. В частности, применение SPSA позволяет эффективно исследовать пространство параметров даже при наличии шума, характерного для квантовых вычислений, и обеспечивает более надежную сходимость к оптимальному решению.
Для оценки и подтверждения эффективности разработанных квантовых алгоритмов проводится сопоставление с классическими моделями машинного обучения. Оценка метрик производится с использованием метода Монте-Карло, обеспечивающего статистическую достоверность результатов. В ходе тестирования, вариационный квантовый алгоритм (VQA) продемонстрировал 100%-ное качество решения для топологий сетей, состоящих до девяти узлов. Данный результат свидетельствует о потенциале квантовых алгоритмов для задач оптимизации в сетях связи и логистики.

Повышение эффективности и представление данных
Методы, такие как “нарезка” (Slicing), позволяют существенно сократить количество необходимых выборок при использовании метода Монте-Карло, что приводит к значительному повышению вычислительной эффективности. Вместо оценки интеграла путем случайного выбора большого числа точек, “нарезка” разбивает область интегрирования на более мелкие, управляемые участки. Это позволяет более точно оценить интеграл на каждом участке, требуя при этом значительно меньше случайных выборок в целом. Эффективность данной техники особенно заметна при решении сложных оптимизационных задач, где традиционные методы Монте-Карло могут требовать огромных вычислительных ресурсов. Применение “нарезки” позволяет добиться существенной экономии времени и ресурсов, делая решение подобных задач более доступным и практичным.
В контексте задачи коммивояжера (TSP), использование серого кодирования представляет собой эффективный метод представления маршрутов, значительно упрощающий математическую формулировку проблемы. Вместо традиционного двоичного кодирования, где смена даже одного бита может привести к одновременному изменению нескольких элементов маршрута, серое кодирование гарантирует, что смена одного бита приводит к изменению только одного ребра в цикле. Это свойство критически важно для алгоритмов оптимизации, таких как метод Монте-Карло, поскольку позволяет выполнять небольшие, локальные изменения в маршруте, что повышает скорость сходимости и снижает вычислительные затраты. Благодаря компактности и эффективности, серое кодирование позволяет более эффективно исследовать пространство решений, что особенно важно для задач TSP с большим числом городов, где количество возможных маршрутов экспоненциально растет с увеличением .
Реализация и моделирование представленных алгоритмов значительно упрощается благодаря использованию открытых программных комплектов для квантовых вычислений, таких как Qiskit. Применение метода SPSA (Simultaneous Perturbation Stochastic Approximation) в сочетании с кэшированием позволило добиться существенного сокращения времени вычислений — с более чем девяти минут до семи секунд. Данный результат демонстрирует не только эффективность предложенных оптимизаций, но и практическую значимость использования современных инструментов разработки для решения сложных задач, связанных с оптимизацией маршрутов и моделированием квантовых систем.
Взгляд в будущее: масштабируемость и новые горизонты
Применение методов «горячего старта» в вариационных квантовых алгоритмах (VQAs) позволяет значительно ускорить процесс оптимизации. Вместо случайного выбора начальных параметров, алгоритм использует предварительно полученные решения, полученные, например, из классических методов или упрощенных моделей. Такой подход, по сути, предоставляет алгоритму «хорошую отправную точку», сокращая число итераций, необходимых для достижения оптимального результата. Исследования показывают, что грамотное использование «горячего старта» может существенно снизить вычислительные затраты и повысить эффективность VQA при решении сложных задач оптимизации, особенно в случаях, когда пространство поиска решений очень велико и неоднородно.
Дальнейшие исследования, направленные на повышение эффективности методов оценки градиента и оптимизационных стратегий, представляются критически важными для масштабирования квантовых алгоритмов решения задач оптимизации. Текущие подходы часто сталкиваются с экспоненциальным ростом вычислительных затрат при увеличении размера задачи, что ограничивает их применимость к реальным, крупномасштабным проблемам. Разработка более точных и ресурсоэффективных методов оценки градиента, таких как стохастические оценки или использование информации о структуре задачи, может существенно снизить эти затраты. Параллельно, исследование новых оптимизационных стратегий, способных эффективно справляться с шумом и неточностями, характерными для квантовых вычислений, является необходимым условием для достижения масштабируемости и практической применимости данных алгоритмов. Оптимизация процессов вычисления градиентов и адаптация алгоритмов к особенностям квантового аппаратного обеспечения позволит решать задачи, недоступные для классических методов.
В конечном итоге, перспективы решения ранее недоступных оптимизационных задач открываются благодаря сближению квантовых алгоритмов, передовых методов представления данных и эффективного программного обеспечения. Доказанное масштабирование числа кубитов, выраженное как , представляет собой значительное преимущество по сравнению с масштабированием , характерным для формулировок QUBO. Это означает, что при увеличении сложности решаемой задачи, требуемое количество кубитов растёт значительно медленнее, что позволяет решать более крупные и сложные проблемы, которые были бы непосильны для классических методов и традиционных квантовых подходов. Такое сочетание факторов создает основу для разработки принципиально новых решений в различных областях, включая логистику, финансы и машинное обучение.
Представленное исследование, стремящееся к решению задачи коммивояжера с использованием вариационных квантовых алгоритмов, напоминает о хрупкости любого теоретического построения. Подобно тому, как горизонт событий поглощает информацию, сложность задачи может быстро выйти за рамцы возможностей классических вычислений. Поль Дирак однажды сказал: «Я считаю, что математическая физика — это единственная истинная наука». Эта фраза особенно актуальна здесь, поскольку поиск оптимальных решений требует не только вычислительной мощности, но и глубокого понимания математических принципов, лежащих в основе самой задачи. Квантовые алгоритмы, предлагаемые в работе, представляют собой попытку расширить границы этого понимания и приблизиться к решению, которое ранее казалось недостижимым. Именно в этом стремлении к неизведанному и заключается истинная красота науки.
Что дальше?
Представленные вычисления, как и любая попытка обуздать сложность задачи коммивояжёра, — лишь приближение к недостижимому идеалу. Каждый найденный маршрут — это не абсолютная истина, а скорее, тень на стене пещеры, указывающая на бесконечность возможных решений. Алгоритмы, основанные на вариационном квантовом подходе, демонстрируют потенциал, но итоговый результат всегда будет ограничен как аппаратными возможностями, так и глубиной нашего понимания лежащих в основе принципов. Утверждения о приближении к «квантовому превосходству» следует воспринимать с осторожностью; каждое новое «достижение» — это лишь более точное приближение, которое завтра может оказаться неверным.
В дальнейшем исследования должны быть направлены не только на увеличение числа решаемых городов, но и на преодоление фундаментальных ограничений, связанных с формулировкой задачи в виде QUBO. Истинным прорывом станет не просто ускорение вычислений, а разработка принципиально новых подходов, позволяющих взглянуть на задачу коммивояжёра под другим углом. Возможно, ключ к решению лежит не в совершенствовании алгоритмов, а в переосмыслении самой постановки вопроса.
В конечном счёте, попытка решить задачу коммивояжёра — это метафора нашего стремления к познанию. Каждый расчёт — это попытка удержать свет в ладони, а он ускользает. И в этом, пожалуй, и заключается истинная красота науки — в бесконечном поиске, а не в достижении окончательного ответа.
Оригинал статьи: https://arxiv.org/pdf/2512.06523.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Статья также опубликована на личном сайте автора.