Квантовая химия: моделирование сложных молекул на пороге реальности

---

Новый гибридный квантово-классический подход открывает путь к точным расчетам свойств лиганд-подобных молекул с использованием доступного квантового оборудования.

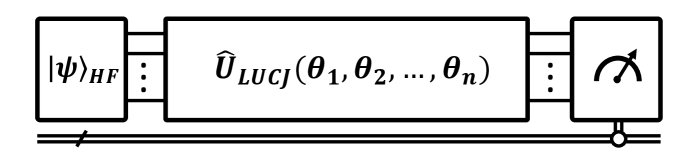
Исследователи объединили теорию вложенных плотностей (DMET) с выборочной квантовой диагонализацией (SQD) для достижения химической точности в моделировании на NISQ-устройствах.

Несмотря на значительный прогресс в вычислительной химии, точное моделирование электронных корреляций в сложных молекулярных системах остается сложной задачей. В данной работе, посвященной ‘Quantum Simulation of Ligand-like Molecules through Sample-based Quantum Diagonalization in Density Matrix Embedding Framework’, предложен гибридный квантово-классический подход, сочетающий теорию вложения матрицы плотности (DMET) и квантовую диагонализацию на основе выборки (SQD). Достигнута химическая точность при моделировании энергии основных состояний лигандоподобных молекул на квантовом оборудовании IBM Eagle R3. Открывает ли это новые перспективы для применения квантовых вычислений в разработке лекарств и моделировании сложных химических процессов?

---

Пределы Классической Квантовой Химии

Традиционные методы квантовой химии, такие как полный метод включения взаимодействий (Full Configuration Interaction, FCI), обеспечивают высокую точность расчетов электронных структур молекул. Однако, их вычислительная стоимость возрастает экспоненциально с увеличением числа электронов и атомных орбиталей в рассматриваемой системе. Это означает, что даже для умеренно сложных молекул, состоящих из нескольких десятков атомов, проведение точных расчетов с использованием FCI становится практически невозможным из-за астрономических требований к вычислительным ресурсам и времени. Таким образом, несмотря на теоретическую привлекательность, экспоненциальное масштабирование ограничивает применимость FCI для моделирования реальных химических систем и стимулирует поиск альтернативных, более эффективных вычислительных подходов, способных преодолеть это фундаментальное ограничение.

Методы приближенного решения уравнения Шрёдингера, такие как теория Хартри-Фока, значительно снижают вычислительные затраты при моделировании молекулярных систем. Однако, упрощая задачу, они неизбежно вносят погрешности в расчеты электронной структуры. В частности, пренебрежение электронной корреляцией, возникающей из-за мгновенного взаимодействия электронов, приводит к завышенным значениям энергии и неточным предсказаниям химических свойств. Это особенно заметно при изучении систем с сильными электронными взаимодействиями, таких как переходные металлы или радикалы, где точность предсказаний существенно снижается, ограничивая возможности использования этих методов для моделирования сложных химических процессов и разработки новых материалов. В результате, для получения надежных результатов часто требуется использование более сложных и ресурсоемких методов, или же принятие компромисса между точностью и вычислительной эффективностью.

В связи с ограничениями традиционных методов квантовой химии, возникла необходимость в разработке более эффективных подходов к моделированию сложных молекулярных систем. В настоящее время активно исследуются гибридные квантово-классические алгоритмы, которые стремятся объединить сильные стороны обоих вычислительных парадигм. Эти алгоритмы используют квантовые компьютеры для решения наиболее сложных задач, таких как вычисление электронной структуры, в то время как классические компьютеры выполняют менее ресурсоемкие операции. Такой подход позволяет преодолеть экспоненциальный рост вычислительных затрат, характерный для классических методов, и открывает перспективы для моделирования молекул и материалов, недоступных для исследования ранее. Перспективные направления включают вариационный квантовый эйнштейновский алгоритм (VQE) и квантовый фазовый алгоритм (QPE), которые демонстрируют потенциал для точного расчета энергии основного состояния и других важных свойств молекул, что может революционизировать области химии, материаловедения и фармацевтики.

Гибридные Алгоритмы: Слияние Классики и Кванта

Гибридные квантово-классические алгоритмы представляют собой перспективный подход к решению сложных вычислительных задач, сочетающий сильные стороны классических и квантовых вычислений. В этих алгоритмах классические компьютеры используются для задач, таких как предобработка данных, оптимизация параметров и постобработка результатов, в то время как вычислительно сложные операции, например, вычисление квантовых состояний или эволюция во времени, делегируются квантовым процессорам. Такой подход позволяет обойти ограничения существующих квантовых аппаратных средств, используя классические ресурсы для выполнения задач, которые они выполняют более эффективно, и квантовые ресурсы для задач, в которых квантовые компьютеры имеют потенциальное преимущество. Это обеспечивает возможность решения задач, недоступных для классических компьютеров, используя доступные квантовые ресурсы.

Вариационный квантовый решатель уравнений (VQE) представляет собой алгоритм, в котором квантовая схема используется для генерации пробной волновой функции $|\psi ⟩$, зависящей от набора параметров $\theta$. Энергия системы, вычисляемая как $E(\theta )=⟨\psi (\theta )|H|\psi (\theta )⟩$, минимизируется с использованием классического оптимизатора. Этот оптимизатор итеративно изменяет параметры $\theta$ квантовой схемы, стремясь к нахождению минимального значения энергии, которое соответствует основному состоянию системы. Таким образом, VQE сочетает в себе возможности квантового вычисления для подготовки волновой функции и классической оптимизации для поиска оптимальных параметров.

Метод Sample-Based Quantum Diagonalization (Диагонализация на основе квантовых выборок) развивает принципы, заложенные в Variational Quantum Eigensolver (VQE), используя квантовые методы выборки для эффективной оценки диагональных элементов гамильтониана $H$. Вместо полного вычисления спектра гамильтониана, метод генерирует выборки из квантового состояния, подготавливаемого квантовой схемой. Эти выборки используются для оценки средних значений операторов, соответствующих диагональным элементам гамильтониана. Эффективность данного подхода заключается в снижении вычислительной сложности по сравнению с традиционными методами диагонализации, особенно в случаях, когда полное вычисление спектра является непосильной задачей для классических компьютеров. Оценка диагональных элементов позволяет приближенно определить собственные значения гамильтониана и, следовательно, энергию основного состояния системы.

Эффективное Представление Состояний и Методы Симуляции

Точное и компактное представление волновой функции является критически важным для эффективного моделирования квантовых систем. Метод Selected Configuration Interaction (SCI) предоставляет способ сосредоточиться на наиболее значимых электронных конфигурациях, отбрасывая менее важные. В SCI, волновой оператор $\Psi$ представляется в виде линейной комбинации выбранных детерминантов, полученных из полного набора детерминантов. Выбор конфигураций осуществляется на основе определенных критериев, таких как энергия или вклад в волновой оператор, что позволяет значительно уменьшить размер базисного набора и вычислительные затраты, сохраняя при этом достаточную точность расчета.

Локальный унитарный кластерный анзац Ястро (LUCJ) представляет собой параметризованный квантовый схематический анзац, разработанный для эффективного приближения волновой функции основного состояния. В основе LUCJ лежит вдохновение, полученное от теории сцепленных кластеров, позволяющее представить волновой оператор в виде экспоненты кластерного оператора $e^T$. В отличие от полного решения уравнения Шрёдингера, LUCJ использует ограниченное число возбужденных кластеров, что значительно снижает вычислительную сложность. Параметризация унитарными преобразованиями позволяет оптимизировать анзац с использованием вариационных методов, минимизируя энергию системы и приближая волновой функцией к истинному основному состоянию.

Методы итерационного самосогласованного восстановления конфигурации (ISCCR) используются для минимизации влияния шума и несовершенств квантового оборудования на точность вычислений. ISCCR предполагает итеративное применение квантовых схем, предназначенных для восстановления исходной, желаемой конфигурации волновой функции после её искажения из-за ошибок. На каждой итерации оценивается степень отклонения текущего состояния от целевого, и параметры квантовой схемы корректируются для уменьшения этого отклонения. Процесс продолжается до достижения сходимости, то есть до тех пор, пока разница между текущим и целевым состояниями не станет достаточно малой, что позволяет получить более надежные результаты, несмотря на наличие шума и ошибок в квантовой системе. Данные методы особенно важны при реализации квантовых алгоритмов, требующих высокой точности и устойчивости к внешним воздействиям.

Реализация и Перспективы Развития

Продемонстрировано успешное применение метода Sample-Based Quantum Diagonalization (SQD) на квантовом процессоре IBM Eagle R3, что открывает новые перспективы для моделирования сложных химических систем. Этот подход позволяет эффективно вычислять собственные значения больших матриц, представляющих молекулярные гамильтонианы, используя относительно небольшое количество квантовых измерений. Благодаря этому, SQD способен справляться с задачами, которые недоступны для классических вычислительных методов, и приближаться к моделированию реальных химических процессов с высокой точностью. Успешная реализация на платформе IBM Eagle R3 подтверждает практическую применимость SQD и его потенциал для развития кванственной химии и материаловедения, позволяя исследовать системы, ранее недоступные для детального изучения.

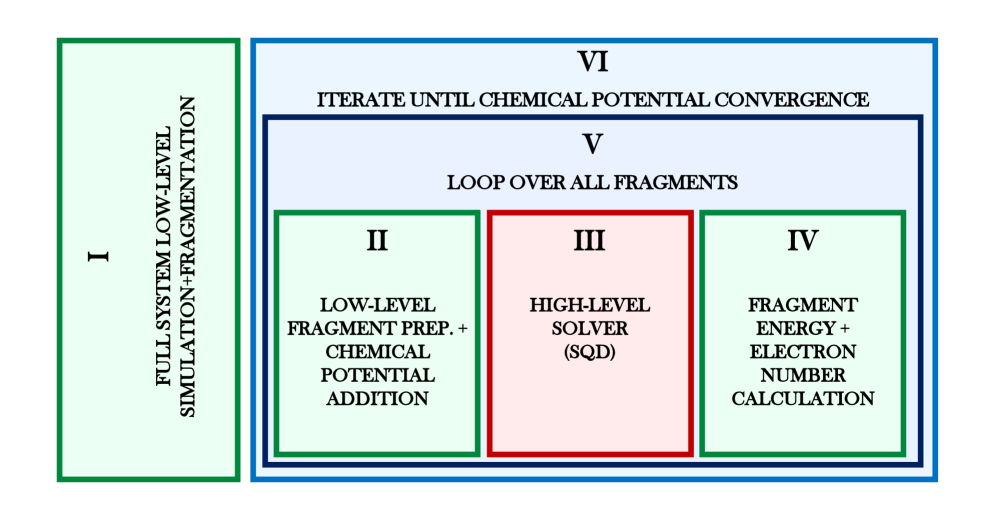
Теория вложения матрицы плотности (DMET) оказалась эффективным инструментом для снижения вычислительных затрат при моделировании сложных квантовых систем. Вместо обработки всей системы целиком, DMET фокусируется на локальном фрагменте, описывая его с высокой точностью, а взаимодействие с остальной системой учитывается посредством вложений. Этот подход позволяет существенно уменьшить размер решаемой задачи, поскольку вычисления проводятся только для активного фрагмента, а не для всей молекулы или материала. В рамках данного исследования, интеграция DMET с алгоритмами квантовой диагонализации позволила успешно моделировать системы с пространством Гильберта размерностью более $10^9$, достигая при этом химической точности в расчете энергий — менее 1 ккал/моль. Такое сочетание методов открывает новые возможности для изучения сложных химических процессов и материалов, которые ранее были недоступны для квантово-химических расчетов.

В ходе исследования удалось достичь результатов, соответствующих химической точности — погрешность составила менее 1 ккал/моль при сравнении с эталонными расчетами, выполненными методом DMET-FCI. Это подтверждает высокую эффективность предложенного подхода к квантовому моделированию. Достижение такой точности, особенно при работе с системами, требующими значительных вычислительных ресурсов, демонстрирует перспективность использования методов квантовой диагонализации на основе выборок для решения сложных задач в химии и материаловедении. Полученные данные указывают на возможность проведения высокоточных расчетов свойств молекул и материалов, что открывает новые горизонты для разработки инновационных технологий и материалов.

Исследования были проведены на системе с размерностью гильбертова пространства, достигающей 1,073,741,824, что демонстрирует впечатляющий масштаб моделируемых квантовых систем. Такая высокая размерность, эквивалентная более чем миллиарду возможных квантовых состояний, ранее была недостижима для прямого моделирования на квантовых компьютерах. Достижение этой отметки указывает на значительный прогресс в области квантовых вычислений и открывает новые возможности для изучения сложных молекулярных систем и материалов, представляющих интерес для химии и физики. Возможность оперировать с системами столь высокого порядка является ключевым шагом на пути к решению реальных задач, которые требуют точного моделирования квантовых эффектов в многочастичных системах.

Достижение максимальной глубины квантовой схемы в 1081 — значимая веха, демонстрирующая возрастающую сложность и потенциал разработанного подхода к квантовой диагонализации. Такая глубина свидетельствует о необходимости преодоления ограничений, связанных с когерентностью кубитов и шумами в современных квантовых процессорах. Разработка и реализация схем с подобной глубиной требует оптимизации как алгоритмов, так и аппаратной реализации, что открывает путь к моделированию более сложных и реалистичных химических систем. Подобные достижения позволяют исследовать квантовые эффекты, недоступные для классических вычислений, и приближают возможность создания квантовых симуляторов для решения актуальных задач в химии и материаловедении. Преодоление барьеров, связанных с глубиной квантовых схем, является ключевым шагом на пути к практическому применению квантовых вычислений.

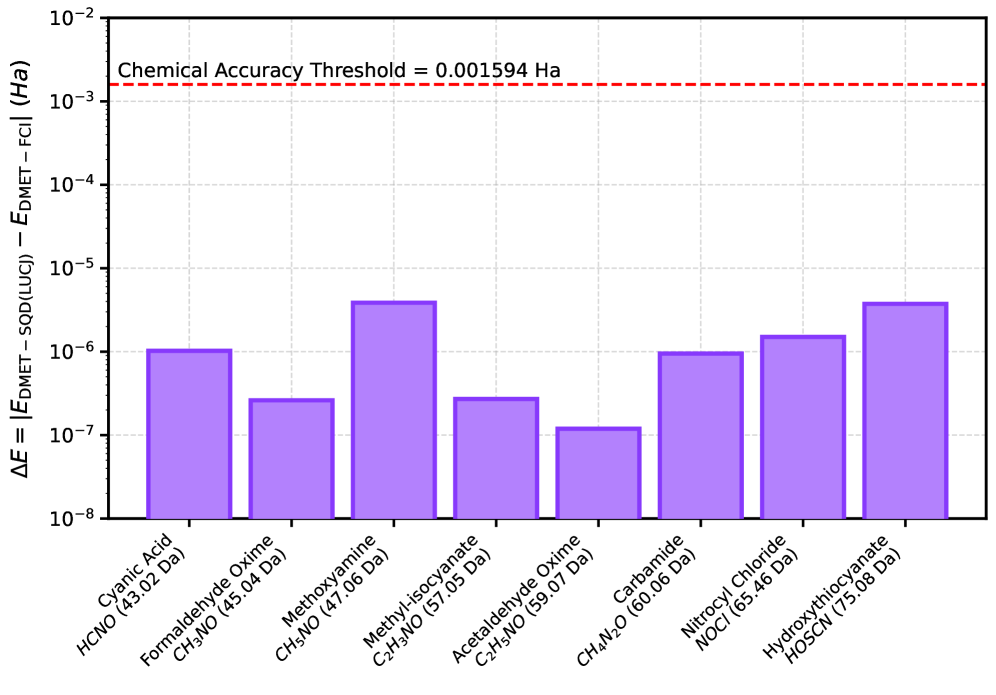
Результаты исследования демонстрируют высокую точность разработанного метода, что подтверждается крайне незначительной разницей в энергии между расчетами, выполненными с использованием Sample-Based Quantum Diagonalization (DMET-SQD), и эталонными значениями, полученными с помощью Full Configuration Interaction (DMET-FCI). Различие в энергии, не превышающее $10^{-5}$ Хартри, свидетельствует о том, что предложенный подход способен с высокой степенью достоверности моделировать сложные квантово-химические системы. Такая согласованность между двумя методами подтверждает перспективность DMET-SQD как эффективного инструмента для проведения точных расчетов в квантовой химии, особенно в случаях, когда использование классических методов становится вычислительно затруднительным.

Исследование демонстрирует, что даже сложные химические симуляции, такие как моделирование лигандов, неизбежно сводятся к приближениям и компромиссам. Гибридный квантово-классический подход, описанный в работе, — лишь ещё один способ уложить непостоянную квантовую реальность в прокрустовы рамки классических алгоритмов. Как справедливо заметил Альберт Эйнштейн: «Самое главное — не переставать задавать вопросы». В данном случае, вопрос о точности симуляции постоянно сталкивается с ограничениями доступного квантового оборудования и необходимостью выбора наиболее адекватного уровня приближения. В конечном итоге, даже самая элегантная архитектура, основанная на DMET и SQD, со временем станет лишь очередным способом обхода проблем, а не их решением.

Что дальше?

Представленная работа, как и многие другие в области квантовых вычислений, демонстрирует возможность решения «интересной» задачи на смоделированном железе. Достижение «химической точности» для лигандоподобных молекул — это, безусловно, прогресс, но нельзя забывать, что каждая новая «революционная» библиотека — это лишь очередная обёртка над старыми багами. Утверждения о применимости на «ближайших» квантовых устройствах звучат оптимистично, однако опыт подсказывает, что реальное железо всегда найдёт способ сломать даже самую элегантную теорию.

Основной вопрос, который остаётся без ответа, — это масштабируемость. Увеличение числа атомов в моделируемой системе неизбежно приведёт к экспоненциальному росту вычислительных затрат, как классических, так и квантовых. Вполне вероятно, что в итоге потребуется ещё один уровень приближений, который сведёт на нет все предыдущие достижения. Помнят ли вообще разработчики, что «всё работало, пока не пришёл agile»?

В конечном счёте, вся эта работа — ещё один шаг в бесконечном цикле оптимизаций и приближений. Иногда кажется, что DevOps — это когда инженеры смирились с тем, что идеального решения не существует. Всё новое — это просто старое с худшей документацией. И, возможно, через десять лет кто-нибудь скажет, что Density Matrix Embedding Theory была просто «интересной идеей».

---

Оригинал статьи: https://arxiv.org/pdf/2511.22158.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/