Квантовая симуляция: Модель Швингера на решетке

---

В статье представлен обзор решеточной формулировки модели Швингера, ее возможностей и перспектив использования в качестве эталона для квантовых симуляторов теорий поля.

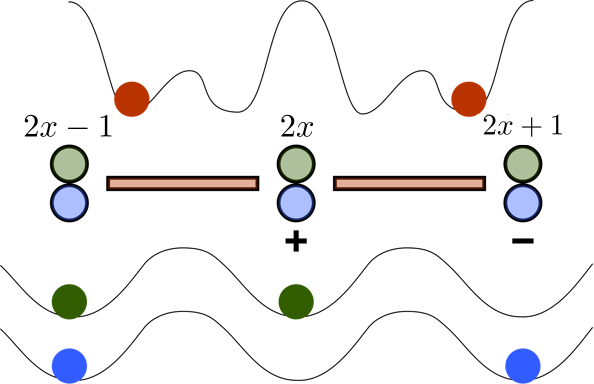
Рассмотрены одномерный и двухмерный случаи, а также различные подходы к реализации и исследованию модели в квантовых системах.

Несмотря на кажущуюся простоту, непертурбативное исследование квантовой электродинамики в сильных полях представляет собой сложную задачу. Данная работа, озаглавленная ‘The Lattice Schwinger Model and Its Quantum Simulation’, посвящена обзору решетковой формулировки модели Швингера, в частности, случаев с одним и двумя ароматами. Показано, как аномалия воспроизводится на решетке и как эта модель может служить эталоном для схем квантового моделирования взаимодействующих теорий поля. Какие перспективы открываются для реализации и изучения этой модели в квантовых системах и для разработки новых алгоритмов квантового моделирования?

---

Фундаментальная модель: Исследование непертурбативных режимов

Модель Швингера, упрощенная версия квантовой электродинамики (КЭД), представляет собой важную платформу для проверки непертурбативных методов из-за присущей ей сложности. В отличие от возмущающих расчетов, хорошо работающих в КЭД при высоких энергиях, модель Швингера демонстрирует явления, такие как спонтанное нарушение хиральной симметрии и образование конденсата, которые требуют подходов, способных учесть сильные взаимодействия. Её упрощенная структура, описывающая взаимодействие безмассовых фермионов с компактифицированным электромагнитным полем, позволяет исследователям сосредоточиться на фундаментальных аспектах непертурбативной физики, избегая при этом вычислительных трудностей, связанных с более реалистичными моделями. Таким образом, модель Швингера служит своеобразным полигоном для разработки и тестирования алгоритмов, предназначенных для решения сложных задач в квантовой теории поля, особенно в областях, где традиционные методы оказываются неэффективными.

Традиционные вычислительные методы, применяемые для моделирования динамики Швингера, сталкиваются со значительными трудностями, особенно при описании явления спонтанного нарушения хиральной симметрии. Эта проблема возникает из-за того, что стандартные подходы, основанные на теории возмущений, оказываются неэффективными в сильных полях, характерных для данной модели. Спонтанное нарушение хиральной симметрии проявляется в возникновении ненулевого вакуумного ожидания оператора $\bar{\psi }\psi$, что требует учета непертурбативных эффектов. Неспособность адекватно описать этот процесс приводит к неточным результатам и затрудняет понимание фундаментальных аспектов квантовой электродинамики в сильных полях, что подчеркивает необходимость разработки более совершенных вычислительных стратегий и латтисных формулировок.

Неспособность традиционных методов адекватно моделировать динамику модели Швингера, в особенности такие явления, как спонтанное нарушение хиральной симметрии, служит мощным стимулом для разработки передовых решётчатых формулировок и методов симуляции. Исследователи активно работают над усовершенствованием алгоритмов, стремясь создать более точные и эффективные инструменты для изучения непертурбативных аспектов квантовой электродинамики. Это включает в себя разработку новых решётчатых действий, оптимизацию алгоритмов Монте-Карло и использование высокопроизводительных вычислительных ресурсов для решения сложных задач, связанных с сильными взаимодействиями и нетривиальной топологией вакуума. Успехи в этой области позволят глубже понять фундаментальные свойства материи и открыть новые горизонты в физике элементарных частиц, а также способствуют развитию вычислительной физики и информационных технологий.

Дискретизация пространства-времени: Решётка как инструмент

Модель Швингера на решетке предоставляет важную основу для численных исследований модели Швингера, позволяя исследовать непертурбативные режимы. В то время как аналитическое решение модели Швингера ограничено пертурбативными вычислениями, дискретизация пространства-времени посредством решетки позволяет применять численные методы для изучения явлений, таких как спонтанное нарушение симметрии и образование пар частиц-античастиц. Эта дискретизация, хотя и вводит определенные артефакты, позволяет напрямую рассчитывать корреляционные функции и другие физические величины, которые недоступны в пертурбативной теории. В частности, решетные вычисления позволяют исследовать динамику вакуума и структуру адронов, что является ключевым для понимания непертурбативной квантовой электродинамики ($QED$).

Дискретизация, осуществляемая, например, с помощью фермионов со стэгерной формой, вносит определенные сложности в анализ модели Швингера на решетке. В частности, использование стэгерных фермионов приводит к нарушению хиральной симметрии, что влияет на спектр частиц и требует особого внимания при интерпретации результатов численного моделирования. Кроме того, дискретизация может приводить к появлению нежелательных артефактов, таких как ложные полюса или искажение дисперсионного соотношения, которые необходимо учитывать при анализе и экстраполяции данных. Конкретно, при дискретизации пространства-времени на решетку с шагом $a$, импульс $p$ становится квантованным, а спектр энергии приобретает дискретный характер, что может потребовать использования методов регуляризации и перенормировки для получения физически корректных результатов.

Комбинация Гамильтонова подхода и Решётчатой модели Швингера позволяет проводить прямое численное моделирование динамики в реальном времени. Традиционные методы, основанные на функциональном интеграле, испытывают трудности при исследовании эволюции во времени из-за необходимости аналитического продолжения. Гамильтонов формализм, напротив, оперирует с оператором Гамильтона $H$, позволяя решать уравнение Шредингера $i\hslash \frac{\partial }{\partial t}|\psi (t)⟩=H|\psi (t)⟩$ численно. Решётчатая формулировка обеспечивает дискретизацию пространства-времени, что делает возможным проведение численных расчетов на конечных ресурсах. Такой подход особенно важен для изучения непертурбативных явлений, таких как рождение пар, и динамики сильных полей, где стандартные методы оказываются неэффективными.

За пределами стандартной дискретизации: Квантовая связь как новый взгляд

Модель квантовых связей (Quantum Link Model) является расширением модели Швингера на решетке, в которой калибровочные поля представляются как квантовые операторы, а не классические переменные. Это отличие позволяет исследовать непертурбативные аспекты динамики, которые недоступны в стандартных подходах, основанных на разложении в ряд возмущений. В то время как в модели Швингера на решетке калибровочные поля задаются как параметры, в модели квантовых связей каждый линк решетки описывается оператором, действующим в гильбертовом пространстве. Такое представление позволяет учесть квантовые флуктуации калибровочных полей и, следовательно, более точно моделировать явления, связанные с непертурбативными эффектами, такие как конфайнмент и динамическое зарождение пар.

Реализация калибровочной симметрии в квантовых симуляциях требует применения специализированных методов, таких как метод энергетического штрафа (Energy Penalty). Данный подход позволяет обеспечить выполнение локальной калибровочной инвариантности, вводя в гамильтониан штрафные члены, пропорциональные нарушению условий калибровочной инвариантности. Эти штрафные члены подавляют конфигурации, не удовлетворяющие условиям калибровочной симметрии, эффективно проецируя систему в подпространство, где симметрия сохраняется. Эффективность метода зависит от выбора коэффициента штрафа, который должен быть достаточно большим для обеспечения соблюдения симметрии, но при этом не слишком большим, чтобы не подавить физические процессы, которые необходимо моделировать. Альтернативные методы включают использование вспомогательных полей и другие техники, направленные на явное обеспечение калибровочной инвариантности в рамках численных расчетов.

Расширение по малой константе связи, известное как разложение по сильному взаимодействию (Strong Coupling Expansion), предоставляет ценные данные о поведении Квантовой Модели Связей ($Quantum$ $Link$ $Model$) в определенных режимах. Этот подход позволяет аналитически и численно исследовать систему, когда взаимодействие между частицами достаточно велико, что затрудняет применение стандартных методов теории возмущений. В частности, разложение по сильному взаимодействию используется для вычисления корреляционных функций, определения фазовых диаграмм и изучения конфайнмента кварков. Хотя метод и имеет ограничения в применимости при уменьшении константы связи, он обеспечивает важную отправную точку для более сложных численных симуляций и аналитических исследований, особенно в областях, где непертурбативные эффекты преобладают.

Квантовое моделирование и экспериментальная проверка: От теории к практике

Переход от простой модели Швингера к двух-ароматной версии значительно повышает её применимость к реальным физическим системам. Изначальная модель, описывающая квантовую электродинамику в одном пространственном измерении, является упрощением, позволяющим исследовать фундаментальные аспекты, такие как спонтанное нарушение симметрии и образование пар частиц-античастиц. Однако, расширение до двух ароматов, фактически введение двух типов частиц, приближает модель к описанию физики кварков и глюонов в квантовой хромодинамике. Это позволяет исследовать более сложные явления, такие как смешивание частиц и динамическое нарушение симметрии, которые играют ключевую роль в понимании структуры адронов и поведения сильных взаимодействий. Такое расширение требует более сложных вычислений и большей вычислительной мощности, но взамен предоставляет более реалистичную и информативную картину физических процессов, происходящих в мире элементарных частиц. Изучение двух-ароматной модели Швингера открывает новые возможности для проверки теоретических предсказаний и углубления понимания фундаментальных законов природы.

Квантовое моделирование спина-1/2 предоставляет мощную платформу для реализации решёточных формулировок, обеспечивая контролируемую среду для изучения сложных физических систем. В отличие от классических вычислений, квантовые системы позволяют напрямую моделировать квантовые явления, такие как динамика элементарных частиц и взаимодействие между ними. Решёточные модели, такие как двухвкусная модель Швингера, требуют огромных вычислительных ресурсов при классическом моделировании, но квантовое моделирование с использованием, например, оптических решёток для удержания и манипулирования атомами, предлагает альтернативный подход. Этот метод позволяет эффективно исследовать непертурбативные аспекты квантовой теории поля, а также проверять предсказания теоретических моделей в контролируемых лабораторных условиях, что открывает новые возможности для понимания фундаментальных законов природы и разработки новых материалов с уникальными свойствами. Точность и масштабируемость таких квантовых симуляторов являются ключевыми факторами для дальнейшего развития этой области исследований.

В основе современных квантовых симуляций лежит использование оптических решеток — структур, создаваемых пересекающимися лазерными лучами, которые формируют потенциальные ямы для удержания и манипулирования отдельными атомами. Эти решетки, по сути, выступают в роли искусственных кристаллов, позволяя исследователям точно контролировать взаимодействие между атомами и эмулировать поведение сложных квантовых систем, таких как модели Швингера. Благодаря прецизионному управлению параметрами лазера, можно изменять глубину потенциальных ям, расстояние между атомами и даже геометрию решетки, создавая настраиваемую платформу для изучения фундаментальных вопросов квантовой физики и моделирования материалов с экзотическими свойствами. Такой подход позволяет исследовать явления, недоступные для классического моделирования, и открывает новые возможности для разработки квантовых технологий.

Исследование решетчатой модели Швингера, представленное в данной работе, демонстрирует, как сложные явления, такие как спонтанное нарушение хиральной симметрии, могут возникать из локальных взаимодействий. Наблюдаемая структура, формирующаяся в сильном взаимодействии, не требует централизованного проектирования, а скорее возникает как следствие базовых правил, определяющих взаимодействие квантовых полей. В этом контексте, замечание Джона Белла: «Порядок не нуждается в архитекторе — он возникает из локальных правил» — находит глубокий отклик, подчеркивая, что устойчивость системы обусловлена не внешним контролем, а самоорганизацией, возникающей из малых взаимодействий, способных привести к значительным изменениям в поведении квантовой системы.

Что впереди?

Рассмотренная здесь решетчатая версия модели Швингера, как и любая попытка свести сложность к дискретным взаимодействиям, лишь подчеркивает фундаментальную истину: порядок не нуждается в архитекторе. Спонтанное нарушение хиральной симметрии, являющееся ключевым аспектом этой модели, не возникает из-за внешнего контроля, а проявляется как следствие локальных правил, заданных решеткой. Искать «управление» этой симметрией — иллюзия; влияние на параметры взаимодействия — единственно реальный путь.

Очевидно, что дальнейшее развитие квантового моделирования этих систем потребует не столько усовершенствования алгоритмов, сколько переосмысления самой цели. Не стоит стремиться к «точному» воспроизведению поля, а следует сосредоточиться на изучении emergent свойств, возникающих из взаимодействия квантовых элементов. Иногда, как ни парадоксально, пассивность — лучший инструмент: позволить системе эволюционировать, а затем внимательно наблюдать за ее самоорганизацией.

Более того, упор на сильное взаимодействие, характерный для данной модели, наталкивает на мысль о необходимости пересмотра концепции «малых возмущений», столь привычной в теоретической физике. Порядок проявляется не вблизи точек равновесия, а в хаосе, где локальные правила определяют глобальную структуру. Возможно, именно в изучении этих непертурбативных режимов кроется ключ к пониманию более сложных явлений в физике высоких энергий.

---

Оригинал статьи: https://arxiv.org/pdf/2512.11533.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/