Квантовая термодинамика: моделирование за пределами возможностей классических вычислений

---

Новый квантовый алгоритм позволяет эффективно моделировать термодинамические процессы в квантовых системах при конечных температурах, открывая перспективы для изучения сложных физических явлений.

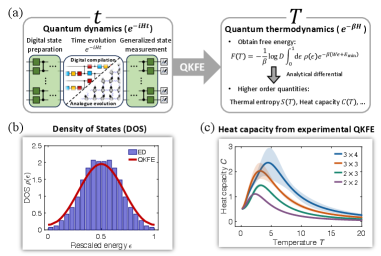
В статье представлен алгоритм QKFE и продемонстрирована его реализация на сверхпроводящих квантовых процессорах для моделирования квантовой термодинамики с использованием методов расширения квантовой функции ядра.

Характеризация квантовых фаз материи при конечных температурах представляет собой сложную задачу для классических вычислений. В работе «Алгоритмическое квантовое моделирование квантовой термодинамики» предложен новый алгоритм, QKFE, и продемонстрирована его реализация на сверхпроводящих кубитах для эффективного моделирования квантовой термодинамики при конечных температурах. Полученные результаты демонстрируют количественное соответствие с точными вычислениями, открывая путь к изучению термодинамических свойств материалов и разработке новых лекарственных препаратов. Возможно ли создание универсальной платформы для квантового моделирования термодинамических потенциалов и какие новые горизонты она откроет для материаловедения и химии?

---

Пределы Классических Вычислений: Вызов для Новых Подходов

Традиционные вычислительные методы, такие как метод Монте-Карло и тензорные сети, сталкиваются с существенными трудностями при моделировании систем, характеризующихся сильной квантовой запутанностью и так называемой “проблемой знака”. Метод Монте-Карло, полагающийся на случайные выборки, испытывает экспоненциальный рост вычислительных затрат по мере увеличения запутанности, поскольку необходимо усреднять все возможные конфигурации системы. Тензорные сети, хоть и эффективны для систем с ограниченной запутанностью, быстро становятся неуправляемыми при её усилении, требуя экспоненциального увеличения вычислительных ресурсов и памяти. “Проблема знака”, возникающая в квантовых вычислениях, связана с осциллирующими вкладами в интегралы, что приводит к статистическим флуктуациям и затрудняет получение достоверных результатов, особенно в системах с фермионами. Эти ограничения существенно препятствуют прогрессу в материаловедении и физике высоких энергий, где точные симуляции необходимы для понимания и предсказания свойств сложных квантовых систем.

Ограничения классических вычислений особенно остро ощущаются в материаловедении и физике высоких энергий, где точные моделирования являются основой для прогресса. Например, при разработке новых материалов с заданными свойствами, необходимо понимать взаимодействие множества электронов — задача, требующая экспоненциального роста вычислительных ресурсов с увеличением числа частиц. Аналогично, в физике высоких энергий, моделирование столкновений частиц и изучение свойств элементарных частиц сталкивается с теми же трудностями, что препятствует пониманию фундаментальных законов Вселенной. Невозможность адекватно симулировать сложные квантовые системы с помощью классических методов замедляет открытие новых материалов, лекарств и углубление знаний о природе реальности, подчеркивая необходимость поиска альтернативных подходов к вычислениям.

Ограничения классических вычислений, проявляющиеся в неспособности эффективно моделировать системы с сильной квантовой запутанностью и сталкивающиеся с так называемой “проблемой знака”, требуют принципиального пересмотра подходов к вычислительным задачам. Традиционные методы, такие как метод Монте-Карло и тензорные сети, оказываются недостаточно эффективными при исследовании сложных квантовых явлений. Это особенно критично для таких областей науки, как материаловедение и физика высоких энергий, где точные численные симуляции являются ключевым инструментом для прогресса. В связи с этим, возникает необходимость в разработке и внедрении вычислительных парадигм, способных непосредственно оперировать с квантовыми состояниями и эффективно решать задачи, недоступные для классических компьютеров, что открывает путь к пониманию и использованию возможностей квантового мира.

Квантовые Вычисления: Новый Горизонт в Вычислительной Модели

Квантовые вычисления представляют собой принципиально новый подход к обработке информации, основанный на использовании принципов суперпозиции и запутанности. В отличие от классических компьютеров, оперирующих битами, принимающими значения 0 или 1, квантовые компьютеры используют кубиты. Кубит может находиться в состоянии суперпозиции, представляя собой комбинацию состояний 0 и 1 одновременно. Запутанность позволяет установить корреляцию между двумя или более кубитами, так что изменение состояния одного мгновенно влияет на состояние другого, независимо от расстояния между ними. Эти свойства позволяют квантовым алгоритмам исследовать гораздо большее количество возможных решений одновременно, что потенциально позволяет решать задачи, невыполнимые для классических компьютеров, например, факторизацию больших чисел или моделирование сложных молекулярных систем.

Цифровое квантовое моделирование реализует квантовые алгоритмы посредством дискретных квантовых вентилей и схем, что позволяет моделировать сложные системы, недоступные для классических вычислений. В основе метода лежит представление квантовых состояний и операций над ними в дискретной форме, используя такие вентили как $X$, $Y$, $Z$, $H$ и $CNOT$. Квантовые схемы, состоящие из последовательности этих вентилей, применяются к кубитам для выполнения требуемых вычислений. Этот подход позволяет исследовать поведение молекул, материалов и других сложных систем, моделируя их квантово-механические свойства с высокой точностью, что открывает возможности для разработки новых лекарств, материалов и технологий.

Успех квантовых вычислений напрямую зависит от преодоления проблем, связанных с декогеренцией и точностью работы квантовых вентилей. Декогеренция, потеря квантовой информации из-за взаимодействия с окружающей средой, ограничивает время, в течение которого можно выполнять вычисления. Современные сверхпроводящие квантовые процессоры демонстрируют значительные улучшения в точности работы отдельных кубитов, достигая значений в 99.9%, и двухкубитных вентилей CZ (Controlled-Z) — 99.6%. Повышение этих показателей, в частности, за счет улучшения изоляции кубитов и оптимизации управляющих импульсов, является критически важным для масштабирования квантовых систем и выполнения сложных вычислений.

Продвинутые Техники Квантового Моделирования: Эффективность и Точность

Протокол виртуальной копии упрощает вычисления, используя виртуальную копию квантовой системы, что становится возможным благодаря антикоммутативной симметрии. Этот подход позволяет эффективно моделировать сложные квантовые системы, уменьшая вычислительную сложность за счет манипулирования свойствами антикоммутаторов операторов. В частности, использование антикоммутативной симметрии позволяет разделить задачу на более управляемые подзадачи, снижая требования к вычислительным ресурсам и памяти. Реализация протокола позволяет значительно ускорить вычисления без потери точности, что особенно важно при моделировании систем с большим количеством частиц или сложных взаимодействий.

Протокол опорного состояния (Reference-State Protocol) обеспечивает эффективное извлечение термодинамических свойств квантовой системы, используя симметрию фазы U(1). Этот подход позволяет выразить гамильтониан системы в терминах операторов, коммутирующих с $U(1)$, что упрощает вычисление термодинамических величин, таких как энергия, энтропия и теплоемкость. Использование симметрии фазы позволяет существенно снизить вычислительную сложность по сравнению с традиционными методами, особенно при моделировании систем с большим числом частиц, и позволяет эффективно анализировать термодинамические свойства при различных температурах и давлениях.

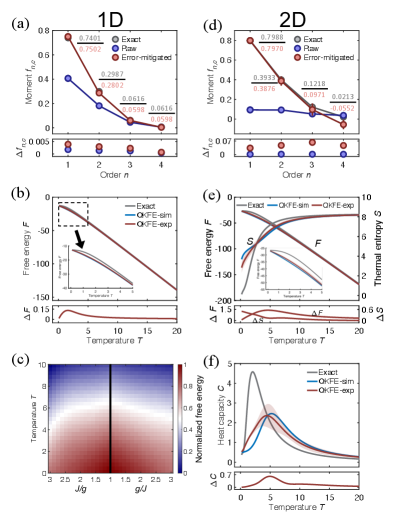
Реализация протоколов виртуальных копий и опорных состояний на современных квантовых процессорах продемонстрировала возможность проведения сложных симуляций. Достигнуто количественное согласие с точными результатами расчетов, при этом расхождения в разложениях в ряд Тейлора (expansion moments) снижены до значений менее $10^{-2}$. Это свидетельствует о практической применимости данных методов для моделирования квантовых систем, ранее недоступных для численного анализа из-за вычислительных ограничений.

Повышение Точности с Помощью Смягчения Ошибок: Путь к Надежным Результатам

Методы смягчения ошибок, известные как Gem Error Mitigation, играют ключевую роль в преодолении влияния шумов и несовершенств, свойственных современному квантовому оборудованию. Эти техники, по сути, представляют собой алгоритмические процедуры, направленные на уменьшение вероятности получения неверных результатов из-за ошибок, возникающих в процессе квантовых вычислений. В отличие от квантовой коррекции ошибок, требующей значительных аппаратных ресурсов, Gem Error Mitigation оперирует с данными, полученными в результате вычислений, и позволяет оценить истинное значение результата, минимизируя влияние шума. Применение этих методов особенно важно для получения достоверных результатов при моделировании сложных систем, где даже незначительные погрешности могут существенно исказить конечный результат и привести к неверным выводам.

Сочетание передовых протоколов моделирования с методами смягчения ошибок позволило исследователям добиться значительно большей точности результатов, что подтверждается измерениями теплоемкости. В ходе экспериментов, отклонения полученных данных от точных значений составили менее $10^{-2}$. Такой уровень прецизионности открывает новые горизонты для моделирования сложных материалов и явлений, позволяя изучать их свойства с беспрецедентной детализацией и ускоряя тем самым процесс научных открытий в различных областях физики и химии.

Повышенная точность квантовых симуляций, достигнутая благодаря методам смягчения ошибок, открывает принципиально новые горизонты для исследования сложных материалов и явлений. Теперь возможно моделирование систем, которые ранее были недоступны из-за накопившихся погрешностей и шумов в квантовом оборудовании. Это касается, в частности, изучения высокотемпературных сверхпроводников, катализаторов и даже процессов, происходящих в биологических системах на молекулярном уровне. Ученые получают возможность проверять теоретические предсказания с беспрецедентной детализацией, что значительно ускоряет процесс научного открытия и позволяет разрабатывать новые материалы с заданными свойствами. Возможность точного моделирования сложных квантовых систем стимулирует развитие новых технологий в различных областях, от материаловедения до фармацевтики и энергетики, открывая путь к инновациям и прорывам в науке и технике.

Представленное исследование демонстрирует изящную гармонию между теоретическими построениями и практическими реализациями в области квантовой термодинамики. Алгоритм QKFE, детально описанный в работе, позволяет преодолеть ограничения классических методов моделирования, эффективно симулируя системы при конечных температурах. Это достижение особенно ценно, поскольку открывает новые возможности для изучения сложных квантовых явлений. Как однажды заметил Макс Планк: «Наука не является собранием фактов, а методом организации фактов». Именно этот принцип лежит в основе представленной работы — стремление к систематизации и эффективной организации информации о квантовых системах для достижения более глубокого понимания их поведения.

Куда Ведет Этот Путь?

Представленный подход, хотя и демонстрирует значительный прогресс в моделировании квантовой термодинамики, всё же оставляет вопросы. Элегантность алгоритма QKFE, несомненно, радует глаз, однако истинное испытание заключается в масштабируемости. Реальные физические системы редко бывают идеально симметричными, и хотя работа затрагивает вопросы смягчения ошибок, влияние несовершенства оборудования остаётся существенной проблемой. Необходимо более глубокое исследование влияния различных функций ядра на точность и эффективность симуляций.

Следующим шагом представляется не просто увеличение количества кубитов, а разработка более изящных методов кодирования информации. Поиск алгоритмов, которые могут эффективно использовать ограниченные ресурсы квантового оборудования, становится первостепенной задачей. Важно понимать, что квантовые вычисления — это не замена классическим, а их дополнение. Поэтому, гармоничное сочетание классических и квантовых методов, вероятно, окажется наиболее плодотворным путем.

В конечном счете, ценность любого алгоритма определяется не его сложностью, а его способностью пролить свет на фундаментальные вопросы. Квантовая термодинамика, как область, полна парадоксов и противоречий. Алгоритмы, подобные QKFE, могут стать инструментом для разрешения этих противоречий, но лишь в том случае, если они будут развиваться не только в направлении повышения производительности, но и в направлении углубления понимания лежащих в основе физических принципов.

---

Оригинал статьи: https://arxiv.org/pdf/2511.22898.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/