Квантово-классический тандем: новый подход к решению задач электромагнитного рассеяния

---

Исследователи предлагают гибридный алгоритм, объединяющий возможности квантовых и классических вычислений для повышения эффективности решения уравнений электромагнитного поля.

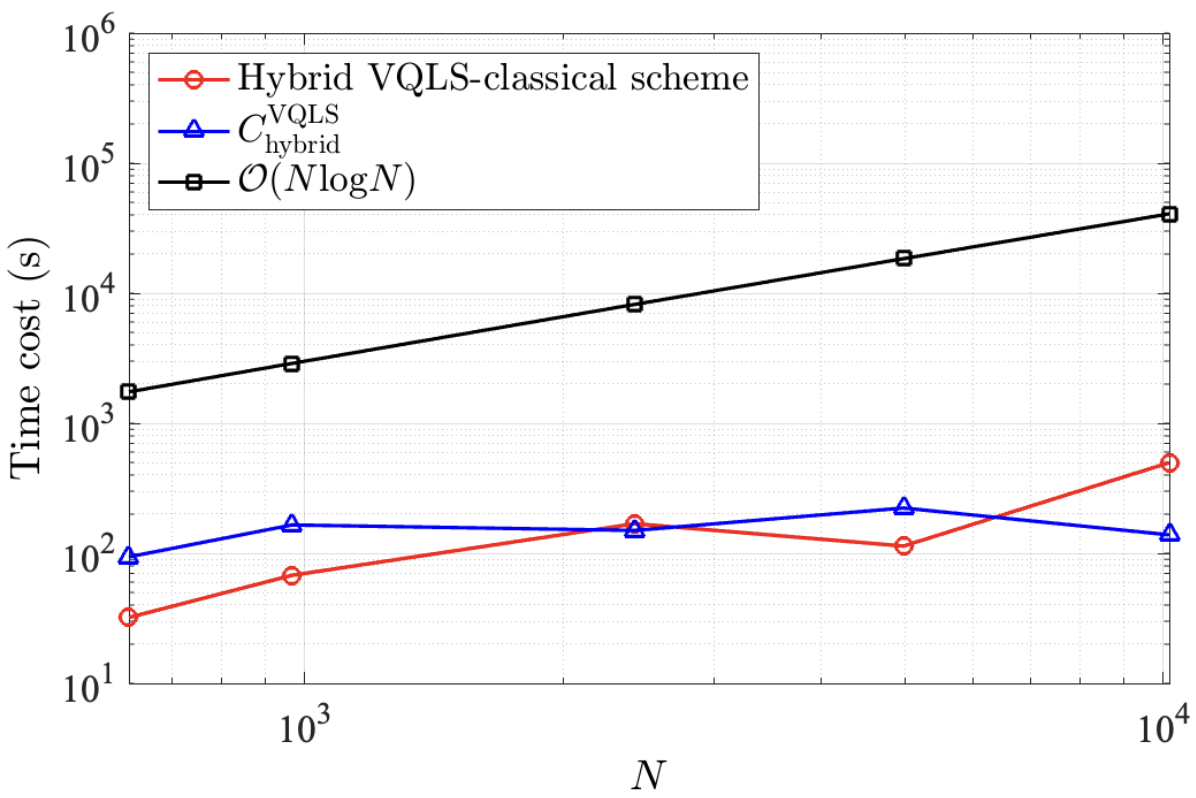
В статье представлено исследование точности и производительности гибридной схемы для решения интегральных уравнений электромагнитного поля с использованием квантовых алгоритмов, таких как HHL и VQLS, и методов предварительной обработки.

Традиционные численные методы решения интегральных уравнений электромагнитного поля сталкиваются с ограничениями масштабируемости при анализе сложных объектов. В работе, озаглавленной ‘Solution of the Electric Field Integral Equation Using a Hybrid Quantum-Classical Scheme: Investigation of Accuracy and Efficiency’, предложен гибридный квантово-классический алгоритм, сочетающий преимущества классических методов предобуславливания и квантовых алгоритмов для решения полученных линейных систем. Полученные результаты демонстрируют потенциальное снижение вычислительной сложности по сравнению с классическими подходами, особенно для задач большого масштаба. Возможно ли, таким образом, расширить границы применимости численных методов в вычислительной электромагнетике и решить задачи, недоступные для классических компьютеров?

---

Электромагнитное Моделирование: Узкое Горлышко Вычислений

Анализ электромагнитного рассеяния с использованием традиционных методов, таких как поверхностные интегральные уравнения, неизбежно приводит к возникновению вычислительно затратных систем плотных матричных уравнений. Этот подход требует решения систем, где количество неизвестных растет пропорционально $N^2$, где $N$ — число дискретных элементов на моделируемой поверхности. В результате, даже для структур умеренной сложности, требуется значительный объем вычислительных ресурсов и памяти для хранения и обработки этих плотных матриц. Это ограничивает возможность моделирования сложных, реалистичных объектов и требует поиска альтернативных, более эффективных вычислительных стратегий для анализа электромагнитного рассеяния.

Прямые методы решения, несмотря на свою высокую точность, сталкиваются с серьезными ограничениями при моделировании сложных электромагнитных структур. Суть проблемы заключается в кубической сложности $O(N^3)$ — время вычислений и требуемая память растут пропорционально кубу числа неизвестных $N$. Это означает, что даже умеренное увеличение размера модели, например, увеличение числа элементов сетки, приводит к экспоненциальному росту вычислительной нагрузки. В результате, моделирование крупных и детализированных структур, таких как антенные решетки сложной формы или биологические ткани, становится практически невозможным на современных вычислительных ресурсах, требуя либо чрезмерно долгого времени вычислений, либо недоступного объема памяти.

Итеративные решатели, несмотря на свою теоретическую эффективность, выражающуюся в сложности $O(NlogN)$, часто сталкиваются с практическими ограничениями. В отличие от прямых решателей, требующих значительных вычислительных ресурсов, итеративные методы нуждаются в большом объеме памяти для хранения промежуточных результатов и векторов состояния. Более того, скорость их сходимости может существенно снижаться при решении сложных задач, особенно для структур с высокой контрастностью материалов или сложной геометрией. Это требует применения сложных стратегий предобуславливания и адаптивных алгоритмов ускорения сходимости, что усложняет процесс моделирования и увеличивает время, необходимое для получения точных результатов электромагнитного анализа.

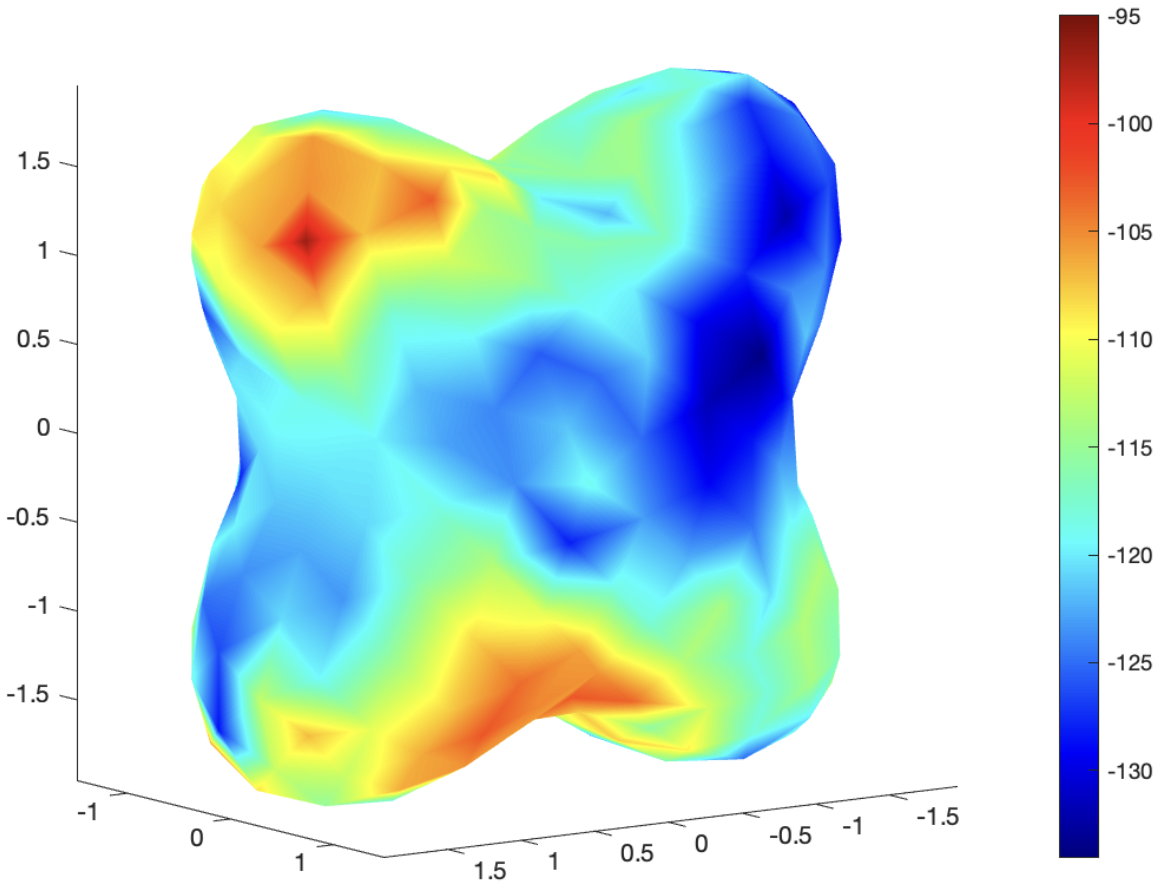
Квантовые Вычисления: Луч Надежды в Расчетных Задачах

Квантовые вычисления, использующие принципы суперпозиции и запутанности, потенциально обеспечивают экспоненциальное ускорение определенных вычислений. В отличие от классических битов, которые могут представлять только 0 или 1, кубиты, благодаря суперпозиции, могут одновременно существовать в состояниях 0, 1 и их комбинациях. Запутанность позволяет коррелировать состояния нескольких кубитов, что позволяет параллельно выполнять операции над большим объемом данных. Это фундаментальное отличие позволяет квантовым алгоритмам, таким как алгоритм Шора для факторизации больших чисел или алгоритм Гровера для поиска в несортированной базе данных, демонстрировать теоретическое экспоненциальное ускорение по сравнению с лучшими известными классическими алгоритмами. Следует отметить, что не все вычислительные задачи поддаются такому ускорению, и эффективность квантовых вычислений сильно зависит от структуры решаемой задачи.

В отличие от классического бита, который может находиться только в состоянии 0 или 1, кубит использует принципы квантовой механики, такие как суперпозиция, для представления информации. Это позволяет кубиту существовать в комбинации состояний 0 и 1 одновременно. В результате, для хранения $n$ кубитов требуется лишь $lo{g}_2(n)$ битов классической памяти для описания их состояния, что обеспечивает логарифмическую сложность хранения по сравнению с линейной сложностью классических битов. Таким образом, увеличение количества кубитов не требует пропорционального увеличения объема необходимой классической памяти для их описания, что является ключевым преимуществом квантовых вычислений при работе с большими объемами данных.

Алгоритм HHL (Harrow-Hassidim-Lloyd) представляет собой квантовый алгоритм, предназначенный для решения систем линейных уравнений $Ax=b$ в определенных условиях. В отличие от классических методов, таких как метод Гаусса, HHL потенциально может обеспечить экспоненциальное ускорение при решении этих систем, при условии, что матрица $A$ является разреженной и хорошо обусловленной, а вектор $b$ может быть эффективно загружен в квантовое состояние. Это особенно актуально для электромагнитного моделирования, где решение больших систем линейных уравнений является вычислительно затратной задачей. Ускорение достигается за счет использования квантовых принципов суперпозиции и запутанности, позволяющих параллельно обрабатывать множество возможных решений.

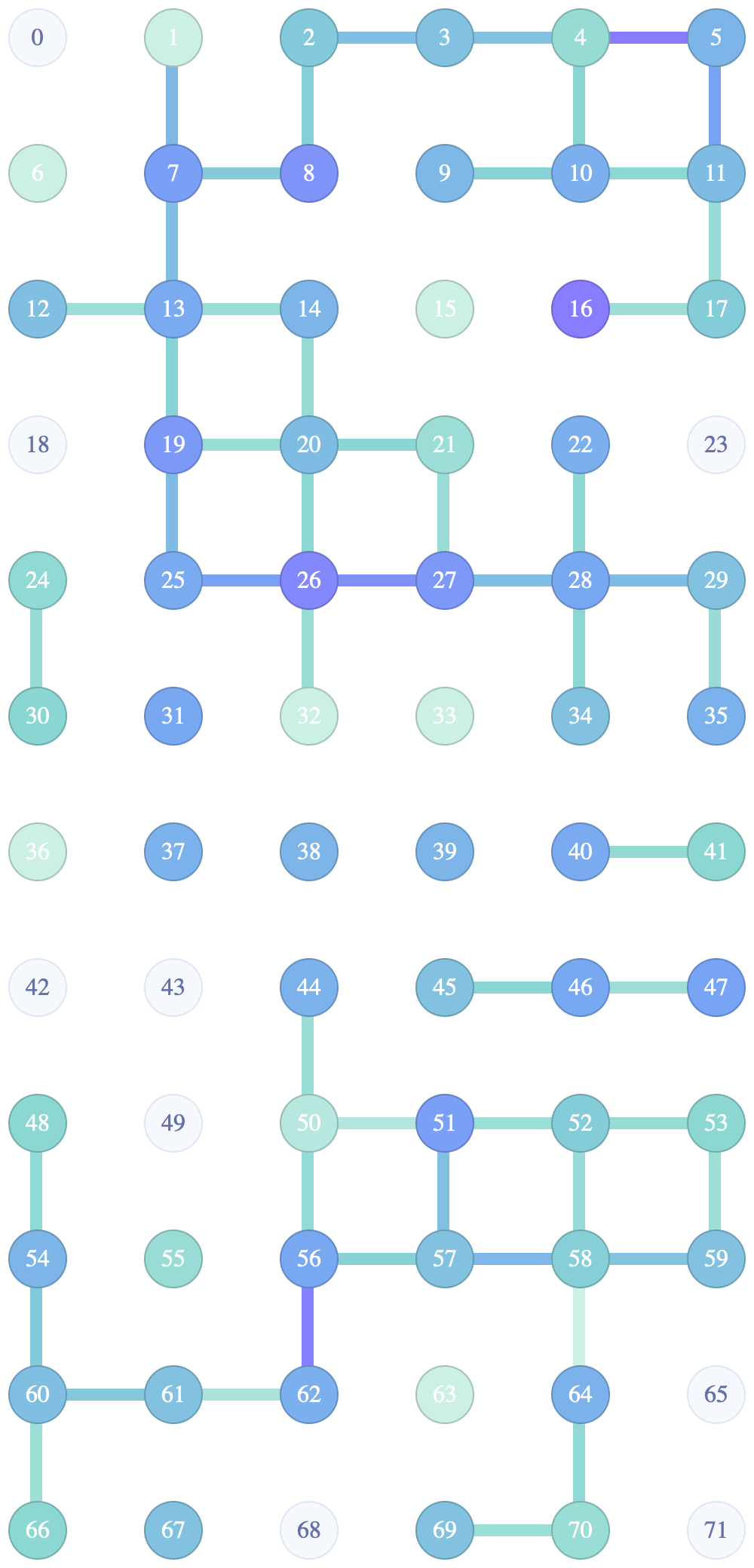
Гибридные Схемы: Сочетание Классики и Кванта для Практического Применения

Гибридные квантово-классические схемы используют преимущества обеих парадигм вычислений, применяя классические методы понижения размерности для эффективной обработки сложных задач. Суть подхода заключается в использовании классических алгоритмов для предварительной обработки данных и уменьшения размерности решаемой задачи до величины, доступной для квантовых алгоритмов. Это позволяет преодолеть ограничения, связанные с текущим количеством кубитов и их когерентностью, и эффективно применять квантовые вычисления к задачам, которые в противном случае были бы невыполнимы. Понижение размерности достигается посредством проецирования исходной системы в подпространство меньшей размерности, сохраняя при этом наиболее важные характеристики решаемой задачи.

Двухуровневая итеративная стратегия позволяет эффективно применять квантовые алгоритмы, такие как VQLS и HHL, за счет преобразования исходной системы в меньшие подпространства. Этот подход предполагает последовательное отображение исходной задачи в подпространство меньшей размерности, что снижает требования к количеству кубитов и глубине квантовой цепи. Итеративный процесс позволяет повторно уточнять решение, постепенно приближаясь к точному ответу, при этом сохраняя вычислительную эффективность. Использование подпространств существенно уменьшает сложность вычислений, делая применение квантовых алгоритмов более реалистичным для задач, которые в противном случае были бы неразрешимы на доступном квантовом оборудовании.

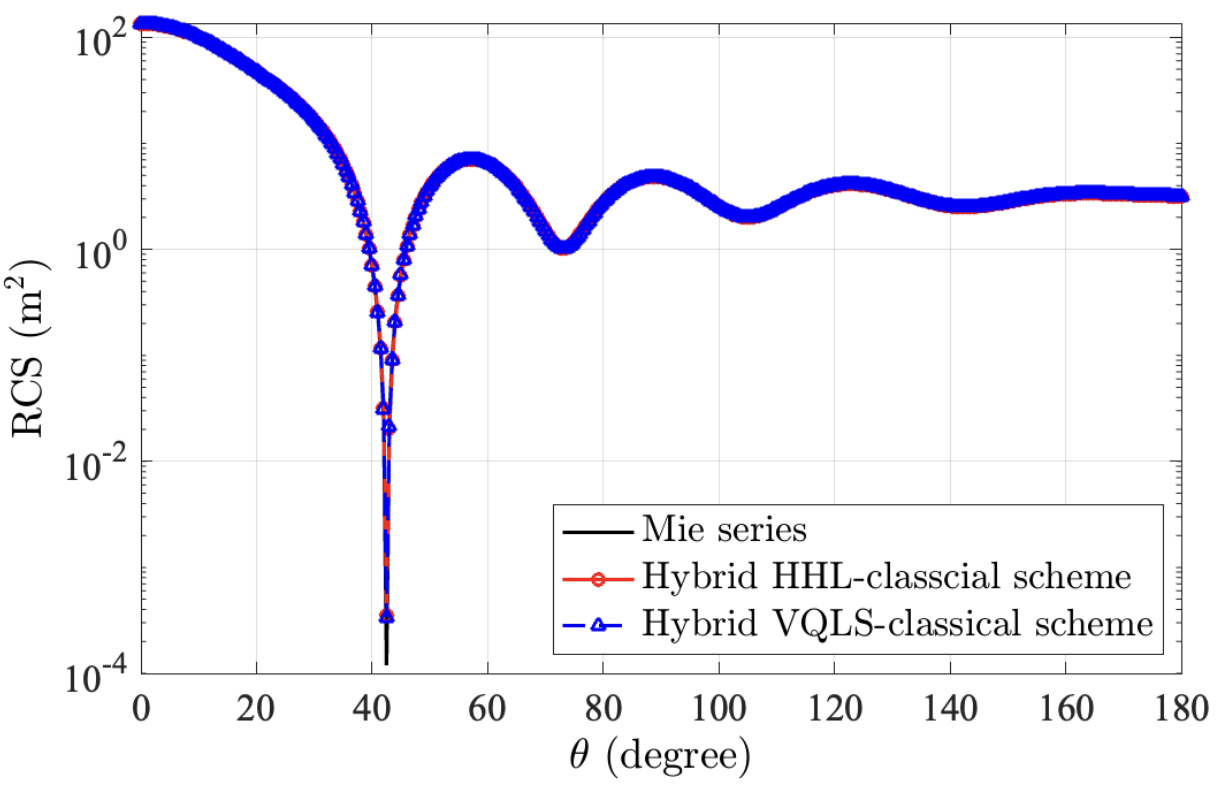
При валидации на реальном квантовом оборудовании, гибридная схема показала относительные погрешности RCS до $1.502\times 10^{-5}$. На квантовых симуляторах достигнуты показатели относительной погрешности в $0.0047$ и $0.0049$ соответственно. Характеристики использованного квантового оборудования включают в себя точность однокубитных гейтов $0.9972$, точность двухкубитных гейтов $0.9629$, и точность считывания $0.8736$. Данные результаты демонстрируют возможность достижения высокой точности при использовании гибридных квантово-классических схем даже на оборудовании с ограниченными характеристиками.

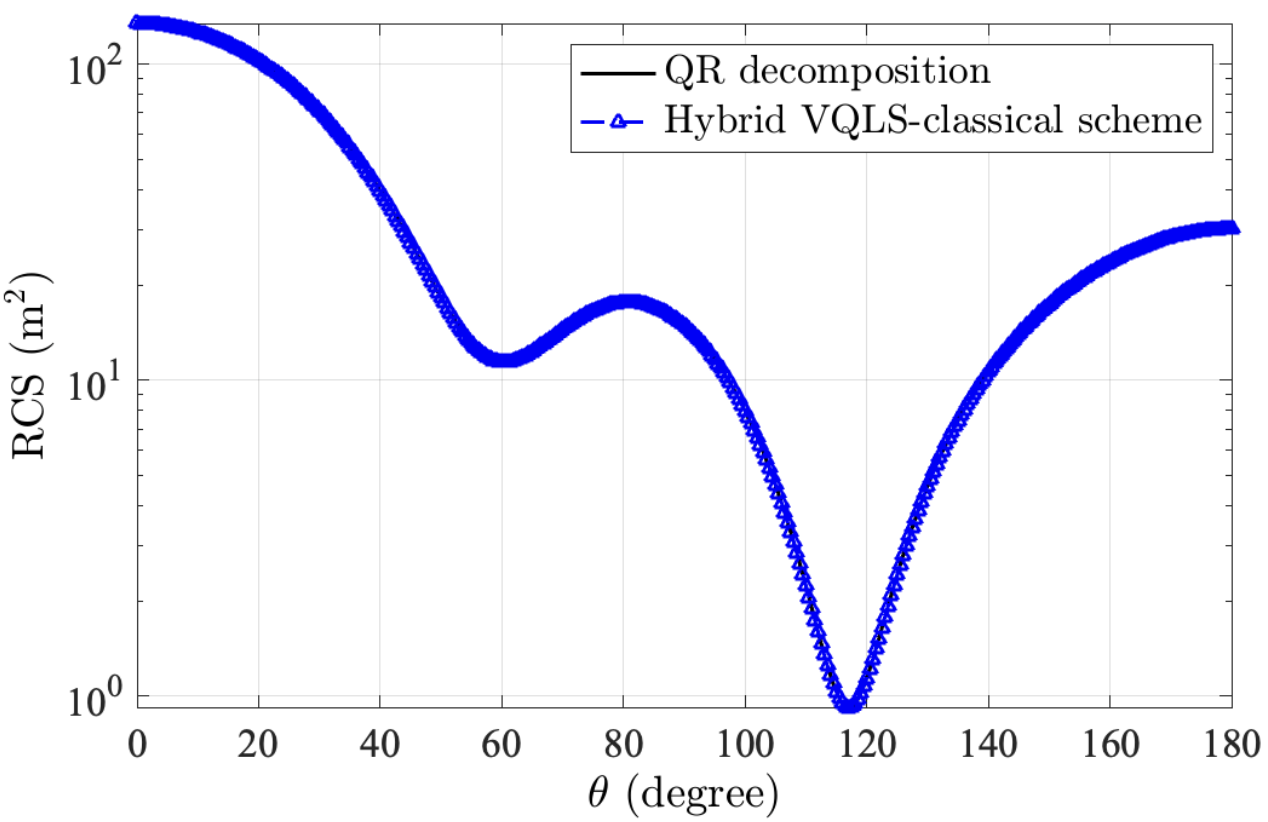
Расширяя Горизонты: Области Применения и Перспективы Развития

Точное и эффективное вычисление эффективной площади рассеяния (ЭПР), имеющее критическое значение для систем обороны и наблюдения, получает прямое преимущество от представленных разработок. Способность моделировать сложные сценарии рассеяния электромагнитных волн с повышенной скоростью и точностью позволяет создавать более совершенные радары и системы обнаружения. Это, в свою очередь, способствует улучшению возможностей идентификации целей, снижению ложных срабатываний и повышению общей надежности систем безопасности. Улучшенные алгоритмы, основанные на методе моментов и усиленные квантовыми вычислениями, открывают перспективы для анализа объектов сложной геометрии и материалов, что особенно важно при разработке технологий невидимости и противодействия радарам. В конечном итоге, эти достижения в области вычислительной электродинамики оказывают существенное влияние на развитие оборонной промышленности и повышение национальной безопасности.

Интеграция квантовых алгоритмов с методом моментов, осуществляемая посредством моделирования Гамильтона, открывает принципиально новые возможности для анализа сложных задач рассеяния. Традиционные численные методы, применяемые для расчета радиолокационной отражающей способности объектов, часто сталкиваются с ограничениями при моделировании структур сложной геометрии или материалов. Использование квантовых алгоритмов, в частности, основанных на моделировании Гамильтона, позволяет эффективно решать системы линейных уравнений, возникающие при применении метода моментов, экспоненциально сокращая время вычислений для определенных классов задач. Это особенно важно при анализе рассеяния электромагнитных волн на объектах сложной формы, где традиционные методы становятся вычислительно затратными или вовсе непрактичными. Возможность эффективного моделирования рассеяния открывает перспективы для создания более точных систем радиолокации и наблюдения, а также для разработки новых материалов с заданными электромагнитными характеристиками. Эффективность предложенного подхода зависит от возможностей реализации квантовых алгоритмов на современных и перспективных квантовых вычислительных устройствах.

Для полной реализации потенциала гибридных схем, объединяющих классические и квантовые вычисления, необходимы дальнейшие исследования в области квантового оборудования, в частности, разработка и совершенствование реальных квантовых компьютеров. Помимо аппаратного обеспечения, критически важна оптимизация квантовых алгоритмов, применяемых для расчета радиолокационной отражающей способности, что позволит значительно повысить скорость и точность моделирования сложных сценариев рассеяния. Разработка более эффективных алгоритмов, способных эффективно использовать ограниченные ресурсы существующих и будущих квантовых устройств, станет ключевым фактором для практического применения этих методов в оборонной промышленности и системах наблюдения. Прогресс в этой области откроет возможности для анализа объектов с беспрецедентной детализацией и разработки более совершенных систем обнаружения и слежения.

Исследование, представленное в данной работе, напоминает попытку заглянуть за горизонт событий, используя вычислительные методы. Авторы стремятся решить сложную задачу электромагнитного рассеяния, комбинируя квантовые и классические подходы. Каждая итерация предложенного гибридного алгоритма — это попытка поймать неуловимое, приблизить решение к реальности, однако, подобно черной дыре, абсолютная точность остается недостижимой. Как заметил Луи де Бройль: «Всякая волна обладает корпускулярными свойствами, и наоборот». Этот принцип, хоть и относится к физике частиц, прекрасно иллюстрирует суть гибридных алгоритмов — объединение различных подходов для достижения результата, который недостижим при использовании только одного из них. Предобуславливание линейных систем, являющееся ключевым аспектом исследования, лишь подчеркивает стремление к оптимизации и повышению эффективности вычислений, подобно попытке уменьшить сингулярность в центре черной дыры.

Что дальше?

Представленная работа, как и многие другие, пытается приручить квантового зверя для решения задач, которые классическим машинам даются с трудом. Идея — не нова, но само воплощение, попытка гибридного подхода, заслуживает внимания. Однако, не стоит обольщаться: элегантные схемы на бумаге часто разбиваются о скалы реальных данных. Предобуславливание, решение линейных систем — всё это прекрасно, пока не столкнёшься с шумом, декогеренцией, и конечно, с неизбежной сложностью масштабирования. Физика — это искусство догадок под давлением космоса, и каждая «универсальная» схема рано или поздно находит своё ограничение.

Настоящий вызов — не в скорости вычислений, а в понимании того, где квантовые алгоритмы действительно превзойдут классические. Электромагнитное рассеяние — лишь одна из многих задач. Более глубокий вопрос — как эффективно использовать ограниченные квантовые ресурсы, как бороться с ошибками, и как разрабатывать алгоритмы, устойчивые к несовершенству квантового оборудования. Чёрная дыра — это не просто объект, это зеркало нашей гордости и заблуждений.

Вполне вероятно, что будущее подобных исследований лежит не в погоне за абсолютной скоростью, а в разработке специализированных квантовых ускорителей, дополняющих классические вычисления. И возможно, когда-нибудь, мы сможем не только решать сложные уравнения, но и по-настоящему понимать физику, лежащую в их основе. Но пока это — лишь одна из бесконечных догадок.

---

Оригинал статьи: https://arxiv.org/pdf/2512.03808.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/