Квантовое машинное обучение: новый горизонт масштабируемости

---

Исследование демонстрирует, что использование многофотонных состояний в линейных оптических схемах значительно повышает обучаемость квантовых моделей.

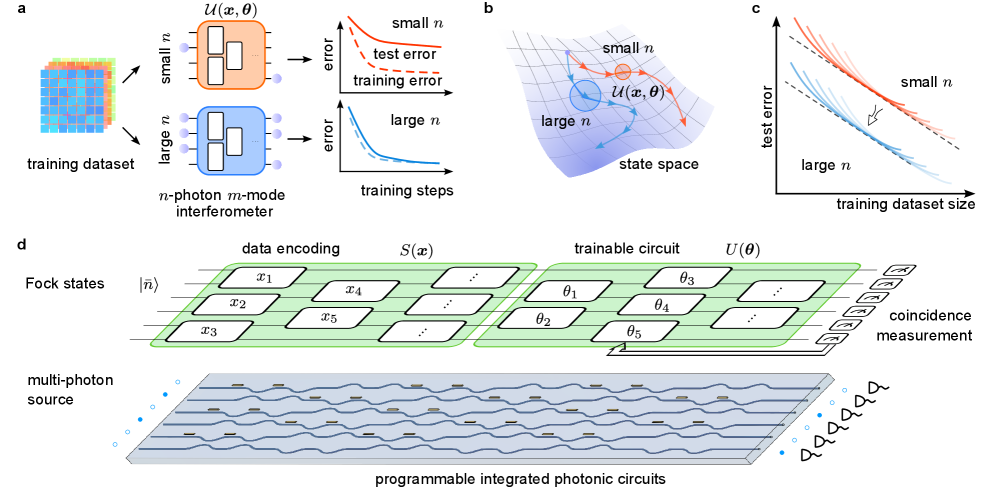
Многофотонные состояния в линейной оптике позволяют снизить требования к объему обучающих данных и улучшить обобщающую способность алгоритмов квантового машинного обучения, включая обучение метрикам и унитарным преобразованиям.

Несмотря на значительный прогресс в области квантовых вычислений, эффективное использование многофотонных состояний для задач машинного обучения остаётся сложной задачей. В работе, озаглавленной ‘A scalable advantage in multi-photon quantum machine learning’, исследуется возможность масштабирования преимуществ квантового машинного обучения с использованием многофотонных состояний. Показано, что ёмкость обучения линейных оптических схем растёт полиномиально с числом фотонов, что позволяет снизить требования к объёму обучающих данных и повысить обобщающую способность моделей. Открывает ли это путь к созданию практически применимых квантовых алгоритмов машинного обучения, превосходящих классические аналоги?

---

Квантовое машинное обучение: От сложности к ясности

Традиционные алгоритмы машинного обучения сталкиваются с серьезными трудностями при обработке данных высокой размерности и сложности. По мере увеличения числа признаков, необходимых для точного моделирования, вычислительные затраты и объем требуемых данных экспоненциально возрастают, что приводит к проблеме “проклятия размерности”. В результате, обучение моделей становится непрактичным или требует огромных вычислительных ресурсов. Это особенно актуально в таких областях, как обработка изображений, анализ генома и финансовое моделирование, где данные часто характеризуются тысячами или даже миллионами признаков. Существующие методы, такие как понижение размерности, могут помочь смягчить проблему, но они часто приводят к потере информации и снижению точности модели. Поэтому поиск новых подходов, способных эффективно обрабатывать сложные и многомерные данные, является критически важной задачей в современной науке о данных.

Квантовое машинное обучение (КМО) представляет собой перспективное направление, использующее принципы квантовой механики для решения задач, непосильных классическим алгоритмам. В отличие от традиционных методов, где информация кодируется в битах, КМО оперирует с кубитами, способными находиться в суперпозиции состояний и использовать явление запутанности. Это позволяет квантовым моделям экспоненциально увеличивать вычислительные возможности при обработке больших объемов данных и решении сложных оптимизационных задач. Преимущества КМО особенно заметны при анализе многомерных данных, где классические алгоритмы сталкиваются с проблемой “проклятия размерности”, а квантовые модели способны находить закономерности и делать прогнозы значительно быстрее и точнее. Таким образом, КМО открывает новые горизонты в областях, требующих обработки огромных массивов информации, таких как распознавание образов, финансовое моделирование и открытие новых материалов.

Ключевым фактором повышения обучаемости квантовых моделей является использование многофотонных состояний. В отличие от классических систем, оперирующих битами, квантовые вычисления используют кубиты, способные находиться в суперпозиции состояний. Однако, для решения сложных задач требуется значительно больше кубитов. Использование многофотонных состояний, где каждый фотон представляет собой кубит, позволяет эффективно кодировать и обрабатывать информацию, значительно расширяя возможности квантовой модели. Такой подход позволяет создавать более сложные и выразительные квантовые схемы, способные улавливать тонкие зависимости в данных и повышать точность прогнозов. Исследования показывают, что увеличение числа фотонов в многофотонном состоянии напрямую влияет на способность модели к обобщению и решению задач, недоступных классическим алгоритмам. Более того, манипулирование этими состояниями открывает новые горизонты в разработке квантовых нейронных сетей и алгоритмов машинного обучения.

Разработка эффективных методов обучения квантовых схем для выполнения сложных задач является ключевым шагом на пути к практическому применению квантового машинного обучения. Традиционные алгоритмы машинного обучения часто требуют экспоненциально растущего объема данных для достижения высокой точности, что становится серьезным ограничением при работе с большими и сложными наборами данных. Исследователи стремятся создать такие методы обучения, которые позволят квантовым моделям достигать аналогичной или превосходящей точности, используя при этом лишь постоянное количество обучающих данных. Это достигается за счет использования уникальных свойств квантовой механики, таких как суперпозиция и запутанность, для более эффективного представления и обработки информации. Успешная реализация подобного подхода не только значительно снизит вычислительные затраты, но и откроет новые возможности для решения задач, недоступных классическим алгоритмам, особенно в областях, где получение больших объемов данных затруднено или невозможно.

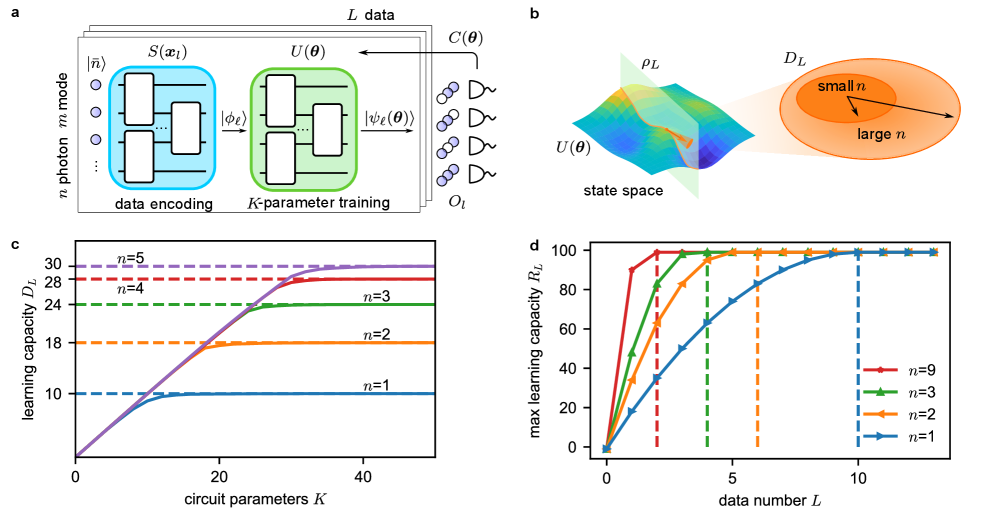
Единое преобразование: Путь к квантовому решению

Метод обучения на основе унитарных преобразований представляет собой подход к тренировке квантовых схем с целью аппроксимации целевых унитарных преобразований. В рамках данного подхода, параметры квантовой схемы оптимизируются таким образом, чтобы выходное состояние схемы максимально соответствовало желаемому целевому состоянию, определяемому целевым унитарным преобразованием $U_{target}$. Обучение включает в себя минимизацию функции потерь, которая количественно определяет разницу между выходным состоянием обученной схемы и целевым состоянием. Этот процесс позволяет эффективно находить параметры схемы, реализующие заданное унитарное преобразование, что является ключевым для решения различных задач квантовых вычислений.

Параметризованные линейно-оптические схемы (Linear Optical Quantum Circuits, LOQC) представляют собой гибкую платформу для реализации квантовых схем, использующих фотонные кубиты. Эти схемы строятся на основе манипулирования фотонными состояниями, такими как число фотонов, и используют линейные оптические элементы, такие как лучеделители и фазовращатели. В отличие от схем, требующих нелинейных взаимодействий, LOQC полагаются на вероятностные измерения и пост-селекцию, что позволяет создавать универсальные квантовые вычисления, хотя и с определенными ограничениями по эффективности. Параметризация элементов схемы, например, углов поворота поляризации или коэффициентов отражения/пропускания, позволяет настраивать схему для выполнения различных квантовых операций и алгоритмов. Использование фотонных кубитов обеспечивает когерентность и низкий уровень шума, что делает LOQC перспективной платформой для реализации квантовых алгоритмов, особенно в области квантовой обработки информации и коммуникаций.

В основе работы параметризованных линейно-оптических схем лежит манипулирование фотонными состояниями числа фотонов для кодирования и обработки информации. Вместо использования кубитов, представляющих собой суперпозиции состояний 0 и 1, эти схемы оперируют с дискретными состояниями, определяемыми числом фотонов в определенном режиме. Информация кодируется посредством создания и изменения этих фотонных состояний, используя такие элементы, как сдвигатели фазы и разветвители пучка. Выполнение квантовых вычислений сводится к последовательному применению унитарных преобразований к этим состояниям числа фотонов, что позволяет выполнять операции, эквивалентные квантовым логическим элементам. Измерение числа фотонов после выполнения операций позволяет извлечь закодированную информацию и определить результат вычислений.

Эффективное обучение квантовых схем требует точного контроля и измерений, часто реализуемых посредством регистрации совпадений (coincidence counting). Этот метод позволяет значительно сократить объем необходимых обучающих данных. В традиционных подходах потребность в данных растет линейно с количеством параметров задачи, обозначаясь как $O(m)$. Однако, применение регистрации совпадений позволяет снизить эту потребность до $O(1)$, то есть независимой от количества параметров, что существенно повышает эффективность обучения и снижает вычислительные затраты.

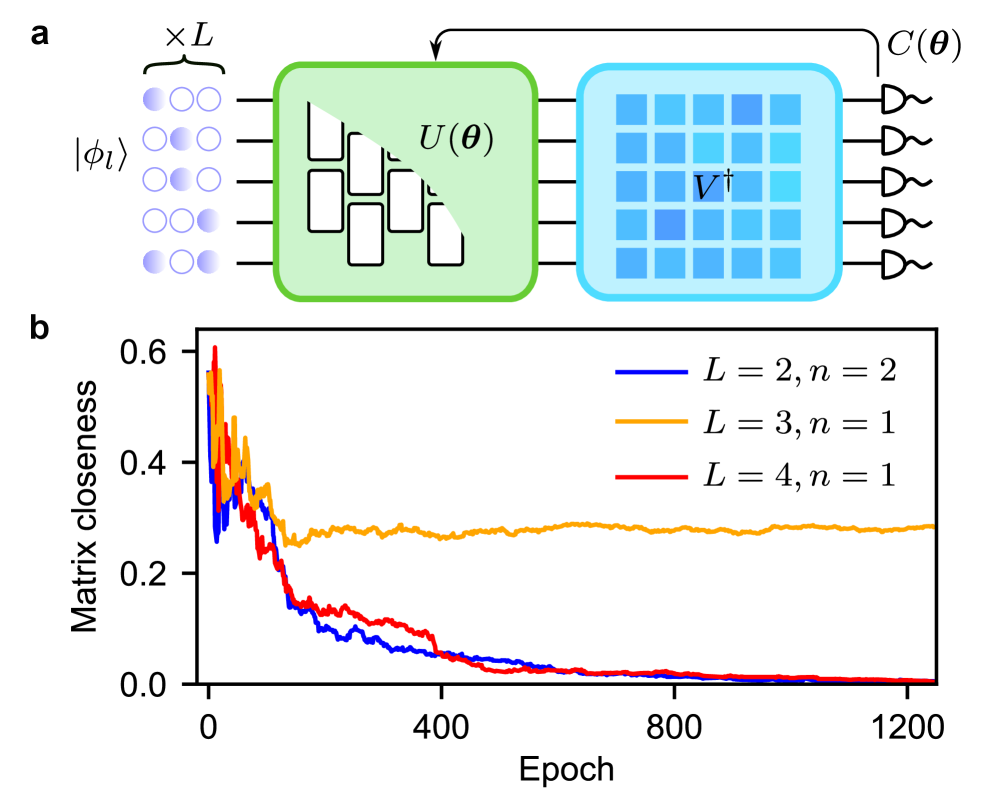
Интегрированная фотоника: Путь к масштабируемым квантовым системам

Интегрированные фотонные схемы являются ключевым элементом для масштабирования и практической реализации моделей квантового машинного обучения. Традиционные электронные схемы сталкиваются с ограничениями по скорости и энергопотреблению при обработке больших объемов данных, необходимых для обучения сложных квантовых моделей. Фотонические схемы, напротив, используют фотоны для передачи и обработки информации, что позволяет значительно увеличить скорость вычислений и снизить энергопотребление. Масштабируемость обеспечивается за счет возможности плотной интеграции множества оптических компонентов на одном чипе, позволяя создавать сложные квантовые схемы, необходимые для обучения и развертывания эффективных алгоритмов машинного обучения. Использование интегрированных фотонных схем позволяет преодолеть ограничения, связанные с размером и сложностью квантовых систем, что является необходимым условием для практического применения квантового машинного обучения.

Технология записи волноводов с использованием фемтосекундного лазера представляет собой надежный метод создания интегрированных фотонных схем непосредственно на чипе. В процессе, сфокусированный фемтосекундный лазерный импульс индуцирует локальные изменения показателя преломления в диэлектрическом материале, таком как стекло или сапфир. Эти изменения формируют волноводы, по которым распространяется свет. Преимуществами данного метода являются его гибкость, позволяющая создавать сложные трехмерные структуры, относительно низкая стоимость и совместимость с существующими технологиями микроэлектроники. Разрешение, достигаемое при использовании фемтосекундных лазеров, позволяет создавать волноводы с размерами порядка нескольких микрометров, что необходимо для интеграции с другими оптическими и электронными компонентами. Параметры лазера, включая длину импульса, мощность и скорость сканирования, точно контролируются для обеспечения требуемых характеристик волноводов, таких как длина, ширина и форма.

Оптические переключатели являются ключевыми компонентами в интегральных фотонных схемах, обеспечивая динамическое управление путями фотонов. Эти устройства, как правило, основаны на эффектах, таких как эффект Керра или электрооптический эффект, позволяя изменять показатели преломления материала под воздействием внешних факторов, например, электрического поля или интенсивности света. В контексте квантовых вычислений, переключатели используются для маршрутизации одиночных фотонов между различными квантовыми битами (кубитами) или для реализации логических операций, необходимых для выполнения квантовых алгоритмов. Контроль над направлением фотонов позволяет создавать сложные оптические цепи, необходимые для масштабируемых квантовых систем, а также для реализации программируемых квантовых схем.

Манипулирование структурой интегрированных фотонных схем позволяет реализовать локальные фазовые унитарные преобразования, являющиеся ключевым элементом многих квантовых алгоритмов. Эти преобразования, представленные в виде $U=e^{i\varphi }$, изменяют фазу фотона без изменения его амплитуды, что необходимо для кодирования и обработки квантовой информации. Точное управление фазой позволяет выполнять операции над кубитами, необходимые для реализации квантовых вентилей, таких как фазовый сдвиг и вращения, и, следовательно, для построения сложных квантовых цепей. Использование интегрированной фотоники для реализации этих преобразований обеспечивает высокую стабильность, масштабируемость и точность, необходимые для практического применения квантовых вычислений.

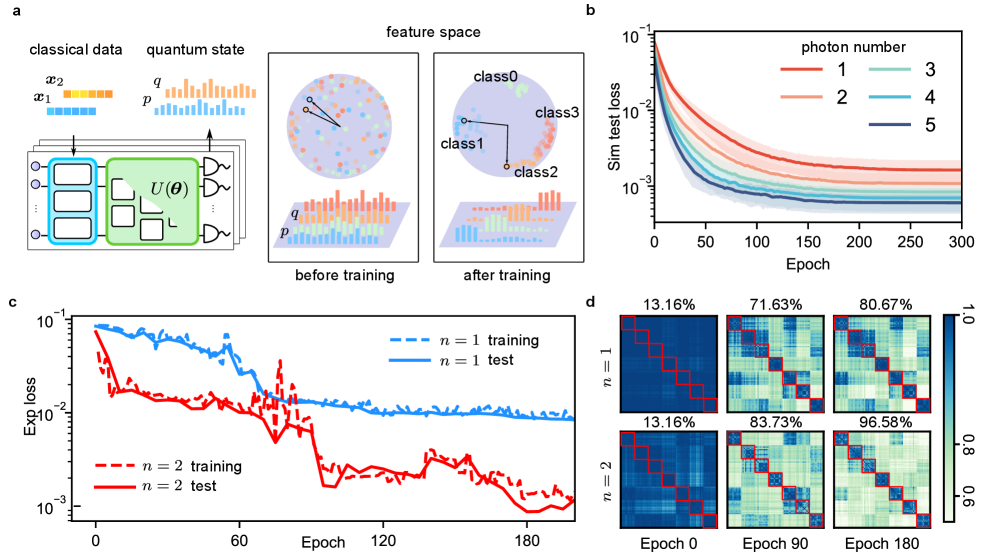
Квантовое обучение метрик: Распознавание гласных как демонстрация возможностей

Возможность обучения квантовых схем метрическому представлению данных открывает новые горизонты в обработке информации. В основе этого подхода лежит способность схемы вычислять функцию расстояния между различными точками данных, что позволяет ей эффективно различать и классифицировать объекты. В отличие от традиционных методов, где метрика задается вручную, квантовое обучение метрики позволяет схеме самостоятельно адаптировать эту функцию на основе предоставленных данных. Это достигается за счет манипулирования квантовыми состояниями таким образом, чтобы близкие по характеристикам данные отображались в близкие квантовые состояния, а отдаленные — в отдаленные. Такой подход позволяет эффективно решать задачи классификации, кластеризации и поиска ближайших соседей, особенно в ситуациях, когда данные имеют высокую размерность или сложную структуру. В результате, квантовое обучение метрике представляет собой мощный инструмент для создания интеллектуальных систем, способных к адаптации и обучению на основе данных.

Для демонстрации возможностей квантового обучения метрики была проведена задача распознавания гласных звуков, используя стандартный набор данных для этой цели. В рамках исследования, модель обучалась различать различные гласные, основываясь на извлеченных характеристиках из аудиозаписей. Успешное выполнение этой задачи подтверждает потенциал квантовых схем в обработке и классификации звуковых сигналов, открывая перспективы для разработки более эффективных систем распознавания речи и других приложений, связанных с анализом звука. Полученные результаты позволяют предположить, что квантовые алгоритмы способны выявлять тонкие различия в акустических характеристиках, что приводит к повышению точности распознавания.

В рамках исследования распознавания гласных звуков, в качестве входных данных для квантовой модели используются формантные частоты, извлеченные из аудиозаписей. Формантные частоты представляют собой резонансные частоты речевого тракта, которые служат уникальными акустическими характеристиками каждого гласного. Преобразование звуковых волн в эти частоты позволяет квантовой модели оперировать с компактным и информативным представлением речевого сигнала. Использование формантных частот, а не сырых аудиоданных, значительно снижает вычислительную сложность и повышает эффективность обучения модели, позволяя ей более точно различать различные гласные звуки и демонстрировать потенциал квантового машинного обучения в задачах обработки речи.

Исследования показали, что применение перестановок мод в квантовых схемах машинного обучения метрик значительно повышает точность распознавания гласных. В процессе обучения, оптимизация происходит за счет эффективного использования различных мод фотонов, что позволяет модели лучше различать признаки, извлеченные из аудиозаписей — в данном случае, частоты формант. Эксперименты продемонстрировали, что использование перестановок мод позволяет достичь более высокой тестовой точности по сравнению с моделями, использующими однофотонные состояния, указывая на важность манипулирования квантовыми состояниями для улучшения производительности алгоритмов машинного обучения.

Исследование демонстрирует, что использование многофотонных состояний в линейных оптических схемах значительно расширяет возможности квантовых моделей машинного обучения. Подобный подход к обучению, когда данные используются максимально эффективно, перекликается с философией упрощения и ясности. Как однажды заметил Ричард Фейнман: «Если вы не можете объяснить что-то простыми словами, значит, вы сами этого не понимаете». По сути, данная работа стремится к элегантности в обучении, минимизируя потребность в больших объемах данных и повышая обобщающую способность алгоритмов, особенно в задачах, как метрическое обучение и обучение унитарным преобразованиям. Истинное совершенство достигается не в сложности, а в способности выжать максимум из минимума.

Что дальше?

Представленная работа демонстрирует, что использование многофотонных состояний в линейной оптике действительно способно повысить обучающую способность квантовых машин, сокращая потребность в больших объемах данных. Однако, эта победа над сложностью не должна затмевать лежащие в основе ограничения. Вопрос не в том, чтобы наращивать количество фотонов, а в том, чтобы извлекать максимум информации из каждого. Иначе, мы просто заменим один вид шума другим.

Очевидным направлением дальнейших исследований является поиск более элегантных и компактных схем, позволяющих создавать и манипулировать многофотонными состояниями. Текущие реализации, как правило, громоздки и чувствительны к ошибкам. Совершенство заключается не в увеличении масштаба, а в минимализме. Задача состоит в том, чтобы создать систему, в которой сложность алгоритма компенсируется простотой реализации.

В конечном счете, ценность данной работы заключается не в достигнутых результатах, а в поставленных вопросах. Возможно ли принципиально улучшить обобщающую способность квантовых алгоритмов, или мы обречены на повторение ошибок классического машинного обучения, просто с использованием другого физического субстрата? Истинный прогресс достигается не тогда, когда мы находим ответы, а когда начинаем задавать правильные вопросы.

---

Оригинал статьи: https://arxiv.org/pdf/2511.21951.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/