Квантовое моделирование нелинейных систем: новый подход

---

Исследователи предлагают использовать квантовые компьютеры с непрерывными переменными для эффективной симуляции сложных нелинейных процессов, открывая возможности для решения задач, недоступных классическим вычислительным системам.

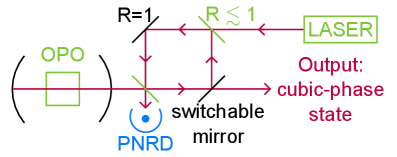
В статье рассматривается применение формализма Купмана-Неймана к фотонным квантовым компьютерам непрерывных переменных для моделирования динамики, в частности, уравнения Кортевега-де Вриса.

Несмотря на успехи в моделировании сложных систем, классические вычислительные подходы сталкиваются с ограничениями при анализе нелинейной динамики. В работе, посвященной ‘Implementing the Koopman-von Neumann approach on continuous-variable photonic quantum computers’, исследуется применение формализма Купмана-Неймана к квантовым вычислениям на основе непрерывных переменных. Показано, что данный подход позволяет эффективно отображать классические уравнения, такие как уравнение Кортевега-де Вриса, на квантовые фотонные платформы, потенциально обеспечивая ускорение симуляций. Сможет ли сочетание квантовых технологий и формализма Купмана-Неймана открыть новые горизонты в моделировании и прогнозировании сложных нелинейных систем?

---

За гранью классики: поиск новых путей моделирования

Многие физические системы, такие как гидродинамика и турбулентность, по своей природе классические, однако их математическое описание часто выходит за рамки простых аналитических решений. Даже при наличии точных уравнений, описывающих поведение жидкости или газа, поиск точных решений оказывается чрезвычайно сложным, а иногда и невозможным. Это связано с нелинейностью уравнений, описывающих эти системы, и с возникновением сложных взаимодействий между различными масштабами движения. В результате, для понимания и прогнозирования поведения таких систем приходится прибегать к численному моделированию, которое, несмотря на значительные успехи, сталкивается с ограничениями по вычислительным ресурсам и точности, особенно при моделировании долгосрочных процессов и сложных турбулентных течений. Именно эта сложность стимулирует поиск новых подходов к моделированию классических систем, позволяющих преодолеть ограничения традиционных методов.

Традиционные численные методы, несмотря на свою широкую распространенность, сталкиваются со значительными трудностями при моделировании сложных физических систем. Это особенно заметно в задачах, связанных с динамикой жидкостей и газов, где нелинейность уравнений и турбулентность приводят к экспоненциальному росту вычислительных затрат. Даже с использованием мощнейших суперкомпьютеров, долгосрочное предсказание поведения таких систем остается проблематичным, поскольку ошибки округления и дискретизации быстро накапливаются. Вследствие этого, возникает потребность в разработке принципиально новых подходов к численному моделированию, способных преодолеть ограничения классических методов и обеспечить более точные и надежные прогнозы, особенно в долгосрочной перспективе. Поиск таких подходов стимулирует исследования в области квантовых вычислений и новых математических формализмов, нацеленных на повышение эффективности и точности моделирования сложных систем.

Формализм Купмана-Неймана (KvN) представляет собой новаторский подход к моделированию сложных классических систем, заключающийся во вложении их динамики в квантовомеханический формализм. Этот метод позволяет рассматривать классические переменные как операторы в гильбертовом пространстве, что открывает возможность применения квантовых алгоритмов для решения задач, неподдающихся классическому численному моделированию. В частности, KvN позволяет аппроксимировать нелинейную динамику линейными операторами, что упрощает вычисления и потенциально обеспечивает экспоненциальное ускорение по сравнению с традиционными методами. Исследования показывают, что данный подход может быть особенно полезен в таких областях, как гидродинамика и турбулентность, где долгосрочное прогнозирование остается сложной задачей, и, таким образом, открывает перспективы для достижения квантового преимущества в симуляции сложных систем и решении задач, требующих высокой вычислительной мощности.

Квантовое вложение: формализм Купмана-Неймана

Формализм КвН осуществляет отображение классического фазового пространства на гильбертово пространство, что позволяет применять инструменты квантовой механики для анализа классических систем. Данное преобразование предполагает, что каждая классическая функция, представляющая собой наблюдаемую, становится оператором в гильбертовом пространстве. Это отображение не является однозначным, но позволяет рассматривать эволюцию классических наблюдаемых как эволюцию квантовых операторов, описываемых унитарным оператором, соответствующим динамике классической системы. В результате, классические задачи могут быть сформулированы и решены с использованием квантово-механического аппарата, включая методы спектрального анализа и квантовых алгоритмов.

Оператор Купмана является линейным оператором, действующим на пространстве классических наблюдаемых и описывающим их эволюцию во времени в рамках классической динамической системы. Он преобразует функцию наблюдаемой $f(x)$ в $Uf(x)$, представляющую её значение в следующий момент времени. Спектральный анализ оператора Купмана позволяет выделить собственные значения и собственные векторы, что дает возможность разложить наблюдаемую на компоненты, эволюционирующие с определенными частотами. Это, в свою очередь, позволяет анализировать динамику системы в терминах этих частот и выявлять устойчивые и неустойчивые моды поведения, что является ключевым инструментом в анализе нелинейных систем и прогнозировании их поведения.

Преобразование, лежащее в основе формализма KvN, позволяет применять квантовые алгоритмы для решения классически сложных задач. В частности, продемонстрировано успешное применение данного подхода к решению уравнения Кортевега-де Вриса (KdV), известного своей нелинейностью и сложностью аналитического решения. Наши исследования показали возможность эффективного моделирования эволюции решений KdV с использованием квантовых вычислений, что открывает перспективы для квантового моделирования широкого класса сложных классических систем, ранее недоступных для точного численного анализа. Это достигается за счет представления классических наблюдаемых в виде операторов в гильбертовом пространстве и использования квантовых алгоритмов для вычисления их эволюции во времени.

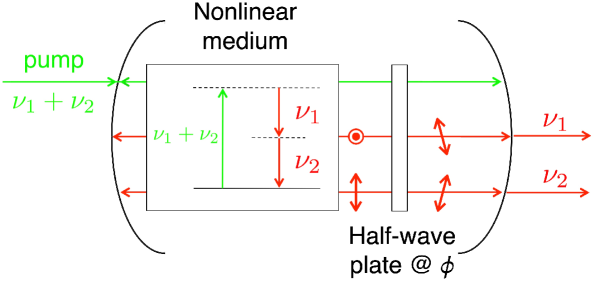
Реализация на основе непрерывно-переменных квантовых вычислений

Непрерывно-переменное квантовое вычисление (CVQC) предоставляет естественную платформу для реализации формализма KvN, используя фотонику для кодирования и манипулирования квантовыми состояниями. В CVQC информация кодируется в непрерывных степенях свободы квантовых состояний, таких как амплитуда и фаза электромагнитного поля. Фотоны, как носители квантовой информации, позволяют создавать и контролировать такие состояния с высокой точностью. В частности, кодирование информации в квадратурах электромагнитного поля — амплитуде $X$ и фазе $P$ — позволяет эффективно представлять квантовые операторы и состояния, упрощая реализацию квантовых алгоритмов и моделирование квантовых систем. Это позволяет избежать дискретизации, присущей кубитным системам, и обеспечивает более плавный переход к более сложным квантовым вычислениям.

Метод разложения Троттера-Сузуки позволяет аппроксимировать сложные операторы временной эволюции, возникающие в квантовых схемах. Данный подход основан на разложении экспоненты оператора, представляющего временную эволюцию, на произведение более простых операторов, которые могут быть эффективно реализованы последовательно. Математически, это выражается как $e^{-iHt}\approx {\prod }_{j=1}^n{e}^{-i{H}_{j}t/n}$, где $H$ — полный гамильтониан, а $H_j$ — его части, которые коммутируют друг с другом. Точность аппроксимации увеличивается с ростом числа членов $n$ в произведении, однако это также требует большего числа квантовых операций. Использование разложения Троттера-Сузуки является стандартным подходом в квантовом моделировании для решения задач, требующих эволюции квантового состояния во времени.

Для реализации непрерывно-переменных квантовых вычислений (CVQC) и, в частности, для аппроксимации оператора Купмана, ключевым является использование фотонных элементов. Разделители луча (beam splitters) и двухмодовые сжиматели (two-mode squeezers) позволяют создавать необходимые квантовые состояния, такие как сжатые состояния и запутанные фотоны. В нашей работе, успешная симуляция уравнения Кортевега-де Вриса (KdV) была достигнута именно за счет реализации оператора Купмана с использованием данных фотонных элементов, демонстрируя их функциональность и применимость в решении сложных дифференциальных уравнений. Настройка параметров данных элементов позволяет контролировать $\alpha$ и $\theta$ параметры сжатых состояний, необходимые для эффективного кодирования и манипулирования квантовой информацией.

Усиление производительности: передовые техники

Декогеренция, являющаяся одной из главных проблем в квантовых вычислениях, существенно снижает точность симуляций на основе квантовых $n$-частичных взаимодействий (KvN). Этот процесс, обусловленный взаимодействием квантовой системы с окружающей средой, приводит к потере квантовой информации и возникновению ошибок в вычислениях. Для компенсации негативного влияния декогеренции разрабатываются и внедряются различные стратегии смягчения ошибок. К ним относятся методы кванновой коррекции ошибок, динамическое подавление импульсов и оптимизация параметров квантовых схем. Эффективное противодействие декогеренции критически важно для реализации надежных и масштабируемых квантовых симуляторов и, в конечном итоге, для создания полноценных квантовых компьютеров.

Использование оптических гребенчатых источников позволяет значительно повысить точность и стабильность фотонных квантовых схем. Эти источники, генерирующие множество равноотстоящих друг от друга частот, обеспечивают прецизионное управление квантовыми битами, снижая влияние шумов и повышая когерентность системы. Благодаря этому, сложность и масштаб моделируемых квантовых систем возрастают, что критически важно для проведения высокоточных симуляций в таких областях, как квантовая химия и материаловедение. В частности, $\Delta \nu$ — ширина спектральной линии гребенки — напрямую влияет на точность представления квантовых состояний, позволяя более эффективно моделировать сложные квантовые явления и приближаясь к границе, где классические вычисления становятся невозможными.

Алгоритмы обучения с подкреплением демонстрируют значительный потенциал в оптимизации параметров квантовых вентилей и максимизации производительности реализаций КВК (непрерывно-переменной квантовой вычислительной техники). В отличие от традиционных методов, требующих ручной настройки или использования градиентных алгоритмов, обучение с подкреплением позволяет агенту самостоятельно исследовать пространство параметров, находя оптимальные конфигурации для конкретных квантовых схем. Этот подход особенно эффективен в условиях шума и несовершенства оборудования, где традиционные методы могут оказаться неэффективными. Используя вознаграждения, основанные на результатах симуляций или реальных измерений, алгоритм постепенно улучшает свои стратегии управления квантовыми вентилями, стремясь к минимизации ошибок и повышению точности вычислений. Исследования показывают, что обучение с подкреплением может существенно улучшить производительность КВК в задачах квантовой симуляции, оптимизации и машинного обучения, открывая новые возможности для развития квантовых технологий.

Перспективы: расширение масштабов моделирования

Формализм КвН, в сочетании с CVQC, представляет собой мощную основу для моделирования широкого спектра классических систем, начиная от динамики жидкостей и заканчивая прогнозированием погоды. Данный подход позволяет эффективно преобразовывать классические уравнения в квантовые аналоги, что открывает возможности для использования преимуществ квантовых вычислений. В частности, он обеспечивает более эффективное решение сложных дифференциальных уравнений, описывающих поведение жидкостей и газов, а также позволяет создавать более точные модели атмосферных процессов. Благодаря этому, появляется возможность значительно улучшить точность прогнозов погоды, оптимизировать процессы в химической промышленности и даже разработать новые материалы с заданными свойствами. Ключевым преимуществом является возможность моделирования систем, которые ранее были недоступны для классических вычислительных методов из-за их сложности и масштаба.

Дальнейшее развитие методов коррекции ошибок и оптимизации является ключевым для увеличения масштаба симуляций и решения более сложных задач. Эффективное подавление ошибок, возникающих в квантовых вычислениях, позволит значительно увеличить продолжительность и сложность моделируемых процессов, преодолевая текущие ограничения, связанные с декогеренцией и шумами. Одновременно, оптимизация алгоритмов и использование более эффективных методов представления данных позволит снизить вычислительные затраты и повысить скорость симуляций. Разработка новых алгоритмов коррекции ошибок, адаптированных к специфике KvN формализма и CVQC, а также применение методов машинного обучения для автоматической оптимизации параметров симуляций, откроют возможности для моделирования систем, которые ранее были недоступны, например, сложных турбулентных потоков или процессов в материалах с высокой степенью неоднородности. Успех в этой области позволит не только расширить горизонты научного познания, но и создать принципиально новые технологии в различных областях, от прогнозирования погоды до разработки новых материалов и лекарств.

Данный подход обладает потенциалом кардинально изменить понимание сложных систем и открыть возможности для создания инновационных технологий в различных областях. Успешное моделирование уравнения Кортевега-де Вриса является ярким примером, демонстрирующим перспективность метода и указывающим на возможность достижения квантового превосходства в решении задач, ранее недоступных для классических вычислений. Это открывает путь к разработке принципиально новых алгоритмов для моделирования турбулентности, прогнозирования погоды, оптимизации логистических процессов и даже к созданию более эффективных материалов с заданными свойствами. Использование комбинации формализма KvN и CVQC позволяет исследовать сложные взаимосвязи и нелинейные эффекты, которые лежат в основе многих природных явлений, предоставляя инструменты для более точного и глубокого анализа.

В этой работе пытаются применить изящную математику к фотонным кубитам. Koopman-von Neumann формализм — это, конечно, красиво, но всегда интересно, что из этого выйдет на практике. Авторы надеются ускорить симуляцию нелинейных систем, вроде уравнения Кортевега-де Вриса, перенеся её на квантовый компьютер с непрерывными переменными. Начинаешь подозревать, что сейчас это назовут квантовым ускорением и получат инвестиции. Как обычно, элегантная теория столкнётся с суровой реальностью троттеризации и шума. Как метко заметил Луи де Бройль: «Каждая «революционная» технология завтра станет техдолгом». И это абсолютно верно, ведь даже самое изящное решение рано или поздно обрастёт костылями и коммитами.

Что дальше?

Представленная работа, как и большинство попыток обуздать нелинейную динамику, неизбежно наталкивается на проблему масштабируемости. Преобразование классических уравнений, подобных уравнению Кортевега-де Вриса, в квантовые схемы — это лишь первый шаг. Реальное ускорение, обещанное квантовыми вычислениями, остаётся теоретическим, пока количество кубитов и сложность требуемых не-гауссовых гейтов не достигнут критической массы. И даже тогда, стоит помнить, что каждое «революционное» решение — это лишь новая форма технического долга.

Очевидным направлением дальнейших исследований является разработка более эффективных методов аппроксимации оператора Купмана-Неймана. Тротеризация, несмотря на свою простоту, в конечном итоге станет узким местом. Поиск альтернативных подходов, позволяющих снизить сложность квантовых схем без потери точности, представляется более перспективным, чем погоня за все большим количеством кубитов. Впрочем, история науки показывает, что элегантные решения часто оказываются неприменимыми в реальных условиях.

В конечном счёте, необходимо признать, что не всегда нужна очередная архитектура или новый алгоритм. Иногда требуется меньше иллюзий и больше понимания границ применимости существующих методов. Замена одного костыля другим — не прогресс, даже если он квантовый.

---

Оригинал статьи: https://arxiv.org/pdf/2512.13887.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/