Квантовые алгоритмы для машинного обучения: на пороге нового качества?

---

Новое исследование сравнивает эффективность квантовых машин опорных векторов и квантовых нейронных сетей с классическими подходами, демонстрируя потенциал для решения сложных задач.

Анализ производительности квантовых машин опорных векторов и квантовых нейронных сетей, реализованных с использованием фреймворков PennyLane и Qiskit.

Несмотря на успехи классических алгоритмов машинного обучения, задачи высокой сложности требуют новых подходов. В данной работе, посвященной ‘Performance Analysis of Quantum Support Vector Classifiers and Quantum Neural Networks’, проведено сравнительное исследование производительности квантовых классификаторов, включая квантовые машины опорных векторов и квантовые нейронные сети, в сравнении с их классическими аналогами. Полученные результаты свидетельствуют о том, что квантовые модели демонстрируют превосходство над классическими подходами по мере увеличения сложности решаемой задачи, особенно при использовании фреймворка Qiskit для оптимизации. Какие перспективы открывает дальнейшая разработка и оптимизация квантовых алгоритмов для решения задач машинного обучения в различных областях?

---

Традиционные и Квантовые Алгоритмы: Преодоление Границ Вычислений

Традиционные алгоритмы машинного обучения, несмотря на свою эффективность в решении широкого спектра задач, сталкиваются с серьезными ограничениями при работе с данными высокой размерности и сложностью. По мере увеличения числа признаков и взаимосвязей между ними, вычислительные затраты и время обучения экспоненциально возрастают, что делает анализ больших и сложных наборов данных практически невозможным. Это связано с тем, что классические алгоритмы оперируют битами, которые могут находиться только в одном состоянии — 0 или 1. В результате, для представления и обработки информации в многомерном пространстве требуется огромное количество вычислительных ресурсов, что создает «проклятие размерности» и ограничивает возможности классического машинного обучения в решении действительно сложных задач, требующих анализа больших объемов информации.

Квантовые вычисления представляют собой перспективное решение для задач, непосильных для классических алгоритмов, благодаря использованию уникальных квантовых явлений. В отличие от битов, хранящих информацию в виде 0 или 1, кубиты, фундаментальные единицы квантовой информации, могут находиться в состоянии суперпозиции, одновременно представляя и 0, и 1. Это позволяет квантовым компьютерам обрабатывать экспоненциально больше информации, чем классическим. Кроме того, явление квантовой запутанности позволяет кубитам быть коррелированными таким образом, что изменение состояния одного мгновенно влияет на состояние другого, независимо от расстояния. Такие свойства позволяют разрабатывать новые алгоритмы, способные эффективно решать сложные задачи оптимизации, моделирования и анализа данных, открывая новые горизонты в областях, требующих обработки огромных объемов информации, например, в химии, материаловедении и искусственном интеллекте.

Квантовое машинное обучение представляет собой перспективное направление, стремящееся к расширению и усовершенствованию существующих алгоритмов машинного обучения за счет использования преимуществ квантовых вычислений. Исследования показывают, что по мере увеличения сложности решаемых задач, квантовые модели демонстрируют сопоставимую, а в ряде случаев и превосходящую производительность по сравнению с классическими аналогами. Это достигается благодаря способности квантовых систем эффективно обрабатывать высокоразмерные данные и выполнять вычисления, недоступные для традиционных компьютеров. В частности, алгоритмы, использующие квантовую запутанность и суперпозицию, позволяют значительно ускорить процесс обучения и повысить точность прогнозов, открывая новые возможности в таких областях, как распознавание образов, анализ данных и оптимизация сложных систем.

Квантовое Кодирование Признаков: Преобразование Данных для Квантовых Схем

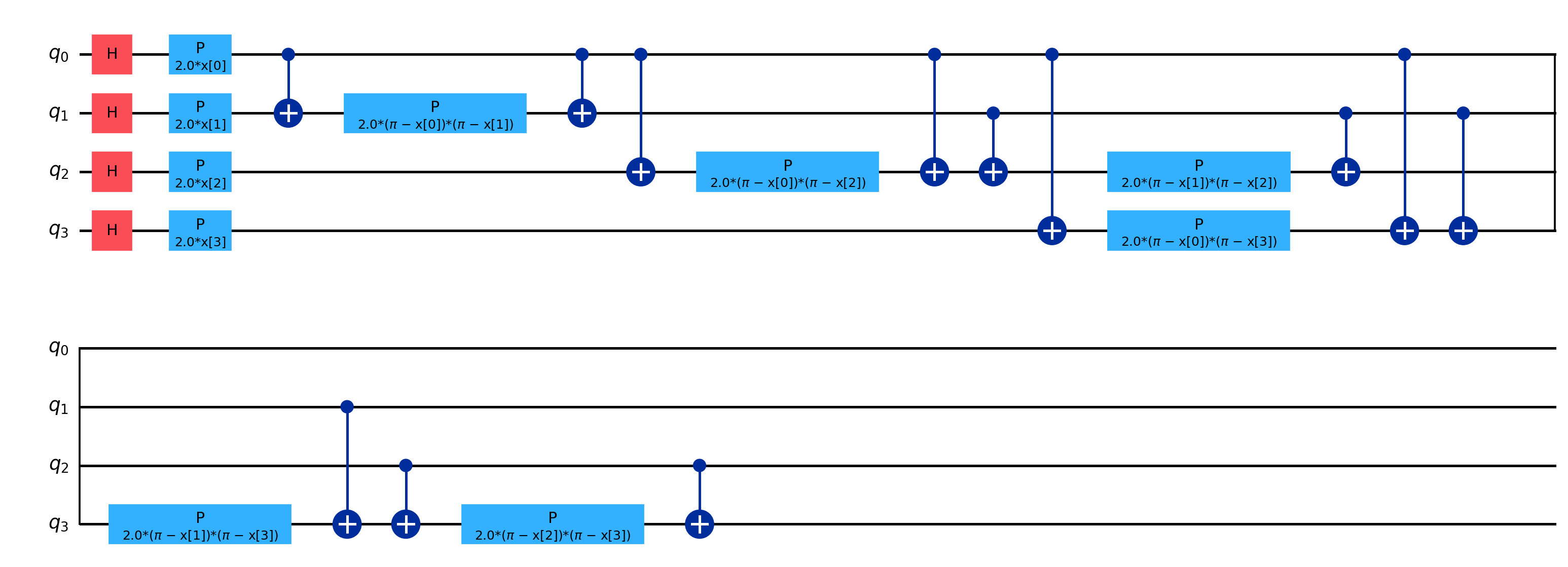
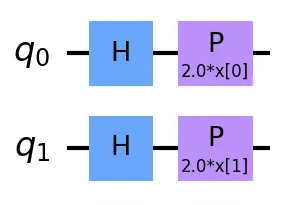
Квантовые отображения признаков, такие как ZFeatureMap и ZZFeatureMap, являются ключевым компонентом для преобразования классических данных в квантовые состояния, пригодные для обработки в квантовых схемах. Эти отображения выполняют кодирование данных путем применения последовательности квантовых вентилей к исходным данным, представляющим собой векторы вещественных чисел. В результате кодирования формируется квантовое состояние, которое представляет собой суперпозицию базовых состояний, отражающую закодированную информацию. Выбор конкретного отображения признаков напрямую влияет на структуру квантового состояния и, следовательно, на возможности квантовой модели в части извлечения закономерностей из данных и эффективности обучения. В процессе кодирования каждый элемент входного вектора данных отображается в амплитуду соответствующего базисного состояния квантовой системы.

Квантовые схемы кодирования данных используют базовые квантовые гейты, такие как фазовый сдвиг ($S$), гейт Адамара ($H$) и контролируемое НЕ ($CNOT$), для преобразования входных данных в высокоразмерное квантовое пространство признаков. Комбинация этих гейтов позволяет создавать сложные нелинейные преобразования, что потенциально позволяет модели выявлять и использовать более сложные взаимосвязи в данных, которые могут быть упущены линейными моделями. Эффективность кодирования напрямую зависит от выбора конкретной комбинации гейтов и порядка их применения, определяющих структуру и выразительность полученного пространства признаков.

Выбор карты признаков оказывает существенное влияние на выразительность и обучаемость результирующей квантовой модели. Выразительность, определяемая способностью модели аппроксимировать сложные функции, напрямую зависит от структуры и сложности выбранной карты признаков. Более сложные карты признаков, использующие больше квантовых вентилей и создающие пространства более высокой размерности, потенциально могут представлять более сложные зависимости в данных, но также могут потребовать больше ресурсов для обучения. Обучаемость, в свою очередь, характеризует скорость и эффективность процесса оптимизации параметров модели. Некоторые карты признаков могут приводить к проблемам, таким как затухание градиентов или плоские области в пространстве параметров, затрудняя обучение даже при достаточном количестве данных. Таким образом, оптимальный выбор карты признаков требует компромисса между выразительностью и обучаемостью, учитывая специфику решаемой задачи и доступные вычислительные ресурсы.

Вариационные Квантовые Схемы: Обучение Параметров в Квантовой Цепи

Вариационные квантовые схемы (ВКC) являются основой квантовых нейронных сетей (КНС), обеспечивая возможность обучения параметров непосредственно внутри квантовой цепи. ВКC состоят из последовательности квантовых вентилей, параметры которых ($\theta$) могут изменяться в процессе обучения. Обучение происходит путем оптимизации этих параметров для минимизации заданной функции потерь. В отличие от классических нейронных сетей с фиксированной архитектурой, ВКC позволяют гибко настраивать квантовую схему, что потенциально обеспечивает более эффективное представление данных и решение задач, недоступных для классических алгоритмов. Оптимизация параметров ВКC осуществляется с использованием классических алгоритмов оптимизации, таких как SPSA, что позволяет интегрировать квантовые вычисления с классической вычислительной инфраструктурой.

Обучение квантовых нейронных сетей (QNN) осуществляется посредством алгоритмов оптимизации, таких как SPSA (Simultaneous Perturbation Stochastic Approximation), направленных на минимизацию функции потерь. В качестве функции потерь часто используется CrossEntropyLoss, особенно при решении задач классификации. Процесс обучения заключается в итеративной корректировке параметров квантовой схемы с целью уменьшения значения функции потерь на обучающем наборе данных. Алгоритм SPSA, в отличие от градиентных методов, не требует вычисления градиента, что делает его применимым к квантовым схемам, для которых вычисление градиента может быть затруднительным или невозможным. Эффективность обучения оценивается по улучшению метрик производительности, таких как точность классификации или среднеквадратичная ошибка.

Для оценки производительности квантовых нейронных сетей (QNN) и сравнения их с классическими моделями используются стандартные наборы данных, такие как IrisDataset и MNISTPCA. В частности, при использовании вариационных квантовых схем (VQCs) на наборе данных IrisDataset достигнута точность в 92.33%. Эти наборы данных позволяют проводить количественную оценку эффективности QNN в задачах классификации и регрессии, обеспечивая основу для сравнения с традиционными алгоритмами машинного обучения и выявления потенциальных преимуществ квантовых вычислений в данной области.

Практические Аспекты и Будущие Направления Квантового Машинного Обучения

Подготовка данных играет первостепенную роль при обучении квантовых нейронных сетей (QNN). Нормализация данных, приводящая признаки к единому масштабу, предотвращает доминирование отдельных признаков и способствует более эффективному обучению модели. Разделение данных на обучающую и тестовую выборки, известное как TrainTestSplit, позволяет оценить способность модели к обобщению на новые, ранее не встречавшиеся данные. Без этих этапов предварительной обработки, QNN могут демонстрировать низкую производительность или нестабильность, даже при использовании самых современных квантовых алгоритмов. Тщательное применение методов нормализации, таких как масштабирование к диапазону $[0,1]$ или стандартизация с нулевым средним и единичным стандартным отклонением, в сочетании с корректным разделением данных, является необходимым условием для успешного обучения и оценки QNN.

Современные квантовые компьютеры функционируют в так называемую эпоху NISQ (Noisy Intermediate-Scale Quantum), что накладывает существенные ограничения на разработку и применение кванновых нейронных сетей (QNN). Ограниченное количество кубитов — порядка нескольких десятков или сотен — препятствует созданию достаточно сложных моделей, способных решать задачи, требующие высокой вычислительной мощности. Более того, неизбежный шум в квантовых операциях, вызванный несовершенством аппаратной реализации, вносит ошибки и искажения в вычисления, снижая точность и надежность QNN. Это требует разработки специальных алгоритмов и методов коррекции ошибок, а также адаптации архитектур QNN к условиям ограниченных ресурсов и высокой зашумленности, чтобы обеспечить практическую применимость квантовых вычислений в ближайшем будущем.

Разработка и внедрение квантовых нейронных сетей (QNN) значительно ускорилось благодаря специализированным фреймворкам, таким как PennyLane и Qiskit. Эти инструменты предоставляют исследователям и разработчикам необходимые ресурсы для создания, обучения и тестирования квантовых моделей. Результаты экспериментов демонстрируют потенциал QNN превосходить классические аналоги: на датасете MNIST-PCA квантовые модели показали повышение точности до 0.020 по сравнению с классическими подходами. Кроме того, вариационные квантовые схемы (VQCs) продемонстрировали улучшение на 0.074 по сравнению с квантовыми схемами с классическими весами (QSVCs) на том же наборе данных. Эти результаты подчеркивают растущую эффективность QNN и стимулируют дальнейшие исследования в области квантового машинного обучения, открывая новые перспективы для решения сложных вычислительных задач.

Исследование демонстрирует, что квантовые модели машинного обучения, такие как квантовые SVM и квантовые нейронные сети, способны достигать сопоставимой или превосходящей производительности по сравнению с классическими аналогами, особенно при увеличении сложности решаемых задач. Данный факт подтверждает стремление к созданию алгоритмов, чья корректность может быть доказана математически. Как однажды заметил Пол Дирак: «Я не понимаю, почему все так взволнованы квантовой механикой. Если бы я был богом, я бы создал мир, который можно было бы описать более простым способом». Эта фраза отражает идею о необходимости элегантности и математической чистоты в любой научной теории, включая и алгоритмы машинного обучения, реализованные с использованием Qiskit.

Куда Далее?

Представленные результаты, хотя и демонстрируют потенциал квантовых алгоритмов машинного обучения, не являются окончательным доказательством их превосходства. Напротив, они обнажают глубину нерешенных вопросов. Построение квантовых моделей, сопоставимых или превосходящих классические, — это не просто вопрос масштабирования кубитов, но и создание алгоритмических структур, обладающих внутренней математической элегантностью. Необходимо строго доказать, что наблюдаемые преимущества не являются артефактами конкретных наборов данных или реализации, а обусловлены фундаментальными свойствами квантовых вычислений.

Особое внимание следует уделить разработке квантовых ядер, способных эффективно отображать классические данные в квантовое пространство признаков. Текущие подходы часто полагаются на эвристические методы, лишенные математической строгости. Кроме того, выбор оптимальной вариационной схемы для квантовых нейронных сетей остается открытой проблемой. Наблюдаемое предпочтение Qiskit как платформы реализации, безусловно, заслуживает внимания, однако следует помнить, что удобство инструмента не заменяет фундаментальной корректности алгоритма.

В конечном счете, истинный прогресс в области квантового машинного обучения потребует не просто увеличения вычислительной мощности, а глубокого понимания взаимосвязи между квантовой механикой и математическими принципами обучения. Иначе, мы рискуем построить сложные, но в конечном итоге бессмысленные конструкции, лишенные внутренней непротиворечивости и предсказуемости.

---

Оригинал статьи: https://arxiv.org/pdf/2512.03094.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/