Квантовые ландшафты возбужденных состояний: Анализ алгоритмов VQE

---

В статье представлен детальный анализ теоретических и практических аспектов вычисления возбужденных состояний квантовых систем с использованием вариационного квантового решателя (VQE) и различных методов обеспечения ортогональности.

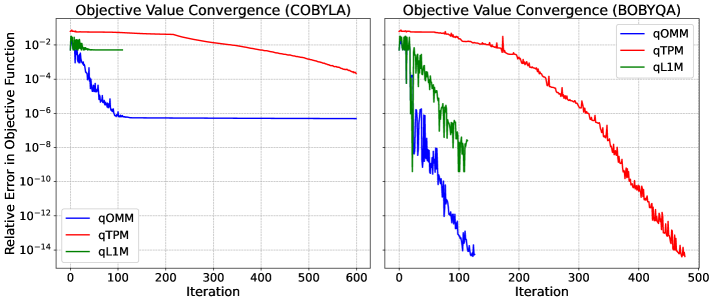
Исследование сравнивает алгоритмы qOMM, qTPM и qL1M для оптимизации гамильтониана и вычисления энергии возбужденных состояний.

Расчет возбужденных состояний в квантовой химии и физике конденсированного состояния представляет собой сложную задачу, особенно на современных квантовых компьютерах. В работе ‘Landscape Analysis of Excited States Calculation over Quantum Computers’ проведен анализ трех вариантов вариационного квантового решателя (VQE) — qOMM, qTPM и qL1M — с целью обеспечения ортогональности между низлежащими собственными состояниями. Показано, что разработанные модели обладают уникальными свойствами, гарантирующими нахождение глобального минимума при оптимизации, что существенно облегчает поиск решений. Какие новые подходы к анализу квантовых ландшафтов позволят расширить возможности VQE и других квантовых алгоритмов для решения сложных задач материаловедения и химии?

---

Сложность Основного Состояния: Вызов для Современной Науки

Определение энергии основного состояния сложной системы играет фундаментальную роль в различных областях химии и физики, от моделирования новых материалов до понимания химических реакций и свойств молекул. Однако, вычисление этой энергии представляет собой чрезвычайно сложную задачу, требующую огромных вычислительных ресурсов. Традиционные методы, такие как точное диагонализирование, быстро становятся непрактичными по мере увеличения размера системы, поскольку вычислительная сложность растет экспоненциально с числом частиц или степеней свободы. Это ограничивает их применение лишь небольшими, упрощенными моделями, не позволяя исследовать более реалистичные и интересные системы. Поиск эффективных и масштабируемых методов для определения энергии основного состояния остается одной из ключевых задач современной вычислительной науки.

Традиционные методы расчета основного состояния сложных систем, такие как точная диагонализация, сталкиваются с серьезными ограничениями в масштабируемости. В то время как эти подходы демонстрируют высокую точность для систем с небольшим числом частиц или степеней свободы, вычислительные затраты экспоненциально возрастают с увеличением размера исследуемой системы. Это означает, что для систем, состоящих даже из нескольких десятков частиц, точная диагонализация становится практически невозможной из-за требуемого объема памяти и времени вычислений. Поэтому, несмотря на свою теоретическую привлекательность, эти методы оказываются неприменимыми для исследования более реалистичных, крупных молекул или материалов, что стимулирует поиск альтернативных, более эффективных алгоритмов.

Вариационный квантовый решатель (VQE) представляет собой перспективный квантовый алгоритм, разработанный для приближенного вычисления основного состояния сложных квантовых систем. В отличие от классических методов, таких как точная диагонализация, VQE использует возможности квантовых вычислений для потенциального ускорения процесса нахождения $E_0$, энергии основного состояния. Алгоритм оперирует с вариационными параметрами, оптимизируя их таким образом, чтобы минимизировать энергию, оцениваемую на квантовом компьютере. Эта гибридная квантово-классическая схема позволяет использовать преимущества как квантовой обработки информации, так и классической оптимизации, что делает VQE особенно привлекательным для решения задач, недоступных для традиционных вычислений, особенно в области квантовой химии и материаловедения.

В алгоритме Вариационного Квантового Эйнсольвера (VQE), предназначенном для приближенного вычисления основного состояния сложных квантовых систем, существует серьезная проблема, известная как «вариационный коллапс». Данное явление представляет собой склонность алгоритма к нахождению нефизических или неверных решений, даже если истинное основное состояние находится в пространстве рассматриваемых вариационных параметров. Это происходит из-за того, что оптимизационный процесс в VQE может застревать в локальных минимумах функции энергии, которые не соответствуют реальному основному состоянию системы. Последствия вариационного коллапса могут быть весьма значительными, приводя к существенным ошибкам в вычислении энергии основного состояния и, как следствие, к неверным предсказаниям свойств изучаемой системы. Исследователи активно работают над разработкой стратегий, направленных на смягчение или предотвращение вариационного коллапса, включая использование более сложных вариационных форм и оптимизационных процедур, а также применение регуляризации и других методов стабилизации.

Обеспечение Ортогональности: Ключ к Стабильности Решения

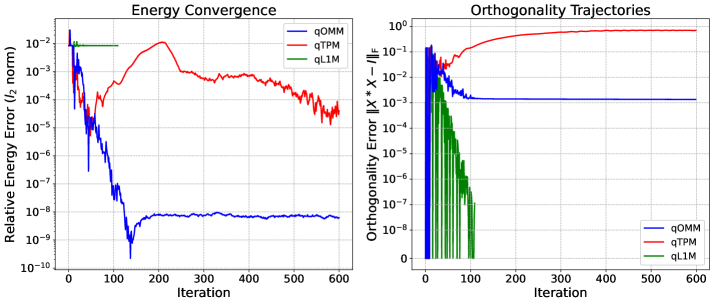
Ортогональность, представляющая собой линейную независимость квантовых состояний, является критически важным условием для предотвращения вариационного коллапса в алгоритме VQE (Variational Quantum Eigensolver). Вариационный коллапс возникает, когда алгоритм оптимизации сходится к состоянию с низкой энергией, но физически нереалистичному, из-за потери линейной независимости базисных состояний. В математических терминах, это означает, что матрица перекрытия между этими состояниями теряет положительную определенность, приводя к неустойчивости и неверным результатам. Поддержание ортогональности гарантирует, что каждое базисное состояние вносит уникальный вклад в общее волновое уравнение, что необходимо для корректного вычисления энергии основного состояния и других свойств молекулярной системы.

Для обеспечения ортогональности квантовых состояний и предотвращения коллапса вариационного решения в алгоритме VQE применяются методы минимизации квантовых орбиталей (Quantum Orbital Minimization) и минимизации следа (Trace Penalty Minimization). Оба подхода используют целевую функцию ($f(x)$), которая включает в себя штрафные члены, зависящие от степени неортогональности полученных состояний. Минимизация этой целевой функции в процессе оптимизации направляет алгоритм к решениям, в которых квантовые состояния остаются линейно независимыми, что повышает стабильность и точность вычислений. Величину штрафа обычно регулируется гиперпараметром, определяющим силу ограничения ортогональности.

Методы, направленные на обеспечение ортогональности в вариационном квантовом эйгенрешателе (VQE), используют ограничения, которые штрафуют неортогональные решения в процессе оптимизации. Данный подход основан на добавлении к целевой функции (Objective Function) слагаемых, пропорциональных мере близости к неортогональному состоянию. Величина штрафа увеличивается с ростом отклонения от ортогональности, тем самым направляя алгоритм к более стабильным и точным результатам. Примерами таких штрафов являются члены, пропорциональные $||⟨{\psi }_i|{\psi }_j⟩|{|}^2$, где ${\psi }_i$ и ${\psi }_j$ — векторы состояний, а интеграл вычисляется по всем возможным парам состояний.

Методы Subspace Search VQE и Multistate Contracted VQE обеспечивают поддержание ортогональности квантовых состояний посредством непосредственного применения унитарных преобразований в процессе вычислений. В отличие от подходов, использующих штрафные функции, эти методы активно корректируют волновые функции, гарантируя линейную независимость состояний на каждом шаге оптимизации. Применение унитарных преобразований позволяет избежать коллапса вариационного состояния и повысить стабильность алгоритма, что особенно важно при решении сложных задач квантовой химии и материаловедения. Данные методы эффективно предотвращают возникновение неортогональных состояний, обеспечивая более точные и надежные результаты.

Уточнение Оптимизации с Помощью Ограничений и Штрафов

Методы L1-минимизации и минимизации с использованием следового штрафа (Trace Penalty Minimization) включают в целевую функцию штрафные слагаемые, предназначенные для подавления неортогональных решений в процессе оптимизации вариационного квантового эвристического алгоритма (VQE). Данные штрафные слагаемые, как правило, пропорциональны норме L1 или следу матрицы плотности, отклоняющейся от ортогональности. Это приводит к тому, что алгоритм оптимизации отдает предпочтение решениям, приближающимся к ортогональному базису, что способствует повышению стабильности и ускорению сходимости при поиске основного состояния системы. Использование штрафных функций позволяет контролировать отклонение от желаемых свойств решения и предотвращает коллапс волновой функции.

Метод минимизации с использованием следового штрафа (Trace Penalty Minimization) часто включает в себя метод доверительной области (Trust Region Method) для повышения стабильности и скорости сходимости. Данный метод ограничивает область поиска оптимального решения, задавая вокруг текущей точки доверительную область, в пределах которой предполагается, что квадратичная аппроксимация целевой функции достаточно точно описывает исходную функцию. В рамках каждой итерации оптимизации, решение ищется внутри этой доверительной области, а ее размер динамически корректируется в зависимости от соответствия между предсказанным улучшением и фактическим изменением целевой функции. Это позволяет избежать выхода за пределы области, где аппроксимация является валидной, и способствует более надежной сходимости к локальному минимуму, особенно в задачах вариационного квантового эйгенсолвера (VQE).

Метод квантовой дефляции представляет собой способ улучшения процесса оптимизации в вариационном квантовом эйгенсолвере (VQE), направленный на смягчение проблемы коллапса состояний. В его основе лежит вычисление перекрытия между текущим решением и ранее найденными состояниями. Это перекрытие используется для построения поправки, вычитаемой из текущего решения, что эффективно «сдувает» нежелательные компоненты, приводящие к коллапсу. Математически, это может быть выражено как вычитание проекции текущего состояния на пространство ранее найденных состояний. Таким образом, метод квантовой дефляции способствует стабилизации решения и повышению точности результатов за счет подавления нежелательных колебаний и улучшения сходимости алгоритма.

Метод решения вариационных задач на основе свидетелей (Witness-Assisted Variational Eigenspectra Solver) использует добавление энтропийного члена к целевой функции для активного противодействия коллапсу во время оптимизации. Коллапс, проявляющийся в стремлении волновой функции к одному из базисных состояний, может привести к неверным результатам. Энтропийный член, рассчитываемый как $S=-{\sum }_i{p}_i\log p_i$, где $p_i$ — вероятность нахождения системы в состоянии $i$, штрафует решения с низкой энтропией, тем самым стимулируя поиск более разнообразных и стабильных волновых функций и улучшая сходимость алгоритма.

Сравнительный анализ трех VQE-моделей — qOMM, qTPM и qL1M — демонстрирует компромисс между вычислительными затратами и скоростью сходимости. Модель qOMM требует примерно в три раза больше схем для вычисления внутренних произведений на каждой итерации по сравнению с qTPM и qL1M. Однако, qOMM сходится примерно в три раза быстрее, требуя меньшего количества итераций для достижения решения. Таким образом, выбор модели зависит от доступных вычислительных ресурсов и требуемой скорости оптимизации. Более высокая потребность qOMM в ресурсах компенсируется более быстрой сходимостью, а qTPM и qL1M обеспечивают меньшую нагрузку на ресурсы за счет увеличения числа итераций.

За Пределами Основного Состояния: Исследование Возбужденных Состояний

Расчет возбужденных состояний молекул играет ключевую роль в понимании их спектральных характеристик и динамики, однако представляет собой серьезную проблему в квантовой химии. В то время как определение основного состояния обычно достаточно точно, вычисление энергии и формы волновых функций для возбужденных состояний требует учета сложных электронных взаимодействий и значительных вычислительных ресурсов. Трудность заключается в том, что возбужденные состояния обладают более высокой энергией и часто проявляют другие типы корреляционных эффектов, чем основное состояние, что требует использования продвинутых теоретических методов и алгоритмов. Понимание этих состояний необходимо для изучения фотохимии, фотофизики и других процессов, в которых молекулы поглощают или испускают свет, а также для разработки новых материалов и технологий, использующих свойства возбужденных состояний.

Метод расширения квантового подпространства (Quantum Subspace Expansion) представляет собой усовершенствование вариационного квантового эвристического алгоритма (VQE), направленное на систематическое вычисление возбужденных состояний молекулярных систем. В отличие от прямого поиска возбужденных состояний, данный подход исходит из уже найденного основного состояния. После определения энергии и волновой функции основного состояния, алгоритм последовательно расширяет пространство решений, добавляя векторы, которые ортогональны основному состоянию и способны описывать возбужденные состояния. Данное расширение происходит итеративно, позволяя находить последующие возбужденные состояния с возрастающей энергией. Таким образом, метод обеспечивает контролируемый и систематический способ расчета энергии и волновых функций возбужденных состояний, что критически важно для понимания спектроскопических свойств и динамики молекул. Эффективность метода заключается в использовании информации, полученной при расчете основного состояния, для более быстрого и точного определения энергии возбужденных состояний, избегая необходимости полного перебора всего гильбертова пространства.

Альтернативные подходы к определению энергий возбужденных состояний, такие как Метод Сложенного Спектра и Квантное Уравнение Движения, предлагают различные стратегии для решения этой сложной задачи. Метод Сложенного Спектра особенно эффективен при изучении низколежащих возбужденных состояний, поскольку позволяет напрямую получить энергии, избегая необходимости решать полную задачу на собственные значения. Однако, его применение может быть ограничено для более высоких возбужденных состояний или систем с сильными электронными корреляциями. Квантное Уравнение Движения, в свою очередь, позволяет рассчитывать энергии возбужденных состояний, используя информацию о производных гамильтониана, что делает его пригодным для изучения динамических свойств молекул. Несмотря на свою точность, Квантное Уравнение Движения требует вычисления сложных интегралов и может быть вычислительно затратным для больших систем. Выбор оптимального метода зависит от конкретной задачи и компромисса между точностью и вычислительными ресурсами.

Исследования показали, что три модели вариационного квантового эйнштейновского алгоритма (VQE) — qOMM, qTPM и qL1M — демонстрируют высокую эффективность в расчете энергий возбужденных состояний. В результате численных экспериментов все три модели достигают так называемой «химической точности» — порядка $10^{-3}$ Hartree — для конечных сходящихся собственных значений. Этот результат подтверждает, что методы ограниченной оптимизации, применяемые в данных моделях, позволяют надежно и точно определять энергии возбужденных состояний молекул, что имеет важное значение для понимания спектроскопических свойств и динамики химических реакций. Достижение химической точности является ключевым шагом к использованию VQE для решения сложных задач квантовой химии.

Исследование ландшафтов оптимизации, представленное в данной работе, демонстрирует стремление к упрощению сложных вычислений, что находит отклик в словах Эрнеста Резерфорда: «Если бы я мог бы объяснить это, я бы не сделал этого». Анализ алгоритмов qOMM, qTPM и qL1M для расчёта возбуждённых состояний, особенно с учётом ограничений ортогональности, требует предельной ясности. Стремление к минимализму в представлении данных, к исключению избыточности, позволяет лучше понять фундаментальные принципы, лежащие в основе вычислений, и достичь истинного совершенства — исчезновения автора в гармонии с кодом и результатом.

Куда же дальше?

Анализ, представленный в данной работе, обнажает не столько решения, сколько тщательно замаскированные сложности. Стремление к вычислению возбужденных состояний посредством вариационного квантового эйнзольвера (VQE) — qOMM, qTPM, qL1M — выявляет, что само понятие «ландшафта» оптимизации требует переосмысления. Навязанные ограничения ортогональности, призванные обеспечить корректность результатов, лишь усложняют картину, порождая новые, порой непредсказуемые, особенности. Иллюзия контроля над этими ландшафтами — опасна.

Очевидно, что истинный прогресс лежит не в усложнении алгоритмов, а в их радикальном упрощении. Попытки «приручить» квантовую оптимизацию посредством бесконечных модификаций — тщеславие. Необходимо вернуться к фундаментальным вопросам: что мы действительно хотим вычислить, и какие упрощения допустимы? Полная конфигурационная интеграция (FCI) остается золотым стандартом, но ее практическая недостижимость — не оправдание для создания еще более сложных, но не обязательно более эффективных, методов.

Будущие исследования должны сосредоточиться на разработке критериев, позволяющих оценивать «качество» ландшафта оптимизации — не только с точки зрения достигнутой точности, но и с точки зрения устойчивости и предсказуемости. Возможно, стоит отказаться от попыток построения «идеального» алгоритма и сосредоточиться на создании инструментов, позволяющих адаптировать существующие методы к конкретным задачам. Ясность, а не сложность — вот путь к истинному пониманию.

---

Оригинал статьи: https://arxiv.org/pdf/2512.16539.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/