Искусственный интеллект
Квантовые нейросети на волнах света: новый подход к обучению
Автор: Денис Аветисян
Исследователи предложили архитектуру квантовой нейронной сети, использующей непрерывные переменные и вдохновленную принципами квантовой оптики, для повышения эффективности и анализируемости.

В работе представлена квантовая нейронная сеть с непрерывными переменными (CV-QONN), обладающая аналитически отслеживаемой не-гауссовостью и демонстрирующая перспективные результаты в эталонных задачах.
Несмотря на перспективность квантовых вычислений, создание практически реализуемых квантовых нейронных сетей остается сложной задачей. В статье ‘Hardware-inspired Continuous Variables Quantum Optical Neural Networks’ представлена новая архитектура квантовой оптической нейронной сети непрерывных переменных (CV-QONN), использующая доступные фотонные компоненты и аналитически отслеживаемую не-гауссовость. Разработанная модель демонстрирует соответствие теореме универсальной аппроксимации и позволяет эффективно симулировать обучение сети с помощью библиотеки QuaNNTO, основанной на расширении Вика-Иссерлиса и преобразованиях Боголюбова. Способна ли данная архитектура стать основой для масштабируемого фотонного квантового машинного обучения и решения сложных задач квантовой обработки информации?
Непрерывные переменные: Новый рубеж квантового машинного обучения
Традиционные алгоритмы машинного обучения, как правило, оптимизированы для работы с дискретными данными, представленными в виде отдельных категорий или значений. Однако, значительная часть реальных физических систем характеризуется непрерывными переменными, такими как температура, давление или фаза волны. Эти системы описываются непрерывными функциями и требуют иных подходов к моделированию. Например, в квантовой механике, состояние частицы описывается непрерывным волновым уравнением. Использование дискретных методов для анализа таких систем приводит к упрощениям и потере информации, снижая точность прогнозов и ограничивая возможности для глубокого понимания процессов. Поэтому, разработка методов машинного обучения, способных эффективно обрабатывать непрерывные данные, является ключевой задачей для расширения возможностей анализа и моделирования в различных областях науки и техники.
Квантовые вычисления, использующие непрерывные степени свободы, представляют собой естественное соответствие для моделирования множества физических систем, что обещает значительные преимущества по сравнению с классическими подходами. В отличие от дискретных битов, лежащих в основе традиционных квантовых алгоритмов, непрерывные переменные, такие как амплитуда и фаза электромагнитного поля, позволяют более точно и эффективно описывать аналоговые данные, встречающиеся в реальном мире. Это особенно важно для задач, связанных с обработкой сигналов, моделированием квантовой динамики и решением дифференциальных уравнений. Использование непрерывных переменных открывает возможности для создания квантовых алгоритмов, которые могут превзойти классические аналоги в скорости и точности, а также позволяют исследовать новые подходы к машинному обучению, адаптированные к природе квантовых данных и процессов.
Подход, известный как «Непрерывные переменные» (), представляет собой мощную альтернативу традиционным квантовым вычислениям, основанным на кубитах. Вместо дискретных битов информации, он использует непрерывные степени свободы, такие как фаза и амплитуда света, для кодирования и обработки данных. Это открывает принципиально новые возможности для разработки квантовых алгоритмов, особенно в задачах, связанных с моделированием физических систем, где переменные по своей природе являются непрерывными. В отличие от кубитных алгоритмов, требующих точного управления отдельными кубитами, алгоритмы на основе непрерывных переменных могут использовать преимущества, связанные с естественным представлением непрерывных данных, что потенциально приводит к более эффективным и устойчивым вычислениям. Разработка новых алгоритмов и архитектур, использующих этот подход, позволяет исследовать области, ранее недоступные для кубитных систем, и расширяет границы квантовых вычислений.
Для полной реализации потенциала квантового машинного обучения с использованием непрерывных переменных, необходимы архитектуры, способные эффективно использовать нелинейность. В то время как линейные схемы могут обрабатывать определенные типы данных, большинство реальных физических систем демонстрируют нелинейное поведение, что требует нелинейных операций для точного моделирования. Текущие реализации, однако, часто сталкиваются с трудностями в создании и поддержании достаточной нелинейности, что ограничивает сложность задач, которые они могут эффективно решать. Преодоление этого ограничения требует разработки новых материалов, схем и методов управления, которые позволят создавать стабильные и масштабируемые нелинейные квантовые цепи. Достижение этой цели откроет путь к более мощным и универсальным алгоритмам квантового машинного обучения, способным решать задачи, недоступные для классических или линейных квантовых подходов.

Негауссовость как ключ к квантовому превосходству
Гауссовы состояния, несмотря на простоту подготовки и манипулирования ими, обладают ограниченной выразительностью, недостаточной для реализации универсальных квантовых вычислений. Это связано с тем, что гауссовы операции линейны и не могут генерировать все возможные квантовые состояния. В частности, гауссовы состояния не способны эффективно представлять состояния, необходимые для некоторых ключевых квантовых алгоритмов, таких как алгоритмы факторизации или квантового моделирования. В результате, для достижения квантового превосходства и реализации универсальных квантовых вычислений требуется использование не-гауссовых состояний и операций, способных преодолеть эти ограничения и обеспечить более широкий спектр квантовых возможностей.
Негауссовы ресурсы, такие как вычитание фотона (), являются ключевыми для введения нелинейности в квантовые схемы и реализации более сложных квантовых алгоритмов. Гауссовы состояния, несмотря на простоту подготовки и манипулирования, ограничены в выразительности и не способны к универсальным квантовым вычислениям. Операции, генерирующие негауссовы состояния, позволяют выходить за рамки гауссовой модели, создавая запутанные состояния с повышенной вычислительной мощностью. В частности, вычитание фотона подразумевает детектирование одного фотона в квантовом состоянии, что приводит к созданию неклассического состояния, необходимого для выполнения задач, недоступных классическим компьютерам.
Операции, вводящие негауссовость, такие как вычитание фотона, преодолевают ограничения, присущие гауссовским моделям, позволяя создавать запутанные состояния с повышенной вычислительной мощностью. Гауссовские состояния, хотя и удобны для подготовки и манипулирования, не способны обеспечить универсальность квантовых вычислений. Введение нелинейности посредством негауссовых ресурсов приводит к созданию состояний, не описываемых гауссовским распределением, и, как следствие, к возможности реализации квантовых алгоритмов, превосходящих классические аналоги. Эти состояния характеризуются корреляциями, которые не могут быть воспроизведены с использованием только гауссовских ресурсов, что является ключевым фактором для достижения квантового превосходства в различных вычислительных задачах, включая, например, обработку информации и моделирование сложных систем.
Тщательно разработанные неГауссовы ресурсы позволяют добиться ускорения квантовых вычислений в задачах машинного обучения. В частности, использование таких ресурсов, как вычитание фотонов или сжатые состояния, создает нелинейности, необходимые для реализации квантовых алгоритмов, превосходящих классические аналоги. Эти неГауссовы состояния позволяют эффективно кодировать и обрабатывать данные, что приводит к экспоненциальному ускорению определенных алгоритмов машинного обучения, например, в задачах классификации, регрессии и кластеризации. Применение неГауссовых ресурсов позволяет решать сложные задачи оптимизации и анализа данных, которые недоступны для классических вычислительных систем, открывая новые возможности в области искусственного интеллекта и анализа больших данных.
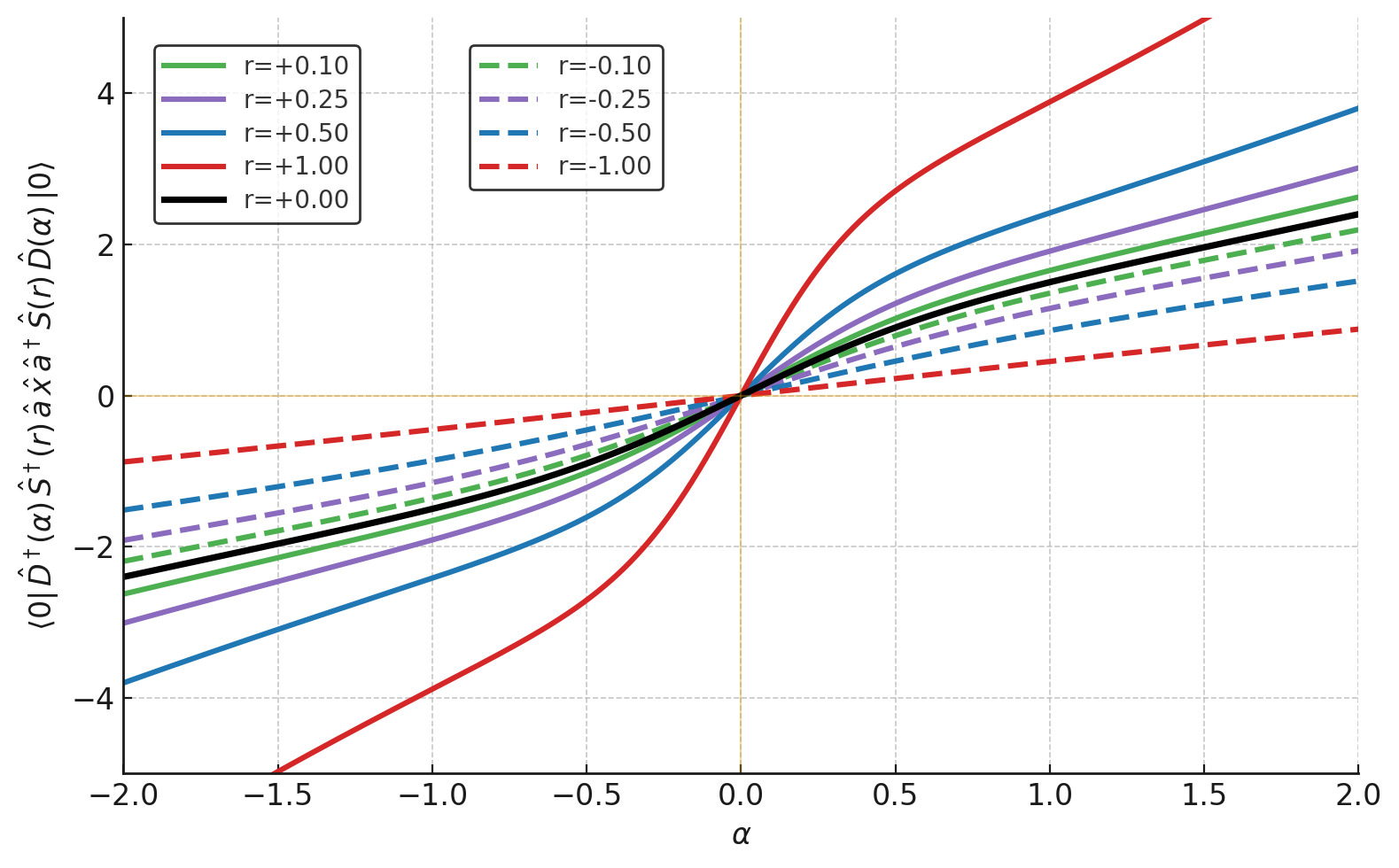
NN-modeQONN: Квантовая нейронная сеть с непрерывными переменными
Предлагаемая архитектура представляет собой новый подход к квантовым нейронным сетям, основанный на вычислениях с непрерывными переменными (Continuous-Variable, CV). В отличие от традиционных квантовых нейронных сетей, использующих кубиты, оперирует с квантовыми состояниями, описываемыми непрерывными амплитудами, что позволяет использовать преимущества CV-квантовых вычислений, такие как более простое аппаратное обеспечение и более высокая устойчивость к ошибкам. Данная архитектура использует квантовые состояния, представленные векторами в гильбертовом пространстве, и манипулирует ими посредством унитарных преобразований, что обеспечивает возможность обучения и решения сложных задач машинного обучения.
В архитектуре для создания высокоэкспрессивной и обучаемой модели используются преобразования в сочетании с вычитанием фотонов (Photon Subtraction). преобразования обеспечивают эффективное манипулирование квантовыми состояниями, представляя собой линейные преобразования когерентных состояний. Вычитание фотонов, в свою очередь, вводит нелинейность в модель, расширяя ее возможности представления и позволяя аппроксимировать более сложные функции. Комбинация этих двух операций позволяет эффективно моделировать сложные зависимости в данных и адаптироваться к различным задачам машинного обучения.
Сеть NN-modeQONN использует преобразования Боголюбова () и теорему Вика-Иссерлиса (Wick’s\ theorem) для эффективного вычисления математических ожиданий, что является критически важным для масштабируемого обучения. Преобразования Боголюбова позволяют выразить операторы создания и уничтожения в новом базисе, упрощая вычисление корреляционных функций. Теорема Вика-Иссерлиса, в свою очередь, позволяет разложить математическое ожидание произведения операторов на сумму произведений двухточечных корреляций, что существенно снижает вычислительную сложность. Такой подход позволяет избежать экспоненциального роста вычислительных затрат при увеличении числа кубитов и, следовательно, обеспечивает возможность обучения более сложных и мощных квантовых нейронных сетей.
Для эффективной обработки и анализа квантовой информации в архитектуре NN-modeQONN используется операция смещения () и гомодинное детектирование (). Операция смещения позволяет модулировать квантовое состояние, добавляя когерентное возбуждение, что расширяет возможности представления данных. Гомодинное детектирование, измеряющее квадратуры электромагнитного поля, предоставляет информацию о состоянии квантового сигнала. Комбинация этих двух методов позволяет эффективно преобразовывать квантовую информацию в классические данные, пригодные для дальнейшей обработки и обучения нейронной сети. Использование гомодинного детектирования, в частности, позволяет получать непрерывные значения, что упрощает процесс оптимизации параметров сети.

Валидация и масштабируемость посредством классического моделирования
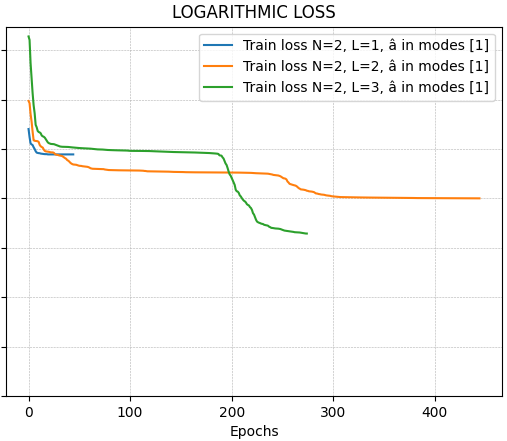
Нейронная сеть была обучена на специально подготовленном наборе данных , что позволило ей приобрести способность к эффективному решению сложных задач. Процесс обучения осуществлялся посредством минимизации разработанной , которая выступала в качестве критерия оценки качества работы сети. Данный подход позволил добиться высокой точности и стабильности результатов, поскольку нацелена на снижение расхождений между предсказаниями сети и ожидаемыми значениями. В результате, демонстрирует способность к обобщению и адаптации к новым данным, что делает ее перспективным инструментом для различных приложений, требующих анализа и распознавания сложных закономерностей.
Классическое моделирование, использующее методы , предоставило важный инструмент для проверки и усовершенствования поведения разработанной нейронной сети. Данный подход позволил тщательно протестировать алгоритмы и архитектуру сети в контролируемой среде, до ее реализации на квантовом оборудовании. Благодаря классическим симуляциям стало возможным выявить и устранить потенциальные ошибки, оптимизировать параметры обучения и оценить общую производительность системы. Такой способ проверки гарантирует надежность и точность результатов, полученных с помощью , и служит основой для дальнейшего масштабирования и применения в более сложных задачах анализа данных и распознавания образов.
Исследования показали, что разработанная нейронная сеть способна эффективно осваивать сложные функциональные зависимости, демонстрируя значительный потенциал в задачах распознавания образов и анализа данных. Применяемый подход обеспечивает существенный прирост скорости моделирования по сравнению с традиционными симуляторами, основанными на представлении в пространстве Фока, благодаря избежанию необходимости усечения пространства Гильберта. Это позволяет обрабатывать более сложные задачи и получать результаты с повышенной точностью, открывая новые возможности для применения в различных областях науки и техники, где требуется анализ больших объемов данных и выявление скрытых закономерностей.
Проведенное моделирование не только подтверждает эффективность разработанной нейронной сети, но и создает прочную основу для ее реализации на реальном квантовом оборудовании, открывая новые перспективы в области квантового машинного обучения. Достигнута высокая точность синтеза сложных не-гауссовых квантовых вентилей благодаря точному сопоставлению статистических моментов, а также получена практически нулевая ошибка при аппроксимации с использованием однослойных квантовых нейронных сетей, что подтверждает универсальность апроксимации (Universal Approximation Theorem — UAT). Данные результаты свидетельствуют о потенциале разработанного подхода для решения сложных вычислительных задач, недоступных классическим алгоритмам, и приближают эру практического квантового машинного обучения.
Исследование, представленное в данной работе, демонстрирует стремление к проверке границ существующих представлений о квантовых нейронных сетях. Архитектура CV-QONN, основанная на аналитически управляемой не-гауссовости, представляет собой вызов традиционным подходам. Как заметил Ричард Фейнман: «Я не могу воспроизвести реальность, я могу только изучать её». Данная работа, используя теорему Вика-Иссерлиса и преобразование Боголюбова, не просто моделирует квантовые процессы, но и исследует возможности их контролируемого нарушения для достижения лучших результатов в задачах машинного обучения. Изучение не-гауссовости, как ключевого аспекта, позволяет понять, как далеко можно зайти в использовании квантовых преимуществ.
Что дальше?
Представленная архитектура CV-QONN, хотя и демонстрирует анализируемую не-гауссовость — полезную особенность для классического моделирования — лишь приоткрывает дверь в мир квантовых нейронных сетей непрерывных переменных. Реальность, как открытый исходный код, требует не просто чтения, но и перекомпиляции. Использование теоремы Вика-Иссерлиса — элегантный, но всё же приближённый метод. Неизбежно встаёт вопрос о масштабируемости: сможет ли эта архитектура удержать сложность реальных задач, не превратившись в неуправляемый клубок преобразований Боголюбова?
Ограничения текущего подхода очевидны. Поиск оптимальных параметров сети, даже в рамках аналитически разрешимой модели, остаётся нетривиальной задачей. Более того, зависимость от конкретных задач-бенчмарков не позволяет судить об универсальности предложенного подхода. Следующим шагом видится разработка методов, позволяющих эффективно исследовать пространство параметров и адаптировать архитектуру к различным типам данных.
В конечном счёте, настоящая проверка ждёт впереди — в столкновении с задачами, которые принципиально неразрешимы для классических алгоритмов. Истинная сила квантовых нейронных сетей заключается не в имитации классических, а в создании принципиально нового способа обработки информации. Это не просто вопрос оптимизации, а переосмысления самой концепции вычислений.
Оригинал статьи: https://arxiv.org/pdf/2512.05204.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Статья также опубликована на личном сайте автора.