Квантовые схемы: новый взгляд на трансляцию с помощью нейросетей

---

Исследователи продемонстрировали, что модели на основе архитектуры Transformer способны эффективно преобразовывать квантовые схемы между различными аппаратными платформами.

Алгоритм, основанный на Transformer, обеспечивает точность трансляции квантовых схем между IBM и IonQ более 99,98%, открывая возможности для оптимизации квантовых вычислений.

Несмотря на значительный прогресс в области квантовых вычислений, эффективная трансляция квантовых схем между различными аппаратными платформами остается сложной задачей. В статье ‘Transpiling quantum circuits by a transformers-based algorithm’ предложен новый подход, использующий архитектуру Transformer для автоматической трансляции квантовых схем из стандартного QASM в наборы инструкций, оптимизированные для конкретного квантового оборудования, в частности, ионных ловушек IonQ. Показано, что разработанная модель обеспечивает точность трансляции более 99.98% для схем до пяти кубитов, при этом сложность модели масштабируется полиномиально с увеличением глубины схемы и числа гейтов. Возможно ли дальнейшее масштабирование данного подхода для решения задач оптимизации квантовых вычислений на более крупных и сложных системах?

---

Квантовые схемы: проблема перевода с одного железа на другое

Квантовые вычисления, обещающие революционные изменения в различных областях науки и техники, сталкиваются с существенной проблемой реализации. Полная реализация потенциала этих вычислений напрямую зависит от способности эффективно транслировать квантовые схемы между различными аппаратными платформами. Каждая платформа обладает уникальной архитектурой и набором управляющих элементов, что требует адаптации алгоритмов для конкретного оборудования. Эта необходимость трансляции аналогична переводу с одного языка программирования на другой, но значительно сложнее из-за хрупкости квантовых состояний и ограничений существующих технологий. Успешное решение задачи трансляции позволит использовать преимущества каждой платформы и откроет путь к созданию мощных и универсальных квантовых вычислительных систем, способных решать задачи, недоступные классическим компьютерам.

Традиционные методы трансляции квантовых схем сталкиваются со значительными трудностями из-за сложности процесса, особенно при работе с физическими ограничениями существующих квантовых процессоров. Ограниченная связность между кубитами — когда не все кубиты могут напрямую взаимодействовать — требует введения дополнительных операций, таких как перестановка кубитов, что увеличивает длину схемы и вносит ошибки. Кроме того, неполнота набора управляющих вентилей на конкретном аппаратном обеспечении вынуждает разбивать логические операции на более простые, доступные вентили, что также усложняет схему и снижает её эффективность. Эти факторы в совокупности создают экспоненциальный рост вычислительной нагрузки при трансляции, что делает задачу оптимизации квантовых схем крайне сложной и требует разработки новых алгоритмов и подходов для преодоления этих ограничений и реализации потенциала квантовых вычислений.

Ограничения в трансляции квантовых схем создают серьезное препятствие для реализации всего потенциала квантовых устройств ближайшего будущего. Существующие методы оказываются неэффективными при работе со сложными схемами и ограниченными возможностями аппаратного обеспечения, что приводит к замедлению вычислений и увеличению количества ошибок. Данная проблема является ключевым фактором, сдерживающим прогресс в области квантовых технологий и требует разработки принципиально новых подходов к трансляции, способных эффективно адаптировать алгоритмы к конкретным архитектурам и минимизировать потери производительности. Поиск инновационных решений в этой области является необходимым условием для раскрытия всего спектра возможностей квантовых вычислений и их практического применения.

Трансформеры на службе квантовых алгоритмов

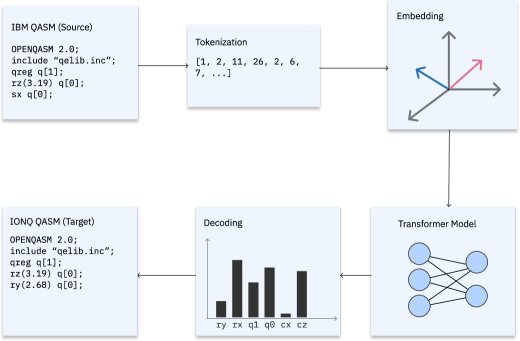
Предлагается использование архитектуры Transformer — проверенной модели последовательность-в-последовательность — для представления и манипулирования квантовыми схемами. Transformer, изначально разработанный для обработки естественного языка, позволяет эффективно моделировать зависимости между элементами последовательности, что делает его применимым к задачам обработки квантовых алгоритмов. В контексте квантовых вычислений, это позволяет представлять квантовые схемы как последовательности токенов, что открывает возможности для обучения модели сложным преобразованиям и оптимизациям, превосходящим возможности традиционных, основанных на правилах, методов. Архитектура Transformer, благодаря механизму внимания, позволяет модели эффективно обрабатывать длинные последовательности операций, что особенно важно для сложных квантовых схем.

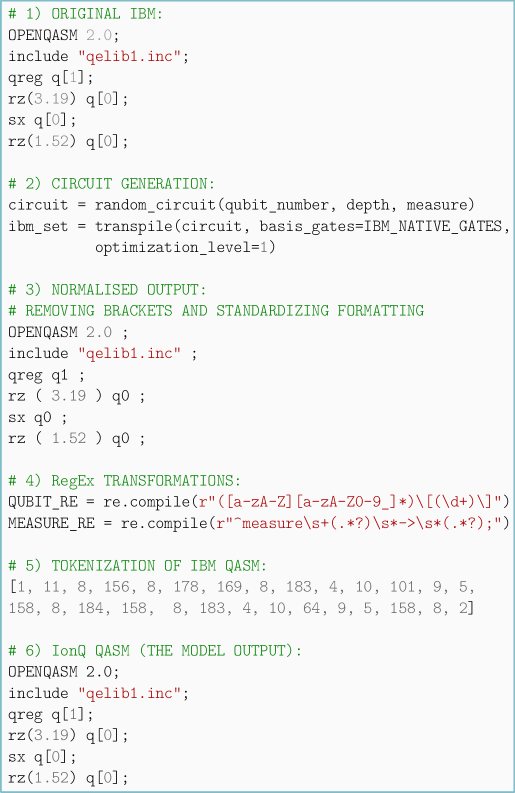
Квантовые схемы, представленные в языке QASM, подвергаются токенизации — процессу разбиения исходного текста на отдельные элементы (токены). Каждый токен, представляющий собой оператор, регистр или иной элемент схемы, преобразуется в уникальное числовое представление — целочисленный идентификатор. Этот процесс позволяет представить квантовую схему как последовательность чисел, пригодную для обработки архитектурой Transformer, которая изначально предназначена для работы с последовательностями данных. Например, оператор $Hadamard$ может быть представлен числом 1, $CNOT$ — числом 2, и так далее. Использование числовых представлений обеспечивает эффективную обработку данных и позволяет модели извлекать закономерности и зависимости между различными элементами квантовой схемы.

Использование архитектуры Transformer позволяет модели выявлять сложные взаимосвязи между различными последовательностями квантовых гейтов и их оптимальными эквивалентами. В отличие от методов, основанных на жестких правилах, Transformer способен обучаться на больших объемах данных, что позволяет ему находить более эффективные преобразования квантовых схем. Этот подход особенно полезен для задач оптимизации схем, где традиционные методы часто оказываются неэффективными из-за экспоненциального роста пространства поиска. Модель, обученная на данных о преобразованиях схем, может предсказывать оптимальные последовательности гейтов, минимизируя количество необходимых гейтов или время выполнения квантового алгоритма, что существенно повышает производительность и масштабируемость квантовых вычислений.

Кодирование структуры квантовых схем: позиционные подсказки

Для передачи информации о последовательности операций в квантовой схеме используется позиционное кодирование. Этот метод заключается во встраивании информации о позиции каждого токена в последовательность, что позволяет модели различать различные структуры схем. Позиционное кодирование добавляет к каждому токену вектор, отражающий его позицию, позволяя Transformer учитывать порядок следования операций при обработке данных. В результате, модель способна корректно интерпретировать квантовые схемы, учитывая не только типы используемых гейтов, но и их последовательность выполнения.

Для обеспечения различения различных структур квантовых схем, применяется техника позиционного кодирования, которая внедряет информацию о позиции каждого токена в последовательности. В процессе кодирования, каждому токену, представляющему элемент схемы (например, квантовый регистр или гейт), присваивается уникальный вектор, отражающий его местоположение в общей последовательности операций. Этот вектор добавляется к векторному представлению токена, позволяя модели учитывать порядок следования элементов схемы при обработке и, следовательно, корректно интерпретировать её структуру. Таким образом, позиционное кодирование предоставляет модели информацию о синтаксисе квантовой схемы, необходимую для точного перевода или анализа.

Механизм самовнимания (self-attention) в архитектуре Transformer позволяет модели оценивать значимость различных операций (гейтов) в квантовой схеме. В процессе обработки последовательности токенов, представляющих квантовую схему, самовнимание вычисляет веса, определяющие вклад каждого гейта в конечное представление схемы. Эти веса формируются на основе взаимосвязей между гейтами, позволяя модели идентифицировать критически важные зависимости и игнорировать несущественные. В результате, Transformer способен эффективно взвешивать вклад каждого гейта, что необходимо для оптимальной трансляции и обработки квантовых схем, особенно в случаях, когда порядок операций существенно влияет на результат.

Оптимизация перевода: комбинированная функция потерь

Модель Transformer обучается с использованием комбинированной функции потерь, включающей в себя как перекрестную энтропию, так и потерю соответствия. Перекрестная энтропия ($H(p,q)$) минимизирует расхождение между предсказанным распределением вероятностей токенов и фактическим распределением в целевом тексте, обеспечивая синтаксическую корректность перевода. Параллельно, функция потерь соответствия оценивает степень сходства между исходной и переведенной квантовыми схемами, напрямую измеряя функциональную эквивалентность. Комбинирование этих двух компонент позволяет одновременно оптимизировать точность предсказания последовательности токенов и семантическую близость переведенной схемы к исходной.

В процессе обучения модели-трансформатора используется комбинированная функция потерь, состоящая из перекрестной энтропии и потерь на соответствие (fidelity loss). Перекрестная энтропия ($H(p,q)$) обеспечивает точное предсказание последовательности токенов в переведенной схеме, минимизируя разницу между предсказанным распределением вероятностей и истинным распределением. Потери на соответствие напрямую измеряют сходство между исходной и переведенной квантовыми схемами, используя метрики, такие как среднее расстояние Хэмминга или сходство состояний, для оценки сохранения функциональной эквивалентности. Комбинация этих двух типов потерь позволяет модели одновременно достигать синтаксической корректности и функционального соответствия при переводе квантовых схем.

Комбинированный подход к обучению, использующий одновременно функцию потерь кросс-энтропии и функцию потерь, оценивающую соответствие квантовых схем, обеспечивает достижение как синтаксической корректности, так и функциональной эквивалентности при трансляции. Кросс-энтропия оптимизирует точность предсказания последовательности токенов, в то время как функция потерь, оценивающая соответствие схем, напрямую измеряет сходство между исходной и транслированной схемами. Это позволяет модели не только генерировать грамматически правильные последовательности операций, но и гарантировать, что транслированная схема выполняет ту же функцию, что и исходная, обеспечивая высокое качество трансляции квантовых схем и минимизируя отклонения в результатах вычислений.

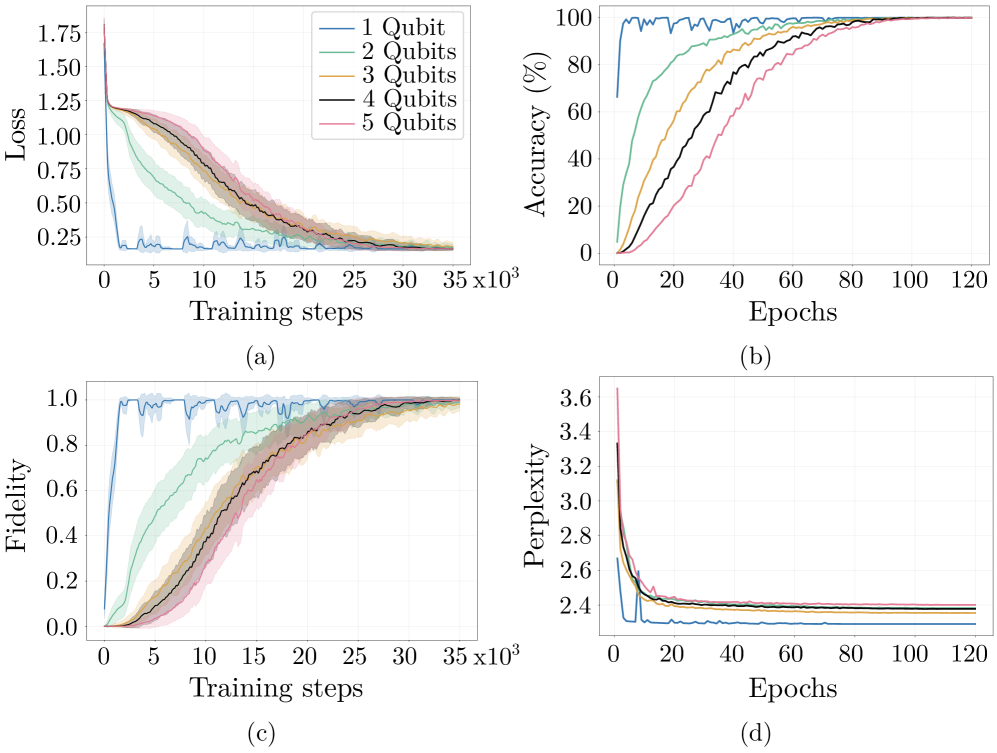
К масштабируемому и надежному переводу квантовых схем

Исследование демонстрирует перспективный подход к масштабируемому и надежному преобразованию квантовых схем посредством использования архитектур Transformer. Данная методика позволяет эффективно сопоставлять квантовые алгоритмы, разработанные для различных аппаратных платформ, преодолевая ограничения традиционных методов трансляции. В основе лежит способность Transformer-моделей к параллельной обработке и улавливанию сложных зависимостей в данных, что критически важно для оптимизации квантовых схем. Благодаря этому, достигается не только высокая точность преобразования, но и потенциальная возможность масштабирования системы для работы со все более сложными квантовыми вычислениями, открывая путь к более эффективному использованию разнообразного квантового оборудования и расширению возможностей квантовых технологий.

Разработанный транспайлер на основе архитектуры Transformer достиг точности более 99,98% при переводе квантовых схем между наборами гейтов IBM и IonQ, что демонстрирует высокую эффективность и точность межплатформенной трансляции квантовых схем. Данный результат свидетельствует о возможности точного переноса квантовых алгоритмов между различными типами квантового оборудования, преодолевая ограничения, связанные с различиями в наборах доступных операций. Такая точность позволяет существенно снизить вероятность ошибок при выполнении вычислений на различных квантовых платформах, открывая перспективы для более широкого использования разнообразных квантовых ресурсов и оптимизации производительности квантовых алгоритмов.

Сложность разработанной модели для трансляции квантовых схем закономерно увеличивается с ростом числа кубитов, длины схемы и требуемой точности. Исследования показали, что вычислительная сложность масштабируется как $O(nf(n)log_c(n*f(n)/ε))$,где$n$-числокубитов,$f(n)$-функция,описывающаясложностьквантовойсхемы,а$ε$ — требуемая точность. Данная зависимость позволяет прогнозировать вычислительные ресурсы, необходимые для трансляции схем различной сложности, и оптимизировать процесс для конкретного аппаратного обеспечения. Такое масштабирование обеспечивает практическую применимость модели для работы с более крупными и сложными квантовыми вычислениями, сохраняя при этом контролируемую вычислительную нагрузку.

Данный подход позволяет преодолеть ограничения, свойственные традиционным методам трансляции квантовых схем. В отличие от существующих решений, требующих значительных вычислительных ресурсов и часто неспособных эффективно адаптироваться к различным архитектурам квантового оборудования, представленная система обеспечивает эффективное использование разнообразных квантовых платформ. Это достигается за счет использования архитектуры Transformer, которая позволяет модели обучаться на больших объемах данных и обобщать полученные знания для работы с различными наборами гейтов и топологиями кубитов. В результате, становится возможным автоматическое преобразование квантовых алгоритмов, разработанных для одной аппаратной платформы, в эквивалентные схемы, оптимизированные для другой, что значительно расширяет возможности реализации квантовых вычислений и способствует более широкому внедрению квантовых технологий.

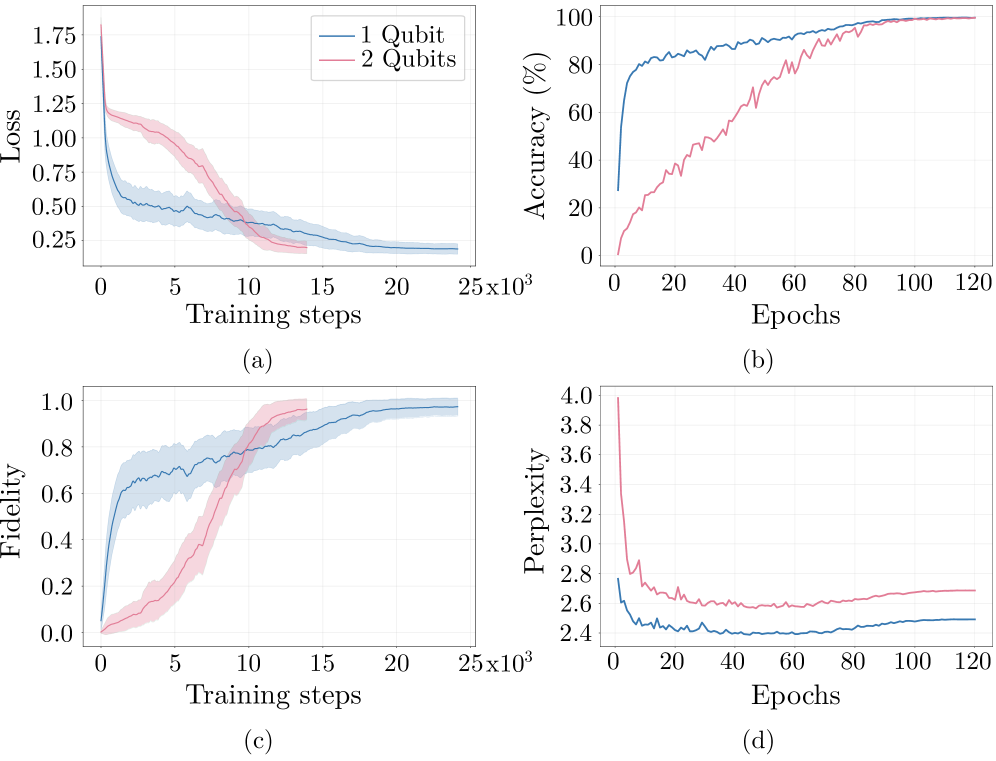
Исследование показывает, что трансформеры способны к трансляции квантовых схем между различными аппаратными платформами с поразительной точностью. Это напоминает вечную борьбу между теорией и практикой. Разработчики строят элегантные модели, а продакшен, как всегда, находит способ их сломать или, в данном случае, успешно адаптировать к реальному железу. Как сказал Эрвин Шрёдингер: «Всё новое — это старое, только с другим именем и теми же багами». Транспиляция квантовых схем, основанная на трансформерах, лишь подтверждает эту истину — оптимизация, хоть и реализованная через сложные алгоритмы, по сути, сводится к переупаковке уже известных решений для достижения приемлемой производительности на конкретном оборудовании. И пусть точность превышает 99.98%, всегда найдется баг, который вылезет в самый неподходящий момент.

Что дальше?

Демонстрация возможности трансляции квантовых схем посредством трансформеров, безусловно, добавляет ещё один инструмент в арсенал компиляторов. Однако, стоит помнить: каждая «оптимизация» — это лишь отсрочка неизбежного столкновения с реальным железом. Достижение 99.98% точности — это впечатляюще, но вопрос в том, что произойдет с оставшимися 0.02% в масштабе сотен тысяч гейтов. Иначе говоря, сейчас задача — не столько научиться идеально транслировать, сколько выработать устойчивость к ошибкам, которые всё равно возникнут.

Теорема Соловая-Китайева, лежащая в основе компиляции, подразумевает экспоненциальный рост сложности. Трансформеры эту сложность не отменяют, они лишь перекладывают её на этап обучения модели. Вполне вероятно, что в будущем возникнет необходимость в разработке «мета-трансформаторов», способных адаптироваться к новым архитектурам без переобучения. Архитектура — это не схема, а компромисс, переживший деплой.

В конечном счете, все эти изящные алгоритмы — лишь способ временно обмануть законы физики. Всё, что оптимизировано, рано или поздно оптимизируют обратно. Задача не в том, чтобы создать идеальный компилятор, а в том, чтобы построить систему, способную к самовосстановлению после неизбежных сбоев. Мы не рефакторим код — мы реанимируем надежду.

---

Оригинал статьи: https://arxiv.org/pdf/2512.09834.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/