Квантовые технологии
Квантовые симуляции: Фермионы на службе у кубитов
Автор: Денис Аветисян
Новый подход позволяет эффективно моделировать фермионные системы, используя возможности квантовых симуляторов на основе кубитов.

В статье представлен метод отображения фермионных степеней свободы на кубиты с использованием формализма второй квантизации, позволяющий исследовать корреляционные функции и запутанность.
Моделирование фермионных многочастичных систем на кубитных квантовых компьютерах сталкивается с существенными трудностями из-за накладных расходов, связанных с кодированием фермионной статистики. В данной работе, ‘Qubits in second quantisation in fermionic simulators’, предлагается сопоставить фермионные моды с «кубитами во втором квантовании», что позволяет представить фермионные гейты как вращения этих кубитов и адаптировать методы, разработанные для кубитных систем. Посредством данной схемы сопоставления, измерение двух- и четырехточечных корреляторов в фермионных симуляторах преобразуется в задачу на графах, позволяя оптимизировать настройки измерений аналитическими и алгоритмическими методами. Возможно ли дальнейшее развитие этого подхода для эффективного моделирования более сложных фермионных систем и расширения возможностей квантовых симуляторов?
За пределами кубитов: моделирование фермионных систем
Моделирование сложных фермионных систем играет ключевую роль в современной науке о материалах и фундаментальной физике, позволяя исследовать свойства веществ и предсказывать их поведение на микроскопическом уровне. Однако, применение традиционных квантовых компьютеров к таким задачам сталкивается со значительными трудностями. Проблема заключается в том, что для адекватного представления фермионов на кубитах требуется экспоненциально растущее количество последних, что делает моделирование больших и сложных систем практически невозможным. Это связано с тем, что фермионы подчиняются принципу Паули, запрещающему двум идентичным фермионам занимать одно и то же квантовое состояние, что требует особого подхода к их кодированию и моделированию. Преодоление этих вычислительных барьеров является важнейшей задачей для развития квантовых технологий и открытия новых материалов с уникальными свойствами.
Прямое отображение фермионных систем на кубиты часто требует экспоненциального увеличения вычислительных ресурсов, что становится серьезным препятствием для масштабируемости квантовых вычислений. В частности, для точного моделирования взаимодействующих фермионов, таких как электроны в материалах, необходимо описывать все возможные квантовые состояния, количество которых растет экспоненциально с числом фермионов. Это означает, что для моделирования даже относительно небольших систем может потребоваться огромное количество кубитов, превосходящее возможности современных и даже будущих квантовых компьютеров. Следовательно, поиск альтернативных подходов, позволяющих эффективно представлять фермионные системы с использованием ограниченного числа кубитов, является критически важной задачей для развития квантовой симуляции материалов и фундаментальной физики. Такие подходы должны стремиться к компактному кодированию информации о фермионных состояниях, избегая экспоненциального нарастания сложности.
Разработка симулятора, основанного на фермионных строительных блоках, представляет собой перспективный подход к моделированию сложных фермионных систем, которые имеют решающее значение для материаловедения и фундаментальной физики. В отличие от прямого отображения фермионов на кубиты, требующего экспоненциального увеличения ресурсов, данный метод позволяет использовать преимущества кубитных технологий, таких как перекрывающаяся томография. Это, в свою очередь, открывает возможности для эффективного анализа и исследования коррелированных фермионных систем, преодолевая ограничения, связанные с масштабируемостью традиционных квантовых вычислений. Подобный подход позволяет напрямую исследовать фермионные свойства, что особенно важно для понимания высокотемпературной сверхпроводимости и других сложных явлений в конденсированных средах, и значительно расширяет возможности квантового моделирования.
Фермионная платформа-симулятор: архитектура и принципы
Наша фермионная платформа-симулятор использует массивы оптических пинцетов для точного захвата и манипулирования отдельными фермионными атомами. В данной конфигурации, атомы удерживаются в отдельных потенциальных ямах, создаваемых сфокусированными лазерными лучами. Массив пинцетов позволяет достичь высокой степени контроля над положением каждого атома, обеспечивая возможность индивидуального обращения и взаимодействия между ними. Используемая технология позволяет удерживать атомы в течение продолжительного времени, необходимого для выполнения сложных квантовых операций и моделирования фермионных систем. Точность позиционирования и стабильность удержания являются ключевыми параметрами, определяющими производительность и достоверность результатов моделирования.
Платформа фермионного симулятора использует нативные логические вентили — вентиль туннелирования и вентиль взаимодействия — для управления взаимодействиями между захваченными атомами. Вентиль туннелирования реализует перенос состояния между соседними атомами, используя контролируемое туннелирование волновых функций. Вентиль взаимодействия, в свою очередь, позволяет модулировать силу взаимодействия между определенными парами атомов, изменяя параметры оптических потенциалов. Комбинация этих двух нативных вентилей обеспечивает универсальный набор операций для реализации произвольных фермионных гамильтонианов без необходимости в дополнительных операциях декомпозиции или аппроксимации, что повышает эффективность и точность симуляции.
Платформа фермионного симулятора обеспечивает прямой и эффективный способ реализации сложных фермионных гамильтонианов, избегая накладных расходов, связанных с отображением на кубиты. В отличие от подходов, требующих кодирования фермионных операторов в кубитные представления, наша платформа позволяет напрямую манипулировать фермионными степенями свободы. Это значительно упрощает моделирование и снижает вычислительную сложность. Кроме того, платформа поддерживает использование методов перекрывающейся томографии (overlapping tomography) для всесторонней характеризации состояния системы и проверки точности реализованных гамильтонианов, что позволяет оценивать когерентность и точность управления фермионными атомами.
Характеризация фермионных корреляций: наблюдаемые и методы
Для валидации симулятора используются ключевые наблюдаемые величины, такие как Двухточечный коррелятор и Четырехточечный коррелятор. Эти корреляторы количественно оценивают корреляции между фермионными атомами, предоставляя информацию о многочастичной физике моделируемой системы. Двухточечный коррелятор, обозначаемый как G^{(2)}(x, x’), характеризует вероятность одновременного обнаружения фермиона в точках и x’. Четырехточечный коррелятор, , предоставляет информацию о более сложных корреляциях и используется для выявления и анализа взаимодействий между частицами. Измерение этих корреляторов позволяет проверить корректность реализации взаимодействий в симулируемой системе и подтвердить ее адекватность для изучения физических явлений.
Двух- и четырехточечные корреляторы являются ключевыми наблюдаемыми для анализа многочастичной физики в смоделированной системе фермионных атомов. Измерение этих корреляторов позволяет проверить корректность реализации взаимодействий между частицами и оценить степень квантовой корреляции в системе. Анализ формы и величины корреляторов предоставляет информацию о структуре волновой функции многих тел и позволяет выявить наличие или отсутствие определенных типов квантовых состояний, таких как пары Купера или коллективные возбуждения. Сравнение измеренных корреляторов с теоретическими предсказаниями, полученными из моделей многих тел, служит для валидации симулятора и подтверждения его способности воспроизводить сложные квантовые явления.
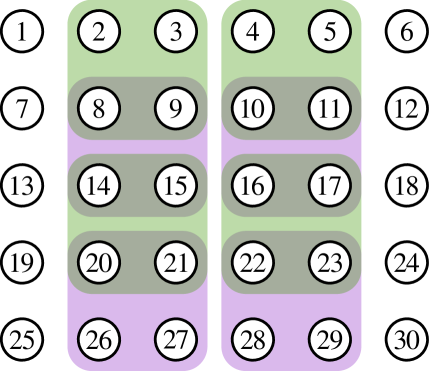
Для повышения эффективности измерений и снижения ошибок при характеризации корреляций фермионов используется метод перекрывающейся томографии, поддерживаемый покрытием рёбер кликами. Этот подход позволяет оптимизировать параметры измерений, требуя всего установок для полного графа с узлами. В частности, для 4-модовой системы достигается 20 различных установок измерений, а для 6-модовой системы — 70 установок, что существенно снижает временные и вычислительные затраты по сравнению с традиционными методами томографии.
Исследование многочастичной физики на решетках: новые горизонты
Фермионный симулятор предоставляет возможность детального изучения поведения фермионных атомов, организованных в различные кристаллические решетки, включая прямоугольные, треугольные и гексагональные структуры. Исследование этих геометрических конфигураций имеет ключевое значение для моделирования конденсированных сред и понимания возникающих в них явлений, таких как сверхпроводимость или магнетизм. Используя симулятор, ученые могут контролировать взаимодействие между атомами и параметры решетки, что позволяет исследовать фазовые переходы и образование экзотических квантовых состояний материи, выходящих за рамки классического понимания. Этот подход открывает новые перспективы для разработки материалов с уникальными свойствами и создания квантовых технологий будущего.
Изучение различных геометрических структур решеток, таких как прямоугольные, треугольные и гексагональные, играет фундаментальную роль в моделировании конденсированных сред и исследовании возникающих явлений. Эти структуры служат основой для приближения сложных взаимодействий между частицами в реальных материалах, позволяя ученым прогнозировать и понимать их квантовое поведение. В частности, изучение фермионных атомов, расположенных в этих решетках, помогает раскрыть механизмы фазовых переходов и формирование экзотических квантовых состояний, от сверхпроводимости до топологических изоляторов. Понимание этих явлений, возникающих из коллективного поведения частиц в структурированных системах, имеет решающее значение для разработки новых материалов с уникальными свойствами и применения в передовых технологиях.
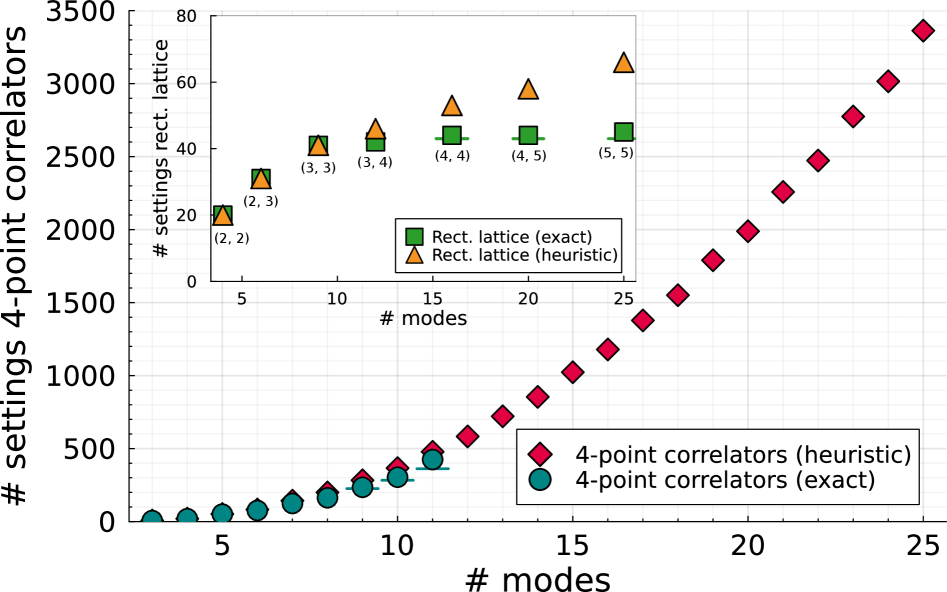
Исследование поведения фермионных атомов в различных решетчатых структурах позволяет изучать фазовые переходы и формирование экзотических квантовых состояний. Настройка взаимодействия между частицами и параметров решетки открывает возможность моделирования сложных систем конденсированного состояния вещества. Особенностью разработанного метода является его масштабируемость: для характеристики прямоугольных решеток требуется постоянное количество — 80 параметров, вне зависимости от размера исследуемой системы. Это значительно упрощает анализ и позволяет эффективно изучать поведение фермионов в широком диапазоне условий, приближая нас к пониманию фундаментальных свойств материи и потенциальным технологическим применениям квантовых явлений.
Исследование демонстрирует, что попытки построить стабильные системы для моделирования фермионных систем обречены на провал, если исходить из классического представления о детерминированности. Вместо этого, предлагаемый подход, основанный на представлении фермионных мод как кубитов во второй квантизации, признает неотъемлемую вероятностную природу квантовых процессов. Как заметил Луи де Бройль: «Каждому определенному явлению соответствует ряд вероятностей». Этот принцип отражается в методе, где корреляционные функции извлекаются через перекрывающуюся томографию, а не через прямое измерение. Стабильность здесь — это иллюзия, хорошо кэшированная в математической модели, а хаос — это язык природы, говорящий о бесконечном множестве возможных состояний.
Куда Ведет Этот Сад?
Представленная работа, подобно тщательному привью молодого побега, демонстрирует возможность отображения фермионных систем на кубитные платформы. Однако, не стоит обольщаться иллюзией полного контроля. Отображение — это всегда упрощение, всегда потеря информации. Чем сложнее фермионная система, тем более изощренным становится этот компромисс, и тем быстрее растет техдолг, скрытый в деталях отображения.
Задача, заключающаяся в эффективном измерении корреляционных функций в таких системах, не решена, а лишь переформулирована. Переход к кубитным измерениям открывает новые возможности, но и новые сложности. Устойчивость системы не в изоляции отдельных кубитов, а в их способности прощать ошибки друг друга, в способности адаптироваться к несовершенству физической реализации. Следующим шагом видится не столько в совершенствовании алгоритмов отображения, сколько в разработке методов, позволяющих извлекать полезную информацию из зашумленных данных, в создании садов, способных выживать в неблагоприятных условиях.
Истинный прогресс, вероятно, кроется не в создании более мощных машин для моделирования, а в понимании, что система — это не конструкция, а экосистема. Попытка построить идеальную модель обречена на неудачу; необходимо научиться выращивать систему, способную адаптироваться и эволюционировать, подобно живому организму. И тогда, возможно, удастся увидеть не только то, что мы хотели измерить, но и то, что ускользало от нас до сих пор.
Оригинал статьи: https://arxiv.org/pdf/2512.11726.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Статья также опубликована на личном сайте автора.