Квантовые вычисления для молекул: оптимизация ресурсов

---

Новое исследование демонстрирует, как эффективно оценить и снизить вычислительные затраты при моделировании молекул с помощью квантового алгоритма VQE.

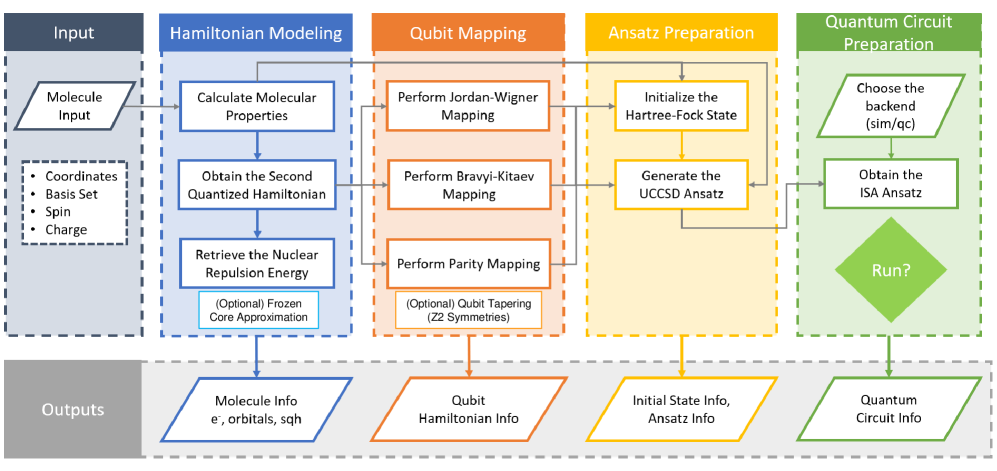
Оценка влияния различных методов отображения фермионов в кубиты и упрощения гамильтонианов на ресурсы, необходимые для вариационного квантового решателя.

Несмотря на значительный прогресс в квантовых вычислениях, точное моделирование молекул остается сложной задачей, требующей всё большего количества кубитов. В работе, посвященной ‘Resource Estimation for VQE on Small Molecules: Impact of Fermion Mappings and Hamiltonian Reductions’, систематически анализируются требования к вычислительным ресурсам для алгоритма Variational Quantum Eigensolver (VQE) при различных схемах кодирования фермионов и стратегиях упрощения гамильтониана. Показано, что оптимизация преобразований фермионов в кубиты в сочетании с симметричными сокращениями позволяет снизить количество необходимых кубитов до 50% и количество квантовых гейтов до 45 раз для исследуемых молекулярных систем. Какие дальнейшие оптимизации позволят эффективно использовать возможности квантового оборудования для решения задач современной химии и материаловедения?

---

Молекулярная Электронная Структура: Вычислительные Пределы

Точное моделирование электронной структуры молекул имеет первостепенное значение для открытия новых материалов и углубленного понимания химических процессов. Однако, классические вычислительные методы сталкиваются с проблемой экспоненциального роста требуемых ресурсов по мере увеличения размера исследуемой системы. Это означает, что сложность вычислений возрастает не линейно, а экспоненциально с добавлением каждого нового атома или электрона, что быстро делает моделирование сложных молекул и материалов практически невозможным даже на самых мощных современных компьютерах. Например, для точного описания взаимодействий $N$ электронов требуется вычислительная мощность, растущая как $2^N$, что делает решение задачи для реалистичных систем чрезвычайно трудоемким. Поэтому поиск эффективных методов преодоления этого экспоненциального масштабирования является ключевой задачей современной теоретической химии и физики конденсированного состояния.

Традиционные методы расчета электронной структуры молекул, такие как метод Хартри-Фока и его более продвинутые варианты, предъявляют чрезвычайно высокие требования к вычислительным ресурсам. Сложность этих методов растет экспоненциально с увеличением числа атомов в моделируемой системе, что существенно ограничивает возможность проведения симуляций сложных материалов и молекул. Даже использование мощнейших суперкомпьютеров часто не позволяет адекватно описать системы, содержащие более нескольких десятков атомов, что создает серьезное препятствие для моделирования реальных материалов и разработки новых химических соединений. Необходимость в более эффективных вычислительных подходах становится особенно острой в областях материаловедения, катализа и разработки лекарств, где понимание электронной структуры является ключевым для предсказания свойств и реакционной способности веществ.

Основная сложность моделирования электронного строения молекул заключается в эффективном представлении многочастичной квантовомеханической задачи, обусловленной взаимодействием электронов. Взаимодействие между электронами не является независимым; каждый электрон испытывает влияние от всех остальных, что приводит к экспоненциальному росту сложности с увеличением числа электронов в системе. Для точного описания необходимо учитывать корреляции между электронами, которые выходят за рамки приближений, используемых в более простых методах, таких как метод Хартри-Фока. Это означает, что для моделирования даже умеренно сложных молекул требуются огромные вычислительные ресурсы и продвинутые алгоритмы, способные эффективно учитывать $N$-электронные корреляции, где $N$ — число электронов в системе. Поиск эффективных методов для решения этой многочастичной задачи остается ключевой проблемой в современной вычислительной химии и физике материалов.

Вариационный Квантовый Решатель: Гибридный Подход

Вариационный квантовый решатель уравнений ($VQE$) представляет собой гибридный квантово-классический алгоритм, предназначенный для нахождения основного состояния энергии молекул. В его основе лежит использование квантового компьютера для подготовки и измерения пробных волновых функций, описывающих квантовое состояние молекулы. Результаты этих измерений передаются классическому компьютеру, который оптимизирует параметры квантовой схемы с целью минимизации энергии. Такой подход позволяет использовать преимущества обоих типов вычислений, обходя ограничения, присущие исключительно квантовым или классическим алгоритмам, и делает $VQE$ перспективным инструментом для квантовой химии и материаловедения.

Вариационный квантовый решатель (VQE) использует квантовый компьютер для подготовки и измерения пробных волновых функций, представляющих собой приближенные решения уравнения Шредингера. Квантовая схема, реализующая эту подготовку, оперирует кубитами и их суперпозициями для генерации различных состояний. Полученные результаты измерений, представляющие собой вероятности нахождения системы в определенных состояниях, передаются классическому компьютеру. Классический компьютер использует алгоритмы оптимизации для итеративного изменения параметров квантовой схемы, стремясь минимизировать энергию системы, рассчитанную на основе результатов квантовых измерений. Этот гибридный подход позволяет использовать сильные стороны как квантовых, так и классических вычислений для приближенного нахождения основного состояния молекулы.

Эффективность алгоритма VQE (Variational Quantum Eigensolver) напрямую зависит от выбора квантовой схемы, используемой для представления волновой функции. В частности, схема UCCSD (Unitary Coupled Cluster Singles and Doubles) является одним из наиболее часто используемых подходов, поскольку она обеспечивает хорошее приближение к истинной волновой функции для многих молекул. Однако, сложность схемы UCCSD растет экспоненциально с количеством кубитов, что ограничивает ее применимость к большим системам. Выбор подходящего анзаца, такого как UCCSD, требует компромисса между точностью представления волновой функции и вычислительной сложностью реализации на квантовом компьютере. Альтернативные анзацы, такие как Hardware Efficient Ansatz, могут быть более подходящими для конкретных квантовых архитектур, но могут потребовать большего количества параметров для достижения той же точности.

Стратегии Отображения Фермионных Операторов: Сокращение Требований к Кубитам

Отображение фермионных операторов на кубитные является необходимым этапом для реализации вариационного квантового эвристического алгоритма (VQE) на квантовом компьютере. Однако, этот процесс часто приводит к значительному увеличению числа необходимых кубитов. Это связано с тем, что фермионы описывают частицы с антисимметричными волновыми функциями, требующими использования нескольких кубитов для представления каждого фермионного состояния. В частности, для представления одного фермиона обычно требуется два кубита, что приводит к линейному увеличению потребления кубитов с ростом числа фермионов в квантово-химической модели. Таким образом, эффективное отображение фермионных операторов является критически важной задачей для реализации VQE на современных квантовых компьютерах с ограниченным числом кубитов.

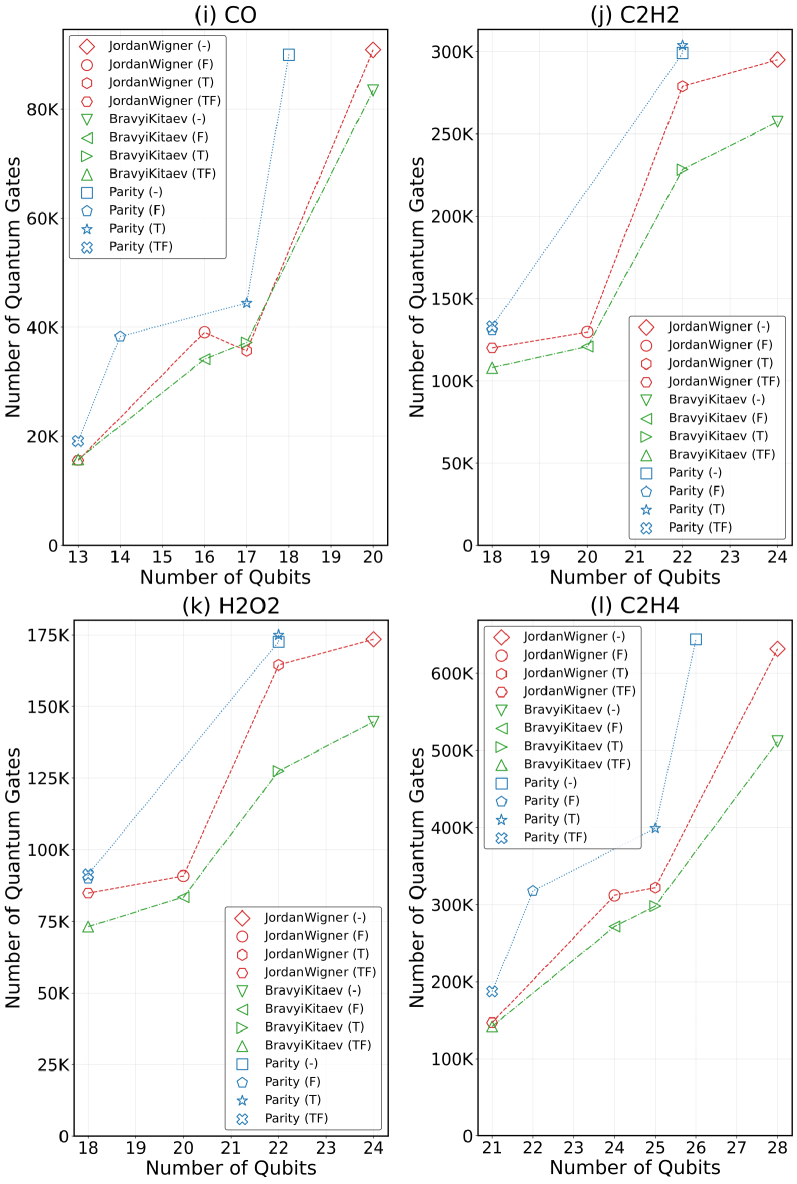
Преобразования Жордана-Вигнера (JW) и Бравии-Китайева (BK) являются широко используемыми методами отображения фермионных операторов в кубитные. В то время как JW-преобразование просто и интуитивно понятно, оно часто приводит к экспоненциальному увеличению числа необходимых кубитов. BK-преобразование, напротив, обеспечивает более компактное представление, уменьшая количество требуемых кубитов за счет использования альтернативной структуры соответствия между фермионами и кубитами. В результате, для реализации вариационного квантового эмулятора (VQE) для задач квантовой химии, BK-преобразование обычно предпочтительнее, поскольку позволяет снизить вычислительные затраты и требования к аппаратным ресурсам.

Альтернативные методы, такие как отображение чётности (Parity Mapping) и отсечение по симметрии (Symmetry Tapering), позволяют дополнительно снизить требования к количеству кубитов за счет использования присущих молекулярным системам симметрий. Отображение чётности эффективно кодирует информацию о фермионном заполнении, уменьшая потребность в кубитах для представления фермионных операторов. Отсечение по симметрии исключает из рассмотрения непригодные состояния, основываясь на симметриях молекулы. Комбинированное применение этих методов, с последующей оптимизацией квантовой схемы, позволяет достичь сокращения количества необходимых кубитов до 50% в ряде молекулярных систем, что существенно снижает требования к ресурсам квантового компьютера для выполнения вариационных расчетов.

Оценка Ресурсов и Сложность Схем: Реалистичные Ограничения

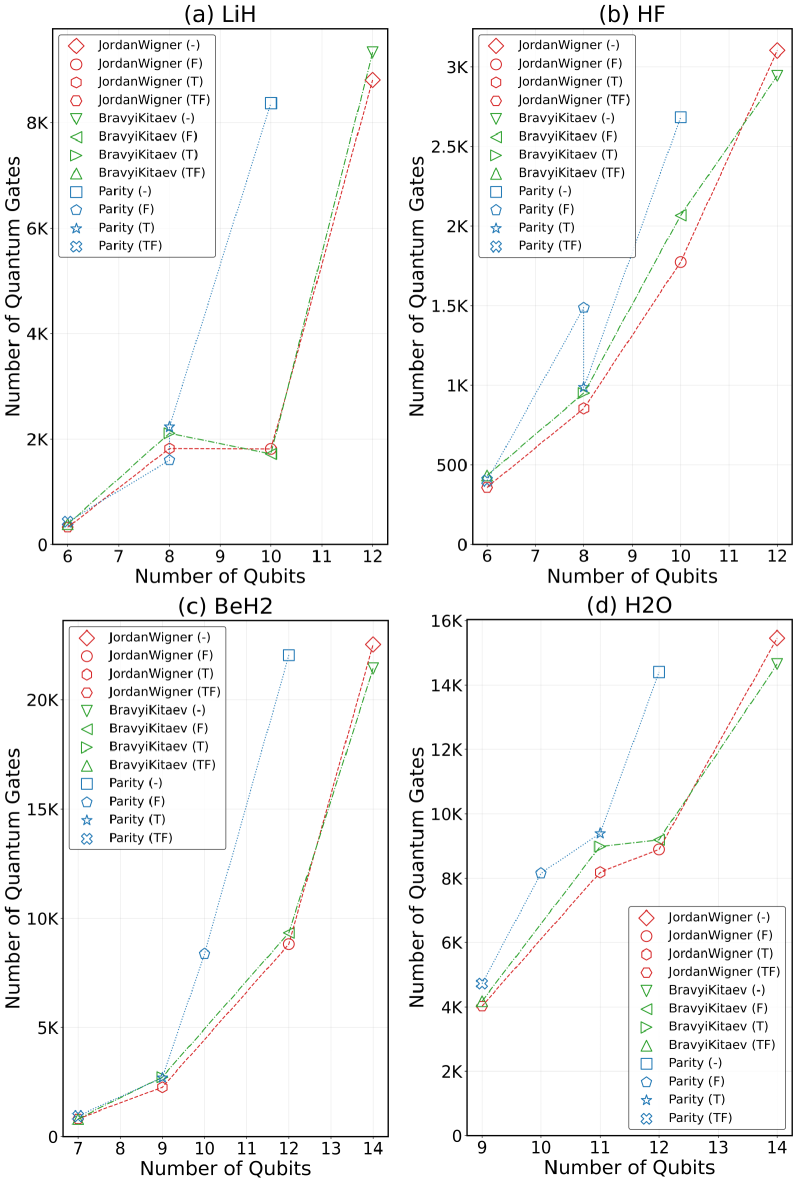
Точная оценка ресурсов — количественное определение количества кубитов, числа логических вентилей и глубины схемы — имеет решающее значение для оценки реализуемости симуляций вариационного квантового эвристического алгоритма (VQE). Без тщательного анализа этих параметров, невозможно достоверно предсказать, сможет ли конкретная квантовая схема эффективно работать на доступном оборудовании. Определение необходимых ресурсов позволяет исследователям выбирать наиболее подходящие алгоритмы и методы для решения конкретных задач, а также оценивать потенциальную пользу от использования квантовых вычислений по сравнению с классическими подходами. Кроме того, точная оценка ресурсов необходима для разработки стратегий оптимизации схемы и снижения требований к оборудованию, что особенно важно в контексте текущих ограничений квантовых технологий и доступности оборудования.

Приближение замороженного ядра является эффективным методом снижения вычислительных затрат в квантово-химических расчетах. Суть его заключается в исключении корреляции электронов внутренней оболочки из активного пространства, что значительно уменьшает размер волновой функции и, следовательно, количество необходимых кубитов и квантовых операций. В то время как электроны валентной оболочки определяют химические свойства молекулы, электроны внутренней оболочки, как правило, слабо взаимодействуют с внешней средой и вносят незначительный вклад в энергию. Исключение этих электронов из активного пространства позволяет существенно упростить расчеты без значительной потери точности, делая моделирование более сложных молекул доступным на существующих квантовых компьютерах и сокращая требования к ресурсам.

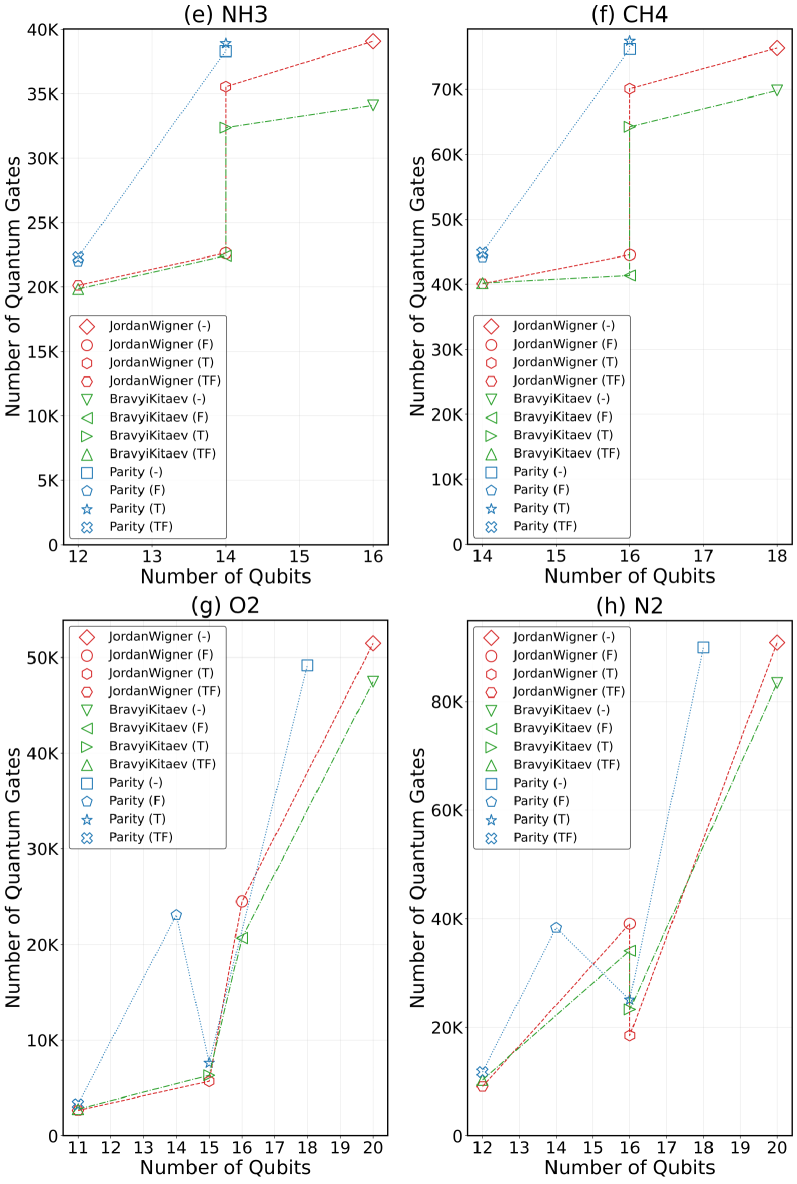
Для эффективной работы квантовых алгоритмов на современных, подверженных шумам квантовых устройствах (NISQ), крайне важно минимизировать глубину и количество квантовых гейтов в схеме. Исследование, посвященное оптимизации квантовых вычислений, продемонстрировало значительное снижение потребности в ресурсах — до 45 раз — за счет комбинированного применения различных техник оптимизации. Сокращение количества гейтов не только уменьшает вероятность накопления ошибок, возникающих из-за несовершенства оборудования, но и позволяет проводить более сложные вычисления в рамках ограничений доступных квантовых ресурсов. Это достижение открывает новые возможности для реализации квантовых алгоритмов на NISQ-устройствах и приближает перспективу практического применения квантовых вычислений.

Исследование демонстрирует, что оценка вычислительных ресурсов для квантовых алгоритмов, таких как VQE, требует строгой методологии. Авторы предлагают комплексный подход, включающий оптимизацию отображения фермионов в кубиты и сокращение гамильтониана, что позволяет значительно уменьшить количество необходимых кубитов и сложность квантовых схем. Этот подход критически важен для реализации молекулярных симуляций на существующих квантовых компьютерах. Как однажды заметил Джон Белл: «Играть в науку — значит играть с вероятностями, а не с абсолютной уверенностью». Данное исследование подтверждает эту мысль, показывая, что даже точные вычисления требуют тщательного анализа погрешностей и оптимизации ресурсов, чтобы получить достоверные результаты.

Что дальше?

Представленная работа, безусловно, демонстрирует возможность некоторой оптимизации в весьма болезненной области квантовых вычислений — а именно, в попытках заставить эти самые вычисления хоть что-то полезное делать. Уменьшение числа кубитов и сложности операций — это, конечно, хорошо. Однако, не стоит обманываться иллюзией прогресса. Данные не говорят сами за себя — их заставляют говорить, и в данном случае, “заставляют” посредством конкретного выбора фермионного отображения и сокращения гамильтониана. Другие варианты, возможно, окажутся более эффективными для других молекул, а универсального решения, судя по всему, не предвидится.

Следующим шагом, очевидно, является расширение тестового набора молекул. Но, что важнее, необходимо критически оценить применимость предложенного подхода к системам, выходящим за рамки «малых молекул». Чем больше визуализация “сокращений”, тем меньше проверка фундаментальных ограничений. Вопрос не в том, чтобы уместить задачу в существующее аппаратное обеспечение, а в том, чтобы понять, какие задачи вообще принципиально доступны квантовым алгоритмам, а какие — нет.

В конечном итоге, предложенная методология — это лишь один из инструментов в арсенале исследователя. Не стоит забывать, что сама концепция вариационного квантового решателя (VQE) основана на ряде приближений. Улучшение этих приближений, а не только оптимизация технических деталей, представляется более перспективной задачей. Иначе, мы рискуем потратить много усилий на оптимизацию алгоритма, который изначально не способен решить поставленную проблему.

---

Оригинал статьи: https://arxiv.org/pdf/2512.01605.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/