Квантовые вычисления: Новый взгляд на оценку ресурсов

---

Исследователи предложили метод точной оценки ресурсов, необходимых для квантовых алгоритмов, используя небольшие квантовые компьютеры для анализа ошибок симуляции.

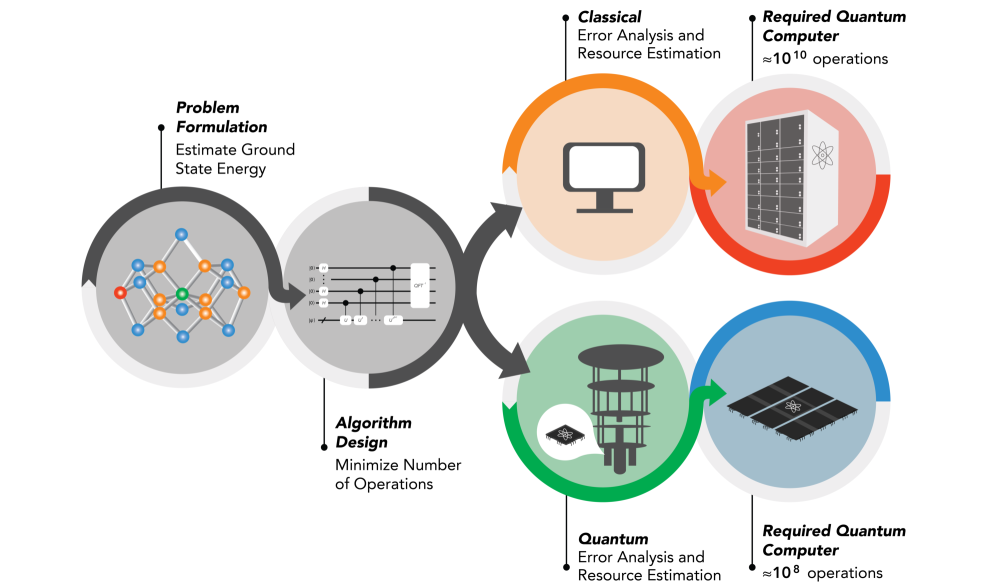
Предложенная методика позволяет более эффективно оценивать ресурсы для квантовых вычислений, приближая нас к демонстрации квантового превосходства в задачах оптимизации ресурсов.

Несмотря на значительный прогресс в разработке квантового оборудования, поиск практически значимых задач, демонстрирующих преимущество квантовых вычислений, остается сложной задачей. В работе ‘Quantum Advantage in Resource Estimation’ предлагается новый подход к решению этой проблемы, основанный на использовании квантовых компьютеров для точной оценки ресурсов, необходимых для выполнения более крупных квантовых алгоритмов, путем измерения ошибок симуляции. Показано, что разработанный квантовый алгоритм для оценки ошибок в методах Тротера может сократить время выполнения квантовых алгоритмов на три порядка величины для систем из ста кубитов, и эта тенденция усиливается с увеличением размера системы. Может ли этот метод стать первым практическим проявлением квантового преимущества, позволяя эффективно оценивать ресурсы для задач, недоступных для классических компьютеров?

---

Вычислительные Вызовы Квантового Моделирования

Моделирование квантовых систем играет ключевую роль в прогрессе химии и материаловедения, однако представляет собой серьезную вычислительную задачу. Сложность заключается в экспоненциальном росте требуемых ресурсов с увеличением числа взаимодействующих частиц. Даже для относительно небольших молекул или материалов, точное описание их квантового поведения требует огромных объемов памяти и процессорного времени, превосходящего возможности современных суперкомпьютеров. Это ограничивает возможность детального изучения сложных химических реакций, свойств новых материалов и разработки инновационных технологий, основанных на квантовых явлениях. Необходимость в более эффективных алгоритмах и вычислительных подходах становится все более актуальной для преодоления этих ограничений и раскрытия полного потенциала квантовых симуляций.

Прямое моделирование эволюции квантовых состояний требует представления операторов временной эволюции, что становится крайне сложной задачей для систем, состоящих из большого числа частиц. В квантовой механике, состояние системы описывается волновой функцией, изменение которой во времени определяется уравнением Шрёдингера. Решение этого уравнения требует вычисления оператора временной эволюции $U(t)=e^{-iHt/\hslash }$, где $H$ — гамильтониан системы, а $\hslash$ — постоянная Планка. Однако, для сложных систем, гамильтониан представляет собой матрицу огромных размеров, и для представления и манипулирования этим оператором требуется экспоненциально растущий объем вычислительных ресурсов и памяти. Таким образом, даже при наличии мощнейших компьютеров, точное моделирование эволюции квантовых состояний для реалистичных материалов или молекул быстро становится невозможным, что обуславливает необходимость разработки приближенных методов и алгоритмов.

Для достижения практической применимости квантовых симуляций, неизбежно прибегают к различным приближениям. Эти методы, хотя и позволяют существенно снизить вычислительные затраты, вносят определенные погрешности в результаты. Степень этих ошибок может варьироваться в зависимости от выбранного приближения и сложности исследуемой системы. Например, использование методов теории возмущений или вариационных принципов может привести к неточным оценкам энергии и других свойств вещества. Тщательный анализ и контроль этих ошибок — критически важная задача, определяющая надежность и достоверность получаемых результатов, а также возможность корректной интерпретации полученных данных и их использования в дальнейших исследованиях, таких как разработка новых материалов или лекарственных препаратов. Оценка этих погрешностей часто требует проведения дополнительных вычислений или экспериментальной проверки, что усложняет процесс симуляции, но является необходимым для обеспечения научной строгости.

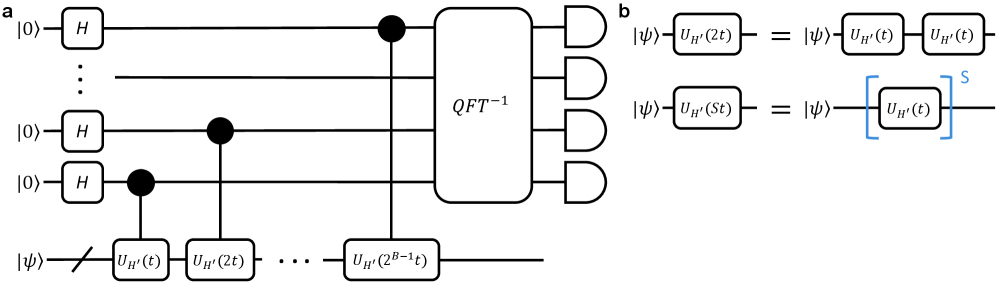
Разложение Троттера и Природа Ошибки

Разложение Троттера является широко используемым методом аппроксимации временной эволюции в квантовых вычислениях и моделировании. Суть метода заключается в разбиении сложной операции временной эволюции, описываемой оператором $e^{-iHt}$, на последовательность более простых операций, каждая из которых может быть реализована с большей точностью. Вместо одного сложного шага, вычисляется произведение экспонент от отдельных слагаемых гамильтониана $H={\sum }_k{H}_k$, то есть $e^{-iHt}\approx {\prod }_k{e}^{-i{H}_{k}t/n}$, где $n$ — количество шагов разложения. Такой подход позволяет упростить реализацию алгоритмов, особенно для систем со сложными взаимодействиями, однако вносит погрешность, поскольку отдельные слагаемые гамильтониана, как правило, не коммутируют.

Разложение Троттера, используемое для аппроксимации временной эволюции, вносит погрешность, известную как $TrotterError$, из-за некоммутативности членов гамильтониана. Некоммутативность означает, что порядок применения операторов, соответствующих различным членам гамильтониана, влияет на конечный результат. В частности, если гамильтониан имеет вид $H=H_1+H_2$, то $e^{-iHt}\ne e^{-i{H}_{1}t}{e}^{-i{H}_{2}t}$ в общем случае, что и приводит к появлению $TrotterError$ при аппроксимации $e^{-iHt}$ произведением экспонент операторов $H_1$ и $H_2$. Величина этой ошибки зависит от величины временного шага и характера некоммутативности между членами гамильтониана.

Оценка и количественная оценка ошибки Троттера критически важны для определения достоверности результатов моделирования. Проведенные исследования продемонстрировали высокую точность моделирования масштабирования ошибки Троттера, подтвержденную коэффициентом детерминации $R^2$ в диапазоне от 0.9927 до 0.9996. Это указывает на сильную корреляцию между предсказанными и наблюдаемыми значениями ошибки, позволяя надежно оценивать погрешность численных методов, основанных на разложении Троттера, и обеспечивать точность получаемых результатов.

Контроль Ошибок и Оценка Необходимых Ресурсов

Оценка погрешности Троттера, осуществляемая с помощью $CommutatorBound$, представляет собой классический метод определения величины ошибки, возникающей при использовании разложения Троттера для аппроксимации эволюции во времени в кванoвых симуляциях. Данный подход позволяет оценить максимальную разницу между точной эволюцией унитарного оператора и его аппроксимацией, что необходимо для разработки стратегий смягчения ошибок. $CommutatorBound$ вычисляется на основе коммутаторов операторов, составляющих разложение, и предоставляет верхнюю границу для $TrotterError$. Полученная оценка позволяет оценить точность симуляции и выбрать оптимальные параметры разложения для достижения требуемой точности с минимальными вычислительными затратами.

Оценка ресурсов — определение требований к количеству кубитов и числу логических вентилей — является критически важным этапом при реализации квантовых симуляций на реальном оборудовании. Этот процесс включает в себя анализ алгоритма для определения минимального количества кубитов, необходимых для кодирования квантового состояния, и подсчет общего числа операций, необходимых для выполнения симуляции. Точная оценка ресурсов необходима для проверки возможности реализации алгоритма на доступном оборудовании, а также для оптимизации алгоритма с целью снижения требований к ресурсам и повышения эффективности вычислений. Недооценка ресурсов может привести к невозможности реализации алгоритма, а переоценка — к неэффективному использованию аппаратных средств.

Оценка требуемых ресурсов — количества кубитов и операций — позволяет оптимизировать квантовые симуляции для конкретного аппаратного обеспечения. Тщательное балансирование между точностью вычислений и вычислительными затратами посредством $ResourceEstimation$ позволяет существенно снизить потребность в ресурсах. Для систем, состоящих из 100 кубитов, оптимизация может привести к снижению оценок требуемых ресурсов на 2-3 порядка величины, что делает реализацию более сложных квантовых алгоритмов практически осуществимой на существующих и перспективных квантовых устройствах.

Квантовое Превосходство и Перспективы Развития

Точное моделирование гамильтонианов, осуществляемое с помощью таких методов, как квантовая фазовая оценка, является фундаментальным строительным блоком для достижения квантового превосходства. Этот подход позволяет эффективно вычислять собственные значения и собственные векторы квантовых систем, что критически важно для решения сложных задач в химии, материаловедении и физике элементарных частиц. Суть метода заключается в преобразовании исходной задачи в более простую, которую можно эффективно решить на квантовом компьютере, используя интерференцию квантовых состояний для извлечения необходимой информации о спектре гамильтониана. Успешная реализация точного $HamiltonianSimulation$ открывает путь к решению проблем, недоступных классическим вычислительным ресурсам, и демонстрирует потенциал квантовых компьютеров для революционных научных открытий.

Для обеспечения надежности и объективности результатов квантового моделирования широко используется тестирование на случайных гамильтонианах Паули. Этот подход позволяет создать набор задач, для которых не существует известных классических решений, и сравнить производительность квантовых и классических алгоритмов. Использование случайных гамильтонианов Паули гарантирует, что результаты не будут искажены специфическими свойствами конкретной задачи, а отражают общую вычислительную мощность используемой квантовой системы. Такое тестирование является ключевым этапом в подтверждении достижения квантового превосходства, поскольку позволяет убедиться, что квантовый компьютер действительно решает задачи, недоступные для классических машин, и что полученные результаты соответствуют теоретическим предсказаниям. Оценка производительности на случайных гамильтонианах Паули предоставляет надежную основу для сравнения различных квантовых платформ и алгоритмов, способствуя дальнейшему развитию квантовых вычислений.

Развитие квантовых вычислений, в частности, создание машин нового поколения, таких как $MegaQuopMachine$, с увеличенным числом кубитов и повышенной когерентностью, открывает новые горизонты для моделирования сложных систем. Проведенные исследования демонстрируют возможность достижения относительной погрешности в оценке фазы на уровне 0.16% при использовании 1000 случайно сгенерированных состояний. Для превышения наихудшей ошибки фазы требуется от $10^3$ до $10^7$ выборок, при этом необходимое количество зависит от размера моделируемой системы. Эти результаты указывают на перспективность увеличения масштаба квантовых симуляций и приближение к решению задач, недоступных классическим компьютерам.

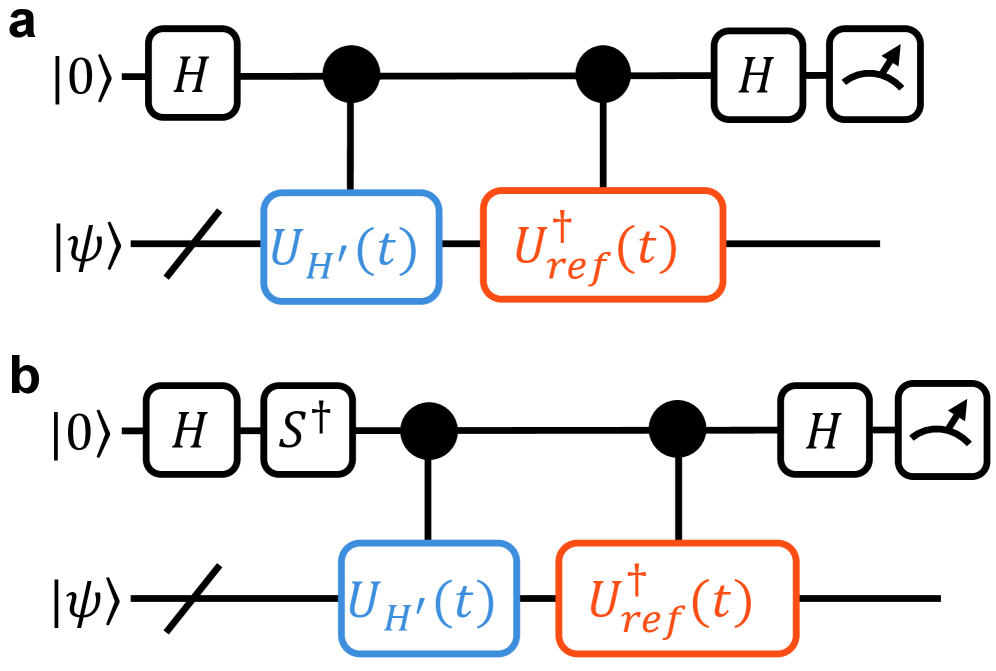
Исследование, представленное в данной работе, фокусируется на точной оценке ресурсов, необходимых для квантовых алгоритмов, используя возможности небольших квантовых компьютеров для вычисления ошибок симуляции. Этот подход позволяет не только оптимизировать процесс разработки алгоритмов, но и потенциально достичь квантического преимущества в самой оценке ресурсов. Как заметил Луи де Бройль: «Каждый фотон, каждая частица несет в себе информацию о вселенной». Подобно тому, как квантовые частицы несут информацию, квантовые вычисления, посредством точной оценки ошибок, раскрывают информацию о возможностях и ограничениях квантовых систем, открывая путь к более эффективным и мощным алгоритмам.

Куда же дальше?

Представленная работа, хотя и демонстрирует перспективный подход к оценке ресурсов для квантовых алгоритмов, лишь слегка приоткрывает завесу над истинной сложностью задачи. Точность оценки, полученная на малых квантовых устройствах, является лишь первым шагом. Очевидно, что экстраполяция этих данных на масштабируемые системы сопряжена с риском, особенно учитывая нелинейную природу накопления ошибок. Каждое отклонение в экспериментальных данных, каждое «выброс», представляет собой потенциальную возможность выявить скрытые зависимости, которые упускаются из виду при упрощенном моделировании.

Особый интерес представляет изучение влияния различных стратегий смягчения ошибок на точность оценки ресурсов. Необходимо тщательно исследовать, как методы коррекции и смягчения ошибок, эффективные на текущих NISQ-устройствах, будут масштабироваться с увеличением числа кубитов и глубины цепей. Вероятно, ключ к достижению квантового преимущества в оценке ресурсов лежит не только в совершенствовании алгоритмов, но и в разработке новых, более устойчивых к ошибкам архитектур.

В конечном счете, представленная методология должна быть расширена для охвата более широкого спектра квантовых алгоритмов и задач. Понимание закономерностей, управляющих потреблением ресурсов, требует систематического анализа различных алгоритмических подходов и их чувствительности к ошибкам. Именно в этом кроется путь к созданию квантовых систем, способных не только решать сложные задачи, но и точно оценивать стоимость этого решения.

---

Оригинал статьи: https://arxiv.org/pdf/2512.02131.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/