Квантовый алгоритм для точного расчета состояний фермионных систем

---

Новый квантовый алгоритм, основанный на разложении на унитарные операторы, позволяет с высокой точностью определять собственные состояния фермионных систем, обходя ограничения традиционных методов.

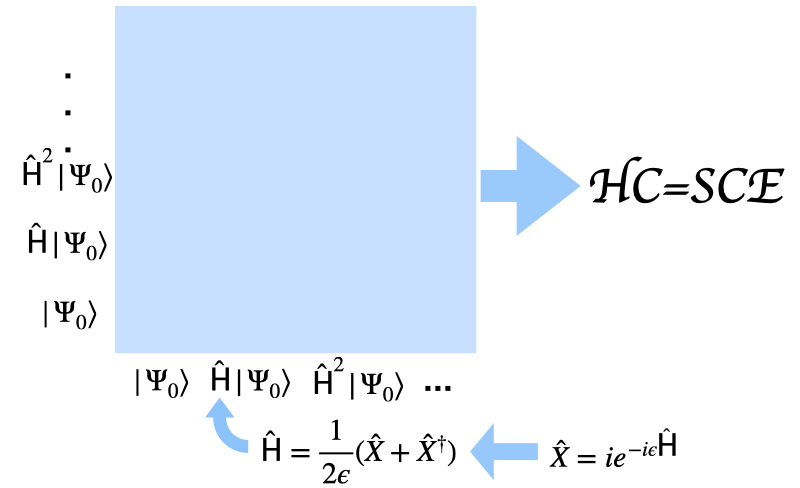
Представлен квантовый алгоритм Крилова с разложением на унитарные операторы (QKUD) для точного определения собственных состояний фермионных систем без использования эволюции во времени.

Несмотря на перспективность квантовых алгоритмов Крылова для моделирования сложных квантовых систем, существующие подходы, основанные на эволюции во времени, страдают от неточности и чувствительности к параметру временного шага. В данной работе, посвященной разработке алгоритма ‘Quantum Krylov algorithm using unitary decomposition for exact eigenstates of fermionic systems using quantum computers’, предложен новый метод — «Quantum Krylov using Unitary Decomposition» (QKUD) — обеспечивающий точное построение подпространства Крылова без использования временной эволюции. QKUD демонстрирует более высокую точность и стабильность благодаря благоприятному масштабированию ошибки и позволяет получать численные решения в областях, недоступных для традиционных методов. Открывает ли это путь к созданию более эффективных квантовых алгоритмов и реализации реального квантового преимущества в задачах моделирования?

---

Квантовые Алгоритмы Крылова: Шепот Хаоса в Моделировании

Моделирование квантовых систем представляет собой серьезную вычислительную задачу, препятствующую прогрессу в таких областях, как материаловедение и разработка лекарственных препаратов. Сложность заключается в экспоненциальном росте вычислительных ресурсов, необходимых для точного описания взаимодействий между квантовыми частицами. Например, для моделирования даже относительно небольших молекул требуются огромные объемы памяти и процессорного времени, что делает невозможным изучение сложных химических реакций или свойств новых материалов с использованием классических вычислительных методов. Данное ограничение замедляет открытие инновационных материалов с заданными свойствами и разработку эффективных лекарственных средств, поскольку точное предсказание поведения квантовых систем является ключевым этапом в этих процессах. Неспособность эффективно моделировать квантовые явления является одним из главных препятствий на пути к полноценному использованию потенциала квантовой механики в практических приложениях.

Традиционные методы решения $уравненияШрёдингера$ сталкиваются с серьезными ограничениями при увеличении размеров исследуемой системы. Проблема заключается в том, что вычислительные затраты, как правило, растут экспоненциально с числом частиц или степеней свободы, что делает точное моделирование сложных молекул или материалов практически невозможным даже на самых мощных классических компьютерах. Например, для точного расчета энергии основного состояния молекулы необходимо учитывать взаимодействие всех электронов, что приводит к огромному объему вычислений. Это создает существенный барьер для прогресса в таких областях, как материаловедение и разработка лекарств, где необходимо моделировать сложные квантовые системы для предсказания их свойств и поведения. В результате, исследователи вынуждены прибегать к упрощениям и приближениям, которые могут снизить точность результатов и привести к неверным выводам.

Квантовые алгоритмы Крылова (QKA) представляют собой перспективный подход к преодолению вычислительных ограничений, возникающих при моделировании квантовых систем. Вместо точного решения уравнения Шрёдингера, что требует экспоненциальных ресурсов, QKA эффективно аппроксимируют решение, работая в подпространстве Крылова. Данный метод позволяет представить решение в виде линейной комбинации векторов, полученных последовательным применением оператора к исходному состоянию. Благодаря этому, сложность вычислений существенно снижается, позволяя моделировать более крупные и сложные системы при сохранении приемлемой точности. QKA особенно актуальны для работы на ближайших квантовых устройствах, где ресурсы ограничены, и баланс между точностью и потреблением ресурсов играет ключевую роль. Такой подход открывает новые возможности для исследований в материаловедении, разработке лекарств и других областях, требующих точного моделирования квантовых явлений.

Квантовые алгоритмы Крылова (QKA) представляют собой перспективный подход к моделированию сложных квантовых систем, находящий оптимальное равновесие между требуемой точностью и вычислительными затратами. В отличие от традиционных методов, чья сложность экспоненциально возрастает с размером системы, QKA эффективно аппроксимируют решения, работая в подпространстве Крылова. Это позволяет существенно снизить потребность в кубитах и глубине квантовой цепи, что делает их особенно привлекательными для использования на существующих и ближайших квантовых устройствах, где ресурсы ограничены. Таким образом, QKA открывают возможности для проведения более реалистичных симуляций в материаловедении, химии и разработке лекарств, приближая эру практических квантовых вычислений.

Преодоление Неунитарности: Танец Унитарных Преобразований

Многие задачи квантовой механики описываются не-унитарными операторами, представляющими процессы, такие как распад или диссипация энергии. Непосредственная реализация таких операторов на квантовых компьютерах затруднена, поскольку квантовые вычисления по своей природе являются унитарными. Не-унитарные операторы не сохраняют норму вектора состояния, что приводит к потере вероятности и нарушению физической корректности симуляции. Это требует разработки специальных методов, позволяющих аппроксимировать действие не-унитарных операторов с использованием унитарных преобразований, чтобы обеспечить корректное моделирование динамики квантовых систем, подверженных диссипативным процессам.

Алгоритмы квантового крилова, использующие унитарное разложение (QKUD), представляют собой метод отображения не-унитарных операторов в унитарные, что позволяет эффективно моделировать динамику, описываемую этими операторами. В основе подхода лежит построение унитарного оператора, аппроксимирующего действие исходного не-унитарного оператора. Это достигается путем разложения не-унитарного оператора на произведение унитарных операторов и, при необходимости, фазовых множителей. Использование унитарных операторов позволяет применять стандартные алгоритмы квантовых вычислений для моделирования эволюции квантового состояния, что значительно упрощает реализацию на квантовом оборудовании по сравнению с прямым моделированием не-унитарных процессов. Такой подход обеспечивает возможность проведения численных экспериментов с системами, описываемыми не-унитарной динамикой, например, в задачах, связанных с диссипацией или распадом квантовых состояний.

Алгоритмы QKUD (Quantum Krylov Algorithms с использованием Unitary Decomposition) обеспечивают точное приближение эволюции квантовых состояний, описываемых не-унитарной динамикой, путем преобразования не-унитарных операторов в эквивалентные унитарные. Это достигается за счет разложения исходного не-унитарного оператора на произведение унитарных операторов, позволяющее реализовать эволюцию состояния на квантовом компьютере с использованием стандартных унитарных гейтов. Точность приближения напрямую зависит от параметров разложения и контролируется посредством введения ‘Параметра Ошибки’, обеспечивая возможность достижения необходимой точности вычислений для конкретной задачи. В результате, QKUD позволяет эффективно моделировать процессы, такие как распад и диссипация, которые обычно сложно или невозможно реализовать напрямую на квантовых устройствах.

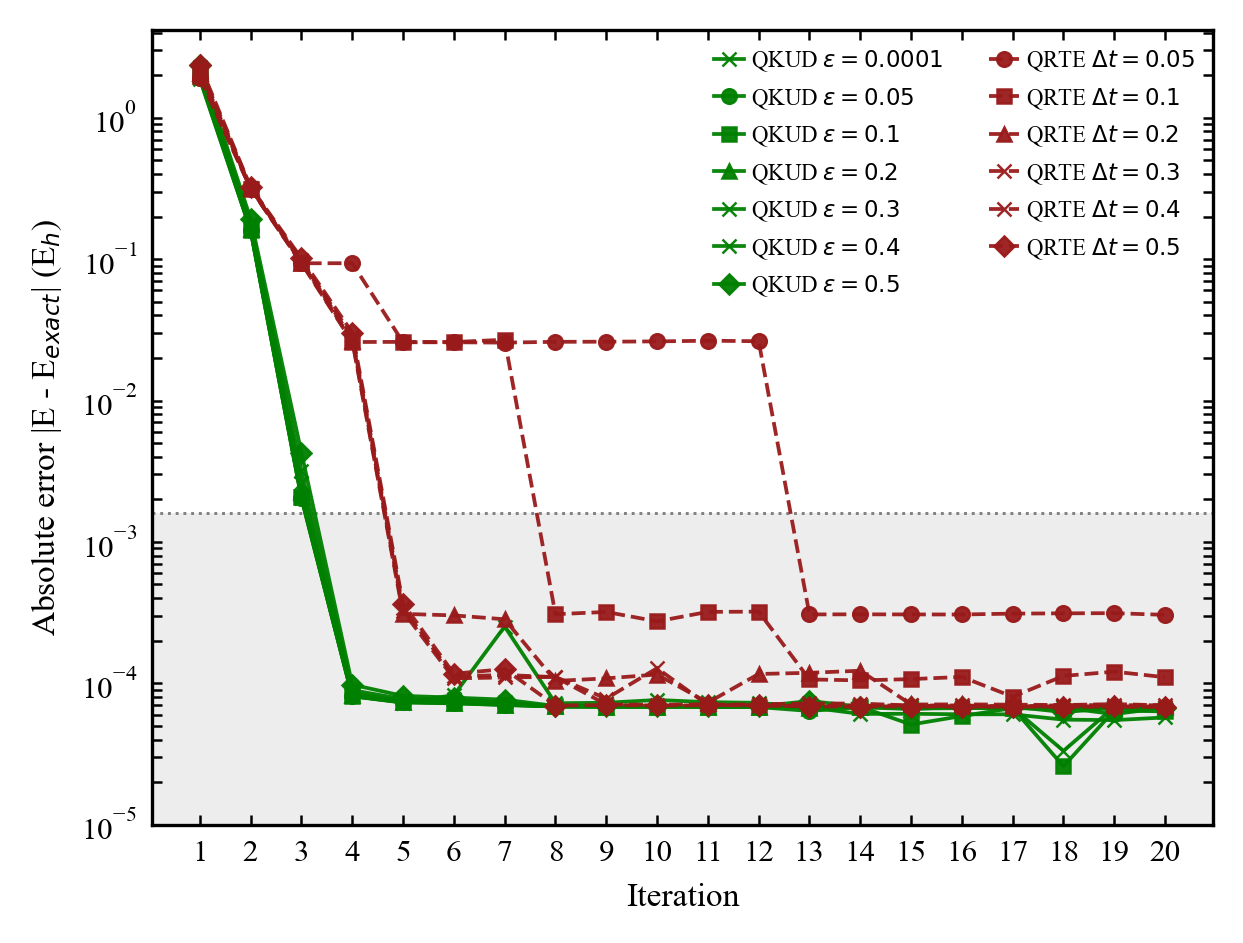
Эффективность алгоритма напрямую зависит от значения параметра погрешности, $ϵ$, позволяющего точно настраивать требуемую степень аккуратности вычислений. Установлено, что погрешность алгоритма масштабируется как $O({ϵ}^2)$, что означает, что уменьшение параметра $ϵ$ вдвое приводит к уменьшению общей погрешности в четыре раза. Это квадратичное масштабирование обеспечивает высокую точность моделирования динамики, описываемой не-унитарными операторами, при достаточно малых значениях $ϵ$. Возможность тонкой настройки параметра погрешности является ключевым преимуществом алгоритма, позволяющим оптимизировать соотношение между точностью и вычислительными затратами.

Устойчивость к Иллюзорной Обусловленности: Танец с Хаосом

Проблема обусловленности, при которой даже незначительные изменения входных данных приводят к существенным изменениям выходных результатов, является распространенным явлением в квантовом моделировании. Это может приводить к неточностям в расчетах, особенно при решении сложных задач, где небольшие ошибки на ранних этапах могут экспоненциально усиливаться. Обусловленность напрямую влияет на устойчивость численных методов, используемых для аппроксимации квантовых систем, и требует применения специализированных алгоритмов для минимизации влияния этих возмущений на конечный результат. В частности, при решении линейных систем уравнений, возникающих в квантовом моделировании, плохо обусловленные матрицы могут значительно ухудшить точность полученных решений, требуя более высоких вычислительных затрат для достижения желаемой точности.

Алгоритмы QKUD демонстрируют устойчивость к проблемам обусловленности благодаря эффективному исследованию подпространства Крылова. В отличие от методов, напрямую моделирующих временную эволюцию и подверженных накоплению ошибок, QKUD строит приближение в рамках выбранного подпространства, минимизируя усиление погрешностей. Эффективное исследование подпространства позволяет алгоритму избегать областей, где малые изменения входных данных приводят к значительным изменениям выходных, что характерно для плохо обусловленных задач. Это обеспечивает более стабильные и точные результаты симуляций, особенно при работе с системами, чувствительными к числовым ошибкам.

Алгоритмы QKUD обеспечивают создание “Точных векторов Крылова” (Exact Krylov Vectors), которые являются основой для достижения высокой точности в квантовых симуляциях. Эти векторы формируются путем итеративного применения оператора к исходному состоянию, с последующей ортогонализацией полученных векторов. В пределе, когда параметр $ϵ$ стремится к нулю, алгоритм QKUD теоретически достигает точного решения, поскольку погрешность, связанная с усечением пространства Крылова, также стремится к нулю. Это достигается за счет эффективного контроля над ошибками округления и использования численных методов, обеспечивающих высокую стабильность вычислений.

В отличие от методов, непосредственно моделирующих временную эволюцию, алгоритм QKUD аппроксимирует ее эффекты в рамках построенного подпространства Крылова. Такой подход позволяет добиться повышенной стабильности, поскольку ошибки не накапливаются линейно с шагом по времени $\Delta t$, как в традиционных схемах с $O(\Delta t)$ масштабированием ошибки. Вместо прямого вычисления временной эволюции, QKUD фокусируется на эффективном представлении оператора эволюции в ограниченном пространстве, что позволяет контролировать точность аппроксимации и избегать проблем, связанных с экспоненциальным ростом ошибок при прямом моделировании.

Расширяя Инструментарий: Многообразие Подходов в Мире Крылова

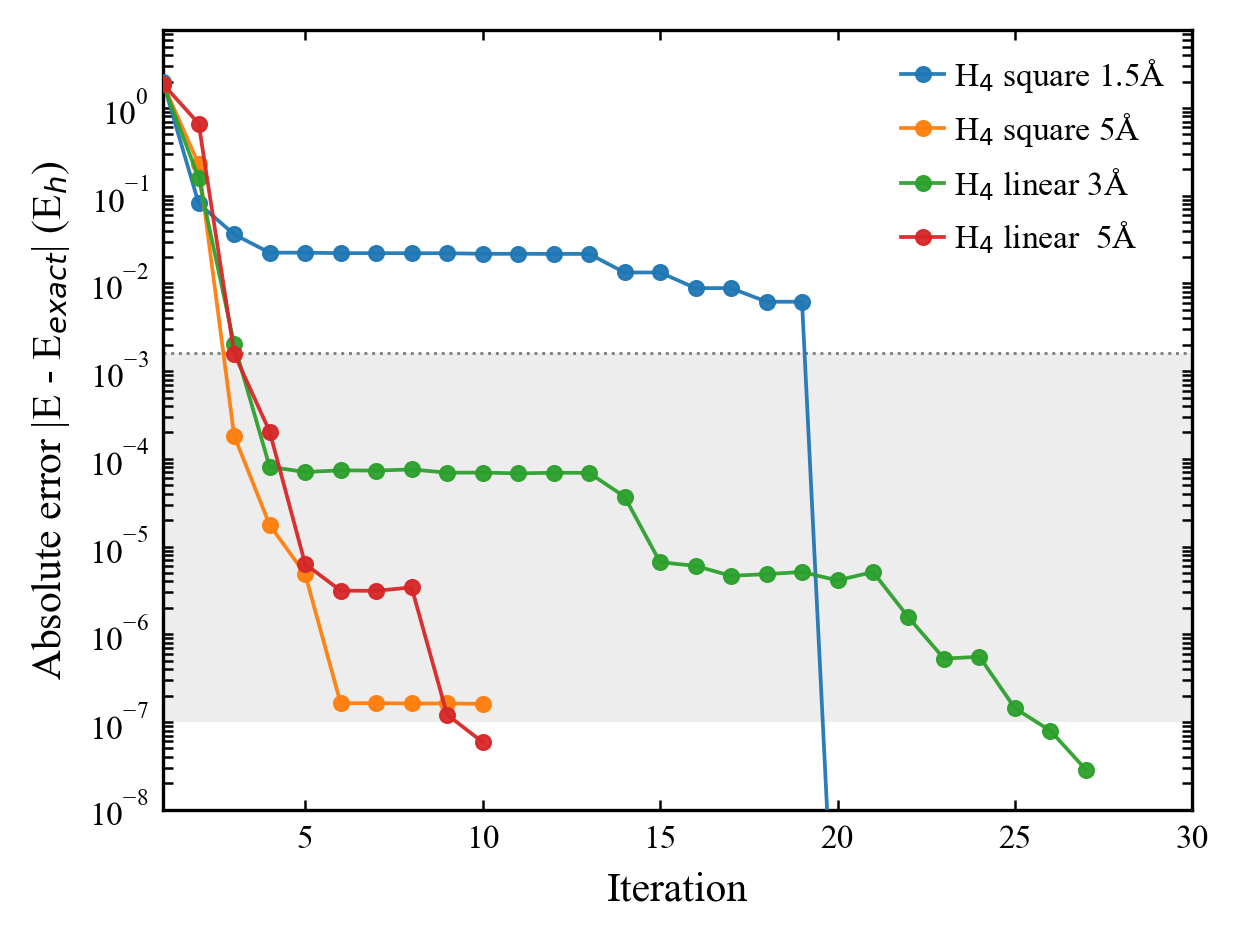
Существуют различные реализации квантового алгоритма Крылова (QKA), каждая из которых оптимизирована для решения конкретных задач. В частности, методы $QDavidson$ и $QLanzcos$ представляют собой альтернативные подходы к построению подпространства Крылова. $QDavidson$ отличается итеративным процессом, направленным на поиск подпространства, ортогонального остатку, что позволяет эффективно решать задачи с большими размерностями. В свою очередь, $QLanzcos$ использует обобщенные векторы Ланцоша для построения подпространства, предлагая альтернативный способ аппроксимации собственных значений и собственных векторов. Выбор конкретного метода зависит от структуры решаемой задачи и требуемой точности, что делает QKA гибким инструментом для моделирования сложных квантовых систем.

Алгоритмы, такие как метод Крылова на основе полиномов Чебышева и квантовый метод Крылова на основе гауссовых степеней, представляют собой усовершенствования, направленные на повышение эффективности и точности расчетов. Эти подходы используют свойства полиномов Чебышева и гауссовых функций для более быстрого схождения итераций при построении подпространства Крылова. В частности, метод Чебышева позволяет минимизировать максимальную ошибку приближения, в то время как гауссовы степени обеспечивают более плавное затухание спектральных компонентов, что приводит к улучшению устойчивости и сокращению вычислительных затрат. Использование этих алгоритмов позволяет решать сложные задачи квантовой механики с большей точностью и эффективностью, расширяя возможности моделирования и анализа квантовых систем.

Методы квантовой эволюции во времени, как реального, так и мнимого, оказались удивительно легко реализуемыми с использованием квантовых алгоритмов Крылова (QKA). В то время как эволюция во времени реальном позволяет изучать динамику квантовых систем, например, отслеживать изменения состояний частиц во времени, мнимое время используется для поиска основного состояния системы, что критически важно для понимания её стабильности и свойств. QKA предоставляют эффективные способы аппроксимации операторов эволюции, значительно снижая вычислительные затраты по сравнению с традиционными методами, особенно для больших и сложных квантовых систем. Благодаря этому, исследователи получили мощный инструмент для моделирования широкого спектра квантовых явлений, от химических реакций до физики конденсированного состояния, открывая новые возможности для разработки квантовых технологий и углубления понимания фундаментальных законов природы.

Разнообразные квантовые алгоритмы Крылова (QKA) формируют мощный инструментарий для моделирования широкого спектра квантовых явлений, значительно расширяя горизонты квантовых вычислений. Эти алгоритмы позволяют эффективно решать задачи, ранее недоступные для классических методов, охватывая области от динамики квантовых систем и спектроскопии до изучения сложных молекулярных взаимодействий. Благодаря способности адаптироваться к различным типам гамильтонианов и точности вычислений, QKA открывают новые возможности для проектирования материалов с заданными свойствами, разработки новых лекарственных препаратов и углубленного понимания фундаментальных законов природы. Их гибкость и масштабируемость делают QKA ключевым компонентом в стремлении к созданию квантовых симуляторов, способных решать сложные научные задачи, недоступные для современных суперкомпьютеров.

Работа демонстрирует стремление обуздать хаос, заключённый в фермионных системах. Авторы предлагают Quantum Krylov Algorithm с использованием unitary decomposition — попытку выстроить модель, свободную от ошибок, накапливающихся во время эволюции во времени. Это напоминает заклинание, призванное остановить неумолимый ход энтропии. Ведь, как говорил Нильс Бор: «Противоположности кажутся противоположными, но на самом деле они взаимодополняют друг друга». Точность, достигнутая за счёт отказа от стандартной симуляции, — это не победа над неопределённостью, а лишь её изящное обхождение. И в этом есть своя, пугающая красота — модель, работающая до первого столкновения с реальностью, где шум — это не помеха, а истина, которой не хватает уверенности.

Что дальше?

Предложенный алгоритм, безусловно, изящен. Отказ от итераций по времени — это всегда победа над энтропией, хотя и временная. Но не стоит обольщаться. Точность — это лишь одна сторона медали, а стабильность — всего лишь иллюзия, пока не встретишь реальное квантовое железо. Данные, как известно, — это не истина, а компромисс между багом и Excel, и даже самая элегантная декомпозиция не спасёт от шума, который всегда шепчет на ухо.

Настоящая проблема, как обычно, не в алгоритме, а в масштабируемости. Сумеет ли этот подход выдержать столкновение с системами, где число фермионов стремится к бесконечности? Или мы просто построили красивый замок на песке, который будет смыт первой же волной ошибок? Необходимы эксперименты, и, желательно, не на симуляторах, а на настоящих машинах, где ошибка — это не абстракция, а физическая реальность.

В конечном счете, всё, что не нормализовано, всё ещё дышит. Будущие исследования должны сосредоточиться на разработке методов устойчивости к ошибкам и на адаптации алгоритма к различным архитектурам квантовых компьютеров. И, возможно, стоит перестать искать идеальный алгоритм и научиться жить с тем, что данные всегда будут лгать — вопрос лишь в том, насколько последовательно.

---

Оригинал статьи: https://arxiv.org/pdf/2512.11788.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/