Квантовый отклик под контролем: Анализ памяти системы

---

Новая работа предлагает всесторонний теоретический подход к управлению открытыми квантовыми системами, фокусируясь на статистике функций памяти, определяющих динамику систем.

Исследование посвящено свойствам функций памяти, используемых в стратегиях квантной обратной связи и их влиянию на динамику гибридных классическо-квантовых систем.

Несмотря на значительный прогресс в управлении квантовыми системами, эффективное использование информации, полученной в процессе измерений, остается сложной задачей. В данной работе, ‘Deterministic Equations for Feedback Control of Open Quantum Systems II: Properties of the memory function’, представлен всесторонний теоретический подход к анализу квантового обратного управления, фокусирующийся на статистических свойствах функций памяти, используемых для обработки результатов измерений и влияния на динамику системы. Показано, что функцию памяти можно рассматривать как классическую систему, взаимодействующую с квантовой системой, что позволяет ввести информационно-теоретические меры корреляций между ними. Открывает ли предложенный формализм новые возможности для разработки оптимальных стратегий обратной связи и повышения устойчивости квантовых систем к шуму и диссипации?

---

Квантовая неопределенность: Вызов традиционному контролю

Квантовые системы представляют собой сложнейшую задачу для управления, поскольку их состояние крайне чувствительно к малейшим возмущениям окружающей среды и внутренним динамическим процессам. Даже незначительные флуктуации температуры, электромагнитные поля или механические вибрации могут привести к декогеренции — потере квантовой информации и разрушению хрупкого состояния суперпозиции. Эта восприимчивость к шуму требует разработки специальных методов контроля, способных компенсировать внешние воздействия и поддерживать когерентность квантовых состояний на достаточно длительное время для выполнения вычислительных операций или передачи информации. Более того, собственная динамика квантовых систем, определяемая $Schr\ddot{o}dinger$ уравнением, добавляет сложности, поскольку управление должно учитывать естественное развитие системы во времени, а не просто пытаться ее “остановить” или изменить.

Традиционные методы управления квантовыми системами сталкиваются с существенными трудностями в поддержании когерентности и достижении точной манипуляции квантовыми состояниями. Дело в том, что квантовые состояния чрезвычайно чувствительны к любым внешним возмущениям, что приводит к быстрой декогеренции — потере квантовой информации. Попытки использовать классические методы управления, основанные на точном задании параметров, часто терпят неудачу из-за непредсказуемости квантовой динамики и невозможности полностью изолировать систему от окружения. Удержание квантовой информации требует борьбы с этим постоянным «шумом», что затрудняет реализацию сложных квантовых алгоритмов и разработку надежных квантовых технологий. Сохранение $T_2$ — времени декогеренции — является ключевой задачей, определяющей возможности управления и масштабируемости квантовых систем.

Ограничения традиционного, так называемого разомкнутого управления, в квантовых системах обусловлены их исключительной чувствительностью к внешним возмущениям и внутренним динамическим процессам. В отличие от классических систем, где можно точно задать параметры и получить предсказуемый результат, квантовые состояния легко разрушаются даже незначительными флуктуациями окружающей среды. Поэтому возникает потребность в разработке инновационных стратегий управления, способных компенсировать эти нежелательные эффекты и поддерживать когерентность квантовых состояний на достаточно длительное время. Стремление к созданию устойчивых и надежных квантовых технологий, способных функционировать в реальных условиях, диктует необходимость перехода от простых методов управления к сложным алгоритмам, использующим обратную связь и адаптивное управление для минимизации ошибок и обеспечения высокой точности манипуляций с кубитами. Эти усовершенствованные подходы открывают путь к практическому применению квантовых вычислений, связи и сенсорики.

Обратная связь как квантовый стабилизатор: Новый подход

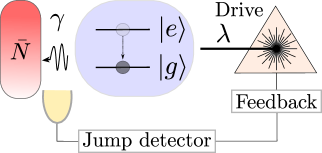
Реализация обратной связи в квантовых системах требует непрерывного мониторинга состояния системы посредством методов, таких как регистрация квантовых скачков. Данный процесс включает в себя последовательные измерения, позволяющие определить, произошло ли изменение в квантовом состоянии системы. Обнаружение квантовых скачков основывается на анализе слабого сигнала, указывающего на переход системы из одного состояния в другое, что позволяет получить информацию о динамике системы в реальном времени. Частота и характеристики этих скачков напрямую связаны с параметрами системы и факторами, вызывающими декогеренцию, что делает данный метод ключевым для стабилизации квантового состояния и поддержания когерентности.

Полученные данные измерений состояния квантовой системы используются для формирования корректирующих сигналов, направленных на компенсацию эффектов декогеренции. Эти сигналы, реализованные посредством точного управления параметрами системы, позволяют стабилизировать квантовое состояние, минимизируя потери квантовой информации. Эффективность стабилизации напрямую зависит от скорости обработки данных измерений и точности применяемых корректирующих воздействий, определяемых спецификой конкретной квантовой системы и механизмом декогеренции. При этом, корректирующие сигналы могут быть реализованы как в виде мгновенных импульсов, так и в виде непрерывных поправок к управляющим параметрам, в зависимости от характера и скорости процессов декогеренции.

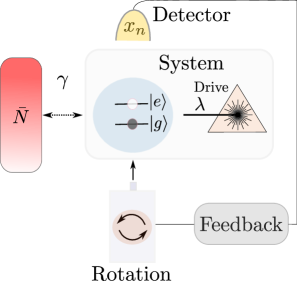
В основе данного подхода лежит гибридная классическо-квантовая система, в которой классические вычисления обрабатывают результаты измерений, полученные от квантовой системы. Эти результаты служат входными данными для алгоритмов классической обработки, генерирующих корректирующие сигналы. Сгенерированные сигналы, в свою очередь, используются для управления состоянием квантовой системы, реализуя обратную связь и стабилизируя её против декогеренции. Таким образом, классический вычислительный блок выполняет роль контроллера, интерпретируя квантовые измерения и определяя необходимые действия для поддержания стабильности квантовой системы, обеспечивая непрерывный цикл измерения-обработки-коррекции.

Применение методов $ProjectiveMeasurement$ и $ContinuousMonitoring$ обеспечивает детализированное представление о квантовом состоянии системы. $ProjectiveMeasurement$ позволяет определить вероятность нахождения системы в конкретном состоянии при каждом измерении, предоставляя дискретные значения. В свою очередь, $ContinuousMonitoring$ осуществляет постоянное наблюдение за системой, регистрируя изменения ее параметров во времени и предоставляя непрерывный поток данных. Комбинация этих подходов позволяет не только определить текущее состояние, но и отследить динамику его эволюции, что критически важно для реализации эффективной обратной связи и стабилизации квантовой системы против декогеренции. Данные методы позволяют выявить слабые сигналы и отклонения, которые могли бы остаться незамеченными при использовании менее чувствительных методов измерения.

Количественная оценка управления: Взаимная информация и динамика системы

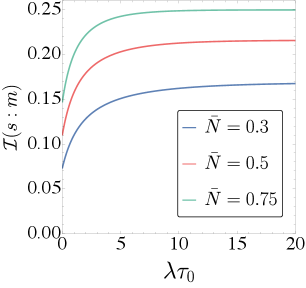
Эффективность обратной связи в управлении квантовой системой напрямую связана с объемом информации, полученной о системе в результате измерения и сохраненной в классической памяти, который количественно оценивается с помощью $ВзаимнойИнформации$ (Mutual Information). Этот показатель отражает уменьшение неопределенности в состоянии квантовой системы после каждого измерения и обновления классической памяти. Более высокие значения $ВзаимнойИнформации$ указывают на более эффективное подавление декогеренции и стабилизацию состояния системы, что свидетельствует о лучшей работе стратегии управления. Таким образом, $ВзаимнаяИнформация$ служит ключевым метриком для оценки эффективности обратной связи и оптимизации параметров управления квантовой системой.

Количество информации, измеряемое с помощью $MutualInformation$, служит количественной метрикой для оценки эффективности стратегии управления. Наблюдаемое увеличение значений $MutualInformation$ в стабилизированных системах напрямую коррелирует с улучшением контроля над квантовым состоянием. Это позволяет сравнивать различные стратегии управления, выбирая ту, которая обеспечивает максимальный прирост информации о системе и, следовательно, обеспечивает наиболее стабильное и предсказуемое поведение. Таким образом, $MutualInformation$ предоставляет объективный критерий для оптимизации протоколов обратной связи и оценки их производительности в задачах квантового управления.

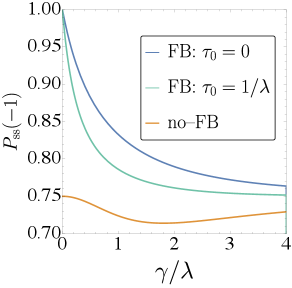
Анализ долгосрочного поведения системы с использованием метода $SteadyStateAnalysis$ позволяет оценить стабильность и эффективность контура обратной связи. Данный метод предполагает вычисление стационарного распределения вероятностей состояния системы после установления обратной связи. Полученное стационарное состояние характеризуется минимальной энергией и определяет пределы, в которых система будет оставаться при воздействии шума и возмущений. Отклонение от стационарного состояния указывает на нестабильность системы или недостаточную эффективность алгоритма управления. Количественная оценка стационарного состояния, включающая средние значения операторов и их флуктуации, предоставляет метрики для сравнения различных стратегий обратной связи и оптимизации параметров управления.

Анализ ковариации между операторами Паули и классической памятью системы показывает отрицательную корреляцию. Это указывает на то, что каждое детектирование скачка (jump detection) в процессе обратной связи способствует перемещению квантовой системы в направлении основного состояния (ground state). Измерение ковариации позволяет количественно оценить, насколько эффективно обратная связь направляет систему к состоянию с минимальной энергией, и демонстрирует тенденцию к уменьшению отклонений от этого состояния с каждым циклом измерения и коррекции.

Использование $DeterministicEquation$ позволяет построить модель процесса обратной связи и предсказать эволюцию системы. Анализ показывает, что $Two-PointCorrelationFunction$ (функция корреляции по двум точкам) уменьшается с увеличением временных интервалов и интенсивности обратной связи. Данное снижение корреляции указывает на то, что информация о состоянии системы со временем теряется, что является ожидаемым результатом эффективной обратной связи, стремящейся к стабилизации и уменьшению неопределенности. Модель позволяет количественно оценить скорость этого уменьшения и оптимизировать параметры обратной связи для достижения максимальной эффективности.

Настройка квантовых состояний: Мощь инверсионных протоколов

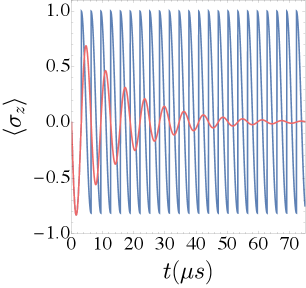
Разрабатываются специализированные протоколы обратной связи, такие как протокол $InversionProtocol$, позволяющие целенаправленно изменять квантовое состояние системы. В частности, подобные протоколы способны инвертировать популяцию кубита, то есть перевести его из основного состояния в возбужденное, и наоборот. Этот процесс требует точного контроля над квантовой системой и предполагает использование обратной связи для поддержания желаемого состояния, несмотря на естественные процессы релаксации и декогеренции. Возможность манипулирования популяцией кубитов открывает широкие перспективы для создания более эффективных и стабильных квантовых устройств и алгоритмов.

Протоколы управления квантовыми состояниями активно используют непрерывные циклы обратной связи для компенсации естественных процессов распада, таких как $ThermalDecay$. Данные процессы, неизбежно приводящие к переходу системы в основное состояние, эффективно подавляются посредством постоянного мониторинга и корректировки параметров квантовой системы. В результате, становится возможным поддерживать желаемое возбужденное состояние в течение продолжительного времени, что критически важно для реализации сложных квантовых операций и поддержания когерентности. Именно непрерывный характер обратной связи позволяет системе противодействовать энтропии и сохранять информацию, закодированную в квантовом состоянии.

Эффективность протокола инверсии напрямую зависит от точности обратной связи и контроля над управляющими сигналами. Любые отклонения в процессе измерения состояния кубита и последующей коррекции, вызванные шумами или несовершенством измерительной аппаратуры, приводят к накоплению ошибок и снижению вероятности успешного перевода системы в желаемое состояние. Высокоточная обратная связь, способная оперативно реагировать на флуктуации и компенсировать естественные процессы релаксации, такие как $T_1$ и $T_2$ декогеренция, является критически важной для поддержания когерентности и достижения высокой верности инверсии. Точность управляющих импульсов, определяющая скорость и селективность манипуляций с кубитом, также играет ключевую роль в минимизации ошибок и оптимизации протокола.

Успешная реализация протоколов управления квантовыми состояниями, таких как инверсионные протоколы, открывает перспективы для создания принципиально новых квантовых технологий. Способность эффективно поддерживать и манипулировать квантовыми состояниями, преодолевая естественные процессы декогеренции и релаксации, является ключевым требованием для разработки стабильных и масштабируемых квантовых вычислений. Это позволяет создавать кубиты с высокой степенью когерентности, необходимые для выполнения сложных квантовых алгоритмов. Кроме того, подобные протоколы могут быть использованы в квантовой сенсорике, обеспечивая беспрецедентную точность измерений, и в квантовой коммуникации, позволяя создавать защищенные каналы связи, не подверженные перехвату. В перспективе, освоение данных технологий позволит создать квантовые устройства, превосходящие возможности классических аналогов в широком спектре приложений, от медицины и материаловедения до финансов и искусственного интеллекта.

Представленная работа демонстрирует стремление к математической строгости в анализе квантовых систем управления. Особое внимание уделяется характеристике функций памяти, определяющих статистику обратной связи и влияющих на динамику системы. Это соответствует принципу, что корректность алгоритма должна быть доказуема, а не полагаться на эмпирические наблюдения. Как однажды заметил Вернер Гейзенберг: «Самое важное — это не знать». Это кажется парадоксальным, однако, в контексте квантовой механики, незнание точного состояния системы требует разработки методов, основанных на вероятностных характеристиках, что и реализовано в данной работе через анализ функций памяти и статистики обратной связи. Строгость математического подхода позволяет выйти за рамки простых тестов и обеспечить надежность управления квантовыми системами.

Куда Ведет Этот Путь?

Представленная работа, тщательно анализируя статистические свойства функции памяти в системах квантной обратной связи, неизбежно наталкивает на вопрос о границах применимости столь детального подхода. Увлечение точным описанием статистики, хотя и элегантно с математической точки зрения, не должно заслонять фундаментальную проблему: насколько вообще возможно достоверно моделировать сложные квантовые системы, подверженные неконтролируемым возмущениям? Попытки учесть все факторы, пусть и с помощью изящных математических конструкций, рискуют превратиться в бесконечную регрессию, лишь отодвигая неизбежное столкновение с реальностью несовершенства моделей.

Очевидным направлением дальнейших исследований представляется отказ от чрезмерной детализации в пользу феноменологических подходов. Вместо того чтобы стремиться к абсолютно точному описанию функции памяти, возможно, стоит сосредоточиться на идентификации ключевых параметров, определяющих эффективность стратегии обратной связи. Это потребует от исследователей готовности к компромиссам — признанию того, что эвристики, хотя и не обладают математической строгостью, могут оказаться более практичными в условиях ограниченных ресурсов и неполной информации.

В конечном счете, истинный прогресс в области квантового управления обратной связью, вероятно, будет достигнут не за счет усложнения математических моделей, а за счет развития более эффективных методов экспериментальной верификации и адаптации алгоритмов к реальным условиям. Иными словами, необходимо сместить акцент с теоретической чистоты на практическую целесообразность, не забывая, однако, что элегантность решения — это не просто эстетическое предпочтение, а показатель его внутренней устойчивости и надежности.

---

Оригинал статьи: https://arxiv.org/pdf/2512.08085.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/