Отличить производную от шума: Классификация методов численного дифференцирования

---

В статье представлен всесторонний обзор методов численного дифференцирования, помогающий выбрать оптимальный подход для получения точных производных в различных условиях.

Предлагается систематизированная таксономия численных методов дифференцирования, учитывающая особенности данных и структуру задачи, включая методы автоматического дифференцирования, фильтры Калмана и спектральные методы.

Несмотря на фундаментальную роль дифференцирования в науке и технике, прямое измерение производных часто невозможно, требуя применения численных методов. В работе, озаглавленной ‘A Taxonomy of Numerical Differentiation Methods’, представлен всесторонний анализ различных алгоритмов численного дифференцирования, охватывающий широкий спектр подходов — от спектральных методов до фильтрации Кальмана. Авторы систематизируют эти методы, выделяя их сильные и слабые стороны в зависимости от характеристик данных и структуры задачи, и предлагают оптимальные стратегии для различных сценариев, включая обработку зашумленных данных. Какие новые возможности откроет дальнейшая разработка и адаптация этих методов для решения сложных задач моделирования и анализа в различных областях?

---

Вызов Точного Оценки Производных

Многие научные и инженерные задачи, от моделирования динамики сложных систем до анализа сигналов и управления процессами, требуют точного вычисления производных на основе дискретных, выборочных данных. Например, в задачах геофизики, для определения скорости изменения сейсмических волн, или в финансовых моделях, для оценки темпов изменения стоимости активов, производные служат ключевым инструментом. Точность этих вычислений напрямую влияет на достоверность полученных результатов и эффективность принимаемых решений. Таким образом, способность надежно оценивать производные из дискретизированных данных является фундаментальной потребностью в широком спектре научных и технологических дисциплин, определяя необходимость разработки и применения специализированных алгоритмов и методов.

Традиционные методы вычисления производных, такие как метод конечных разностей, зачастую демонстрируют чувствительность к шумам в данных и нерегулярному интервалу дискретизации. Это приводит к существенным погрешностям в оценке производной, особенно при анализе реальных данных, где идеальные условия редко встречаются. Например, при вычислении $\frac{dy}{dx}$ с использованием конечных разностей, даже небольшие отклонения в значениях $y$ или $x$ могут привести к значительному искажению результата. В случае нерегулярных интервалов, стандартные формулы конечных разностей становятся неприменимыми, требуя сложных интерполяций или аппроксимаций, которые сами по себе вносят дополнительную погрешность. Таким образом, для точного определения скорости изменения величины в условиях несовершенных данных, необходимы более устойчивые и адаптивные подходы.

Ограничения традиционных методов вычисления производных, таких как метод конечных разностей, диктуют необходимость разработки более устойчивых и адаптивных подходов. В условиях зашумленных данных или неравномерно расположенных отсчетов, стандартные алгоритмы часто демонстрируют значительные погрешности, что критично для многих научных и инженерных приложений. Поэтому, активно исследуются альтернативные методы, использующие, например, сглаживание данных, вейвлет-преобразования или методы, основанные на машинном обучении, для повышения точности и надежности оценки $\frac{dy}{dx}$. Эти новые подходы стремятся обеспечить более стабильные результаты даже при наличии значительных помех и нерегулярности в исходных данных, открывая возможности для более точного моделирования и анализа сложных систем.

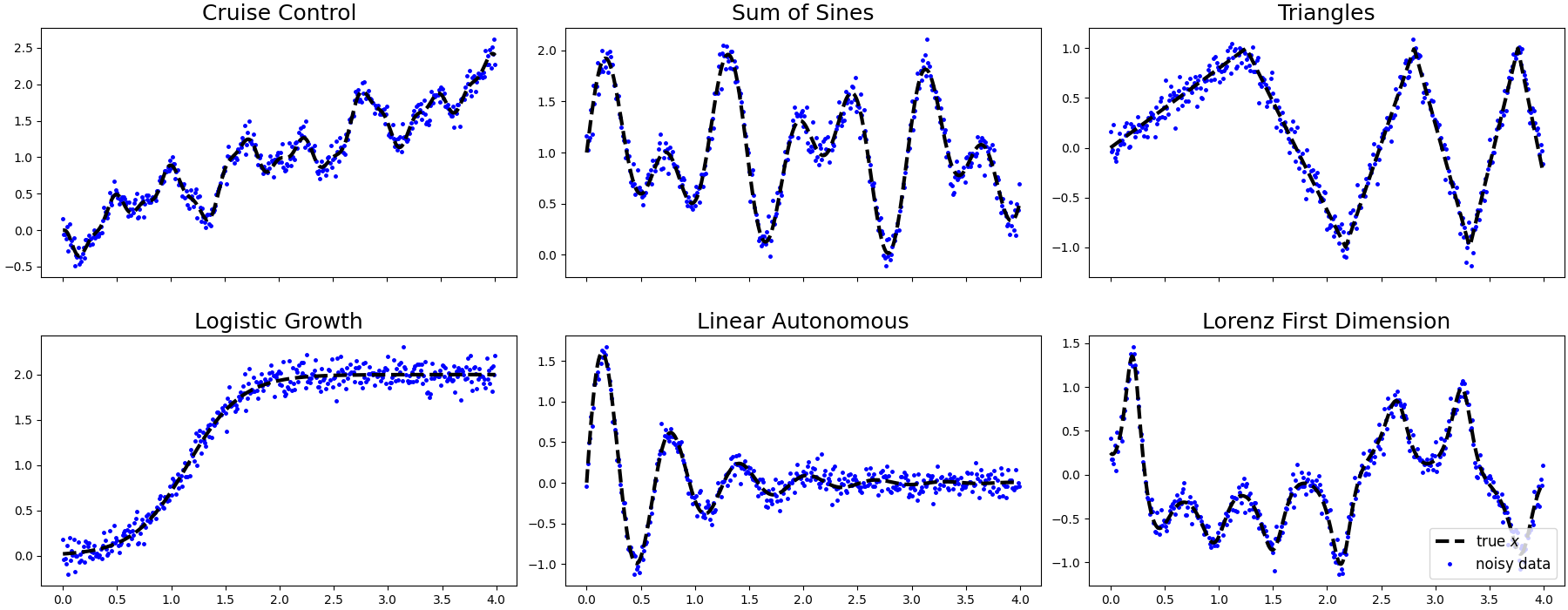
Рациональный Подход к Расчету Производных

Фреймворк функции потерь обеспечивает структурированный подход к оптимизации гиперпараметров при оценке производных, что критически важно при работе с зашумленными данными. В отличие от традиционных методов, которые часто полагаются на эвристические настройки, данный подход формализует процесс оптимизации, позволяя автоматически настраивать параметры оценки производной таким образом, чтобы минимизировать ошибку. Это достигается путем определения функции потерь, которая количественно оценивает отклонение оцененной производной от истинного значения, и последующего использования алгоритмов оптимизации, таких как градиентный спуск, для поиска оптимальных гиперпараметров. Использование фреймворка позволяет повысить устойчивость и точность оценки производных в условиях, когда данные содержат значительный шум или выбросы, что особенно важно для алгоритмов машинного обучения и задач оптимизации.

Комбинирование предложенной структуры вычисления производных с методами, такими как RobustDiff, позволяет эффективно отбраковывать выбросы в данных и повышать точность оценки производных. Стандартные методы, такие как стохастический градиентный спуск, чувствительны к аномальным значениям, что может приводить к смещению оценок и снижению производительности модели. RobustDiff использует робастную функцию потерь, которая минимизирует влияние выбросов, придавая меньший вес наблюдениям, значительно отклоняющимся от основной тенденции. Это достигается за счет применения функции веса, основанной на остатках, что позволяет более устойчиво оценивать $\frac{\partial L}{\partial w}$ даже в условиях зашумленных или содержащих выбросы данных, где $L$ — функция потерь, а $w$ — параметры модели.

В рамках разработанной системы вычислений производных поддерживаются методы регуляризации, в частности, $L_1$-регуляризация. Применение $L_1$-регуляризации способствует повышению устойчивости получаемых решений за счет добавления штрафа за величину абсолютных значений коэффициентов модели. Это, в свою очередь, приводит к разреженности решения, то есть к обнулению некоторых коэффициентов, что упрощает модель и снижает риск переобучения, особенно при работе с данными высокой размерности. Эффективность $L_1$-регуляризации проявляется в ситуациях, когда требуется выделить наиболее значимые признаки и исключить незначительные, что повышает обобщающую способность модели и улучшает интерпретируемость результатов.

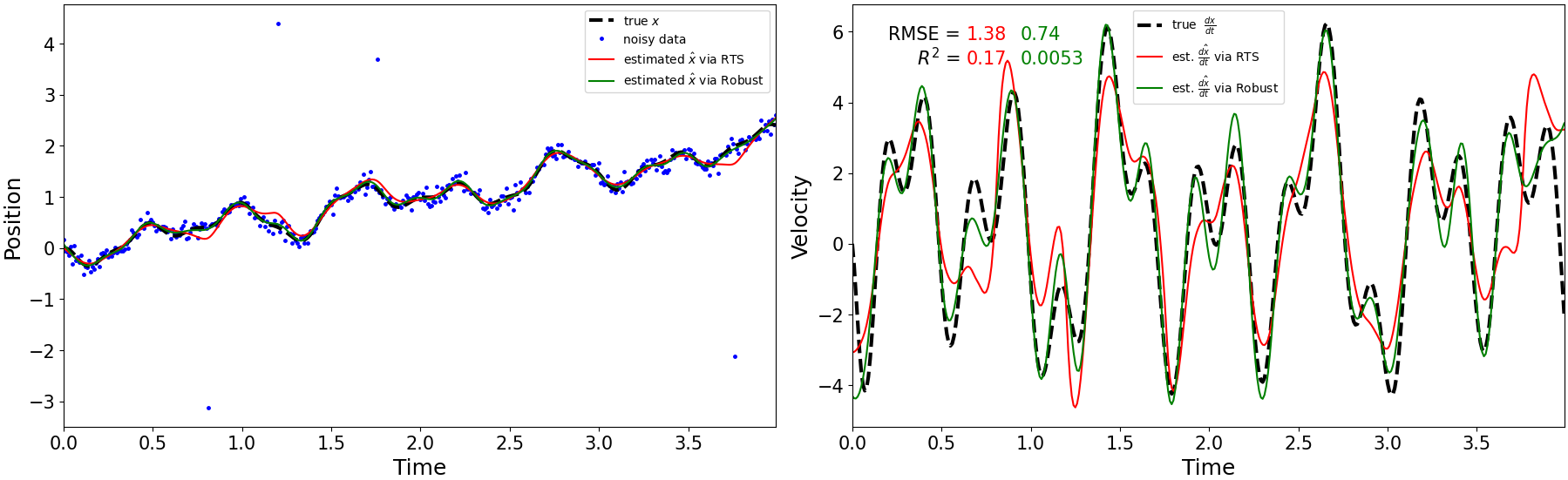
Моделирование Пространства Состояний для Повышенной Точности

Фильтр Калмана представляет собой мощную модель пространства состояний, используемую для оценки состояния системы и ее производных, основываясь на априорных знаниях. В основе работы фильтра лежит рекурсивный алгоритм, который объединяет предсказание состояния системы на основе динамической модели с измерениями, полученными от сенсоров. Априорные знания, выраженные в виде ковариационных матриц шума процесса и шума измерений, позволяют фильтру эффективно оценивать состояние даже при наличии шума и неопределенностей. Математически, фильтр Калмана решает задачу оптимальной фильтрации, минимизируя среднеквадратичную ошибку оценки состояния, и широко применяется в различных областях, включая навигацию, робототехнику и обработку сигналов. Оценка состояния и его производных осуществляется путем последовательного обновления апостериорной оценки с учетом каждого нового измерения.

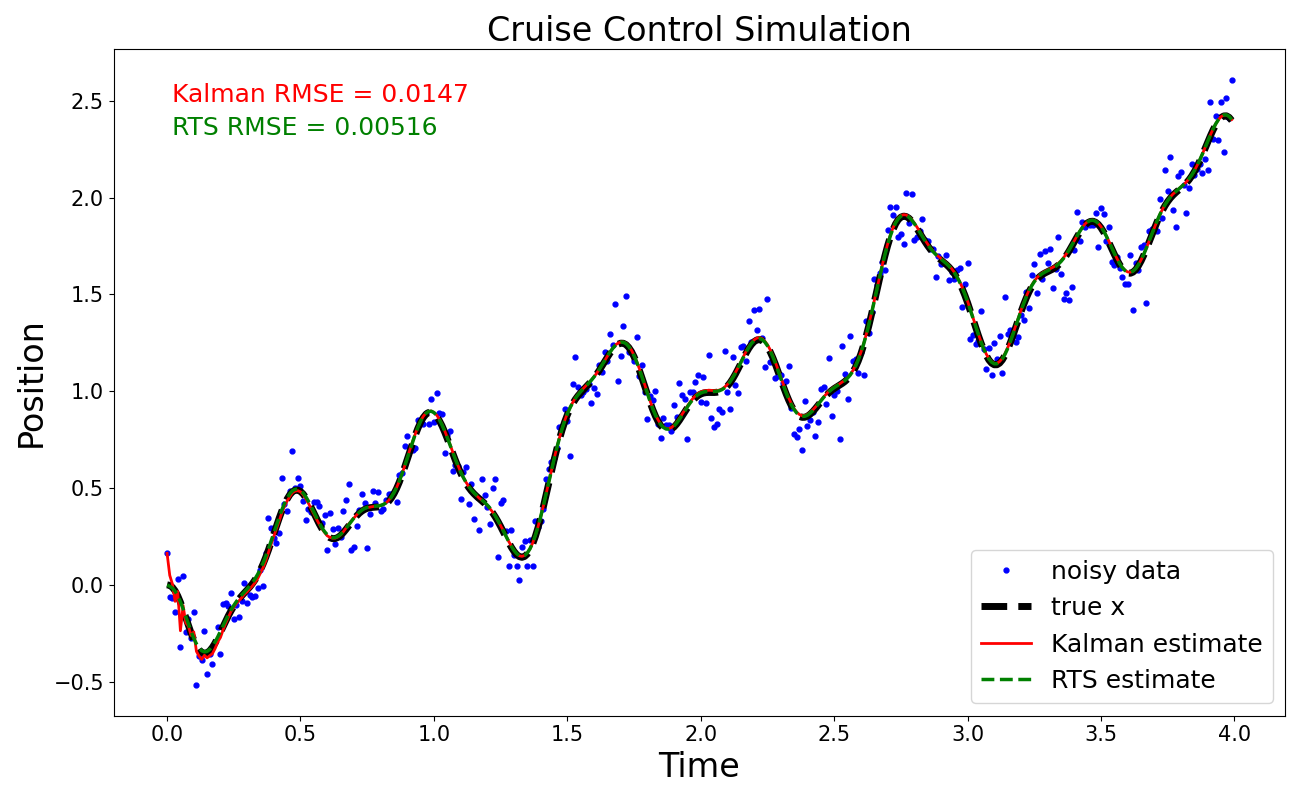
Расширение фильтра Калмана с помощью сглаживателя Рауха-Тунга-Стрибела (RTS) позволяет учитывать будущие измерения для повышения точности оценки состояния системы. В отличие от фильтра Калмана, который использует только текущие и прошлые данные, RTS использует все доступные измерения, включая будущие, для решения задачи максимальной апостериорной вероятности (MAP). Это достигается путем рекурсивного прохода в обратном направлении по временной шкале после выполнения прямого фильтра Калмана, что позволяет скорректировать оценки состояния с учетом информации, полученной из будущих измерений. Таким образом, RTS обеспечивает более точную и сглаженную оценку состояния, чем стандартный фильтр Калмана, особенно в условиях зашумленных данных или нелинейных систем.

Метод RTSDiff представляет собой подход к оценке производных, объединяющий сглаживатель Рауха-Тунга-Стрибела (RTS) с техниками дифференцирования. В результате достигается высокая точность и универсальность оценки производных состояния системы. Проведенные симуляции демонстрируют, что RTSDiff обеспечивает производительность, сопоставимую или превосходящую другие существующие методы оценки производных, включая традиционные фильтры и численные методы дифференцирования. Ключевым преимуществом является возможность использования как текущих, так и будущих измерений для повышения точности оценки $\frac{dx}{dt}$ и других производных, что особенно важно в задачах, требующих высокой точности и надежности.

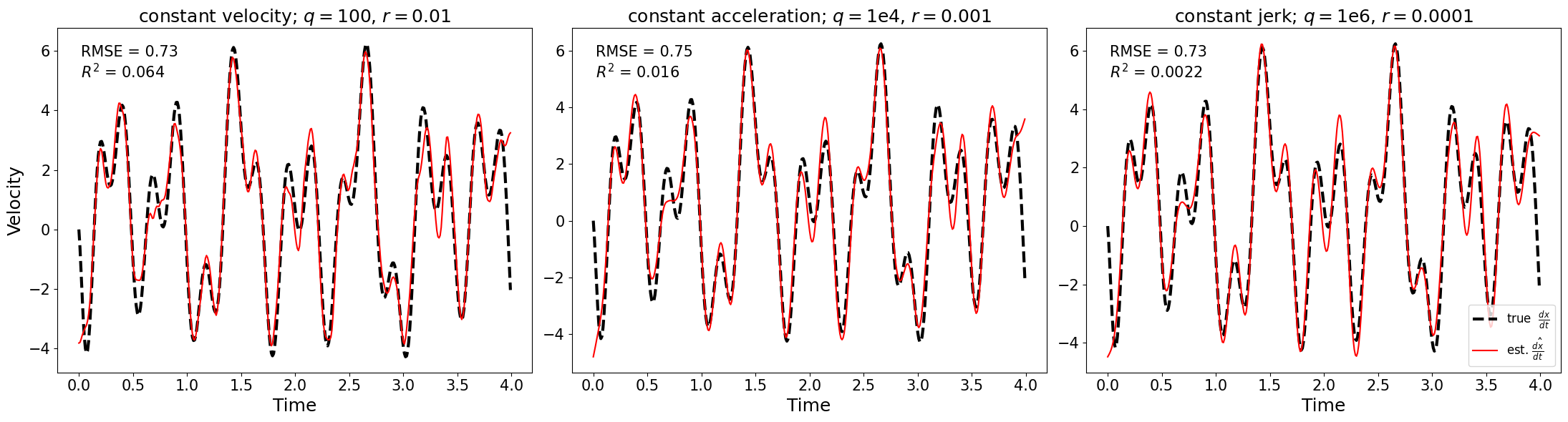
Адаптация к Сложным Данным

В случае неравномерно распределенных данных, задача обратной Вандермонда представляет собой эффективное решение для восстановления производных и аппроксимации функций. В сочетании с методами конечных разностей, она позволяет оценить производные функции, заданной в дискретных точках, без необходимости интерполяции на равномерную сетку. Этот подход особенно полезен при анализе данных, полученных в результате экспериментов или измерений, где временные интервалы между выборками могут варьироваться. Метод использует матрицу Вандермонда для представления функции в виде полинома, а затем решает обратную задачу для определения коэффициентов полинома. Полученный полином может быть продифференцирован для оценки производных в любой точке, обеспечивая высокую точность и стабильность даже при наличии шума в данных. Такое комбинированное использование позволяет эффективно обрабатывать сложные данные и извлекать из них ценную информацию о скорости изменения и других ключевых характеристиках исследуемого процесса.

В задачах, где динамические системы описываются нелинейными уравнениями, традиционный расширенный фильтр Калмана (Extended Kalman Filter, EKF) часто демонстрирует ограниченную точность из-за линеаризации нелинейных функций. Более современные варианты фильтра Калмана, такие как несмещенный фильтр Калмана (Unscented Kalman Filter, UKF), предлагают значительное улучшение. UKF использует детерминированный подход к выбору набора выборочных точек, называемых сигма-точками, которые более точно отражают распределение вероятностей нелинейной системы. Эти точки затем распространяются через нелинейную функцию состояния, что позволяет получить более точную оценку состояния и ковариации ошибки, избегая ошибок, связанных с линеаризацией, свойственных EKF. Таким образом, UKF особенно эффективен в ситуациях, когда нелинейность системы существенна, обеспечивая более надежные и точные оценки состояния.

Спектральные методы и дифференцирование в частотной области представляют собой мощный подход к оценке производных, особенно когда анализируются периодические сигналы. В отличие от традиционных методов, основанных на разностных схемах, спектральные методы используют преобразование Фурье для перехода в частотную область, где дифференцирование становится простым умножением на $i\omega$, где $\omega$ — частота. Этот подход позволяет достичь высокой точности, поскольку ошибка в оценке производной уменьшается экспоненциально с увеличением числа гармоник, используемых в разложении Фурье. В результате, спектральное дифференцирование обеспечивает значительно более гладкие и точные оценки производных по сравнению с методами, чувствительными к шуму и дискретизации, что делает его незаменимым инструментом в задачах, требующих высокой точности и стабильности, например, при анализе колебаний, волн и других периодических процессов.

Представленная работа демонстрирует, что разработанный фреймворк и методы, такие как PolyDiff и RobustDiff, обладают выраженными преимуществами в обработке сложных данных. В частности, PolyDiff позволяет проводить высокоточную аппроксимацию производных даже при использовании больших временных шагов, что существенно расширяет возможности моделирования динамических систем. В то же время, RobustDiff эффективно справляется с выбросами в данных, обеспечивая устойчивость и надежность результатов даже в условиях зашумленных или неполных измерений. Комбинация этих подходов предоставляет универсальный инструментарий для анализа разнообразных сценариев, от моделирования физических процессов до обработки сигналов и прогнозирования временных рядов, позволяя исследователям и инженерам решать широкий спектр задач с повышенной точностью и эффективностью.

Представленная работа демонстрирует необходимость целостного подхода к оценке производных, рассматривая различные методы в контексте характеристик данных и структуры задачи. Это созвучно идее о том, что система — живой организм, и изменение одной её части неизбежно влечет за собой цепную реакцию. Как отмечал Стивен Хокинг: «Главное — не просто открывать новые вещи, а понимать, как они связаны друг с другом». Данное исследование, классифицируя методы численного дифференцирования, подчеркивает важность понимания взаимосвязей между выбранным подходом, природой данных (например, наличие шума) и конечной точностью оценки производной. Оптимальный выбор метода зависит не только от математической формулы, но и от всей системы, в которой она применяется.

Куда же дальше?

Представленная классификация методов численного дифференцирования, несомненно, проливает свет на сложность оценки производных в различных условиях. Однако, элегантность любой таксономии заключается не в полноте перечисления, а в выявлении фундаментальных принципов. Очевидно, что текущие подходы часто оказываются заложниками конкретных предположений о данных — гладкости, отсутствии шума, структуре взаимосвязей. Масштабируется не вычислительная мощность, а ясность идей, и настоящим вызовом представляется разработка методов, устойчивых к неопределенности и способных адаптироваться к неожиданным особенностям данных.

Представляется важным отход от рассмотрения численного дифференцирования как изолированной задачи. Вместо этого, необходимо рассматривать его как компонент более сложной экосистемы обработки данных, где методы фильтрации Кальмана, спектральные методы и методы конечных элементов взаимодополняют друг друга. Истинный прогресс, вероятно, будет достигнут не через создание “универсального” алгоритма, а через разработку гибких фреймворков, позволяющих комбинировать различные подходы в зависимости от конкретной задачи.

В конечном счете, задача оценки производных — это лишь частный случай более общей проблемы — понимания структуры данных. Именно понимание лежащих в основе принципов, а не просто совершенствование алгоритмов, определит будущее этой области. Простота — ключ к масштабируемости, и именно к ней следует стремиться.

---

Оригинал статьи: https://arxiv.org/pdf/2512.09090.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/