Аналитика и данные
Поиск Скрытых Сигналов: Оптимизация Анализа Данных на Большом Адронном Коллайдере
Автор: Денис Аветисян
Новый подход к анализу данных, разработанный для Большого адронного коллайдера, позволяет выявлять тонкие эффекты, предсказанные теорией эффективного поля.
В работе представлена методика оптимизации наблюдаемых величин с использованием вычислений матричных элементов и машинного обучения для повышения чувствительности к новым физическим явлениям.
Несмотря на растущую точность экспериментов на Большом адронном коллайдере, выявление новых физических явлений требует оптимизации методов анализа данных. В статье ‘Maximizing Returns: Optimizing Experimental Observables at the LHC’ предложен инновационный подход, объединяющий аналитические расчеты и машинное обучение для определения оптимальных наблюдаемых, наиболее чувствительных к эффектам, предсказываемым эффективной теорией поля. Ключевым результатом является разработка нового критерия оценки (LoC) и метода снижения размерности информационного пространства, позволяющих эффективно хранить и комбинировать данные, максимизируя возможности анализа при ограниченных ресурсах. Сможет ли предложенный подход значительно ускорить поиск отклонений от Стандартной модели и открыть новую эру в физике высоких энергий?
За гранью Стандартной модели: Поиск новой физики
Несмотря на впечатляющие успехи, Стандартная модель физики элементарных частиц оставляет без ответов фундаментальные вопросы о природе Вселенной. Она не объясняет, например, природу темной материи и темной энергии, составляющих большую часть массы-энергии Вселенной, а также не дает удовлетворительного объяснения наблюдаемому преобладанию материи над антиматерией. Кроме того, модель не включает гравитацию, что указывает на необходимость более полной теории, способной объединить все известные взаимодействия. Именно эти нерешенные вопросы и стимулируют активные поиски физики за пределами Стандартной модели, направленные на обнаружение новых частиц и сил, которые могли бы расширить наше понимание фундаментальных законов природы.
Большой адронный коллайдер (БАК) играет ключевую роль в поисках физики за пределами Стандартной модели. Используя столкновения частиц на экстремальных энергиях, ученые стремятся обнаружить отклонения от предсказаний существующей теории, что может свидетельствовать о существовании новых частиц и взаимодействий. Прецизионные измерения свойств известных частиц, таких как масса и спин, а также поиск редких процессов и новых резонансов, являются основными направлениями исследований на БАКе. Эти эксперименты требуют огромной точности и анализа огромных объемов данных, что позволяет исследовать фундаментальные вопросы о природе материи и сил, управляющих Вселенной. Обнаружение даже малейшего отклонения от Стандартной модели способно радикально изменить наше понимание физики высоких энергий и открыть новую эру в науке.
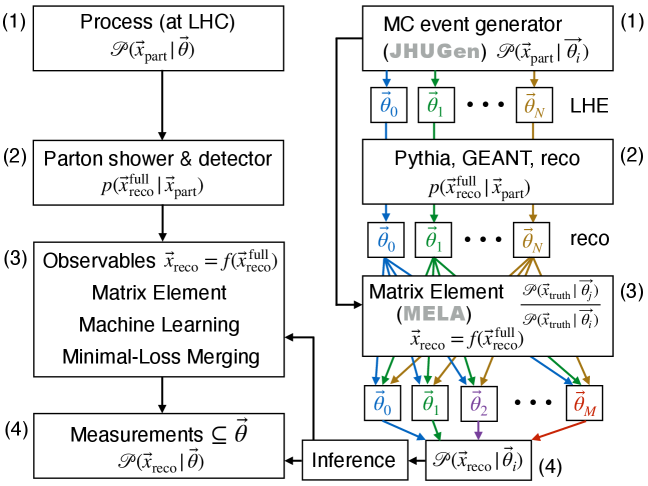
Для моделирования чрезвычайно сложных процессов, происходящих при столкновениях частиц на Большом адронном коллайдере, и проверки теоретических предсказаний, выходящих за рамки Стандартной модели, необходимы специализированные инструменты. JHUGen представляет собой мощную программную платформу, позволяющую ученым создавать и анализировать различные сценарии “новой физики”. Этот инструмент позволяет генерировать события столкновений, включающие гипотетические частицы и взаимодействия, предсказанные различными теориями, такими как суперсимметрия или дополнительные измерения. Благодаря JHUGen исследователи могут детально изучать сигнатуры этих новых явлений, сравнивать их с экспериментальными данными и, таким образом, продвигаться в понимании фундаментальных законов природы, лежащих за пределами существующей Стандартной модели. Использование подобных инструментов открывает возможности для поиска ответов на ключевые вопросы о темной материи, темной энергии и происхождении Вселенной.
Реконструкция событий на БАК: Расшифровка физики высоких энергий
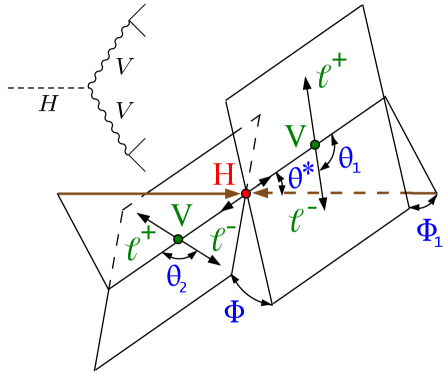
Распад бозона Хиггса на четыре лептона (H→4ℓ) представляет собой чистую сигнатуру, используемую для изучения свойств бозона Хиггса и поиска новой физики. Этот канал распада характеризуется небольшим фоновым шумом, что позволяет точно измерять параметры бозона Хиггса, такие как масса и сечение рождения. Четыре лептона, образующиеся при распаде, могут быть идентифицированы и реконструированы с высокой точностью, обеспечивая четкий сигнал, который можно отделить от других процессов, происходящих в Большом адронном коллайдере. Интенсивность сигнала H→4ℓ напрямую связана с вероятностью данного распада, что позволяет проверять предсказания Стандартной модели и искать отклонения, которые могут указывать на наличие новых частиц или взаимодействий. В частности, анализ инвариантной массы системы четырех лептонов позволяет выделить резонанс, соответствующий массе бозона Хиггса.
Точная симуляция как сигнальных, так и фоновых процессов является важнейшей частью анализа данных, получаемых на Большом адронном коллайдере. Инструменты, такие как JHUGen, позволяют генерировать события, моделируя взаимодействия частиц и их последующее распада. Это необходимо для точной оценки вероятностей различных процессов и отделения сигналов новых физических явлений от стандартного фона. Симуляция учитывает не только основные взаимодействия, но и сложные эффекты, такие как излучение фотонов и множественное производство частиц, что критически важно для сопоставления теоретических предсказаний с экспериментальными данными и получения достоверных результатов.
Вычисление вероятностей взаимодействия частиц в экспериментах на Большом адронном коллайдере (БАК) требует применения сложных методов, таких как вычисление матричных элементов (Matrix Element Calculation, MEC). MEC позволяет точно предсказывать сечения различных процессов, учитывая квантовые эффекты и характеристики частиц. Процесс включает в себя вычисление амплитуд вероятности для конкретных взаимодействий, которые затем возводятся в квадрат для получения вероятности. Точность MEC критически важна для отделения сигналов новых частиц от фонового шума и для измерения фундаментальных параметров Стандартной модели. В частности, для сложных распадов, например, распада бозона Хиггса, MEC учитывает все возможные кинематические и динамические конфигурации, что позволяет получить прецизионные теоретические предсказания, необходимые для интерпретации экспериментальных данных. \sigma = \frac{1}{\hbar} \sum_{i,f} |M_{if}|^2 \rho(i) \rho(f) , где σ — сечение, M_{if} — матричный элемент перехода между начальным состоянием i и конечным состоянием f , а ρ — плотность состояний.
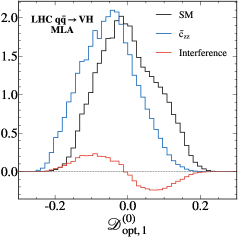
Оптимизация дискриминации: Поиск оптимальных наблюдаемых
Определение оптимального наблюдаемого является критически важным для максимизации разделения между сигналами и фоновым шумом, что напрямую влияет на чувствительность к новым физическим явлениям. Эффективное разделение позволяет более точно идентифицировать события, вызванные искомым процессом, и снизить вероятность ложных срабатываний, вызванных статистическими флуктуациями или не полностью учтенными источниками фона. Повышение разделительной способности наблюдаемого напрямую увеличивает статистическую значимость обнаружения сигнала, особенно в случаях, когда ожидается малое количество событий или сигнал слабо выражен. Таким образом, разработка и применение оптимальных наблюдаемых является ключевым аспектом в экспериментальной физике элементарных частиц и астрофизике высоких энергий.
Для оценки эффективности разработанных наблюдаемых величин, используемых в задачах разложения сигналов и фона, широко применяются ROC-кривые (Receiver Operating Characteristic) и метрика AUC (Area Under the Curve). ROC-кривая строится на основе зависимости между долей верно классифицированных сигнальных событий (True Positive Rate) и долей ложно классифицированных фоновых событий (False Positive Rate) при различных значениях отсечки для наблюдаемой величины. Площадь под этой кривой, AUC, количественно характеризует способность наблюдаемой величины разделять сигнал и фон: значение AUC, близкое к 1, указывает на отличное разделение, в то время как значение, близкое к 0.5, свидетельствует об отсутствии дискриминирующей способности. AUC = \in t_0^1 TPR(x) d FPR(x), где TPR — True Positive Rate, а FPR — False Positive Rate.
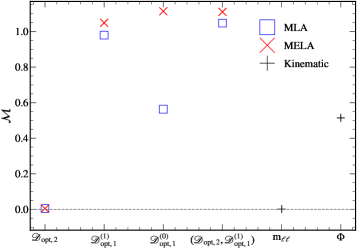
Метод MELA (Matrix Element Likelihood Approach) представляет собой аналитический фреймворк для определения оптимальных наблюдаемых величин, максимизирующих разделение между сигналами и фоном в экспериментальной физике высоких энергий. В основе метода лежит вычисление вероятности каждого события, основанной на матричных элементах диаграмм Фейнмана, соответствующих процессу сигнала и фону. Далее, события перевзвешиваются в соответствии с этими вероятностями, что позволяет усилить вклад сигнала и подавить фон, улучшая статистическую значимость наблюдаемого эффекта. Этот подход особенно полезен при анализе данных, где традиционные методы разделения оказываются недостаточными из-за перекрытия фазовых пространств сигнала и фона.
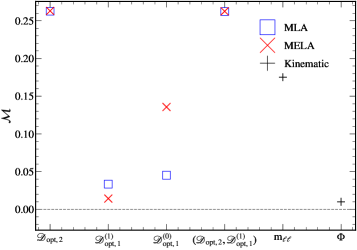
За пределами AUC: Введение метрики длины кривой
В контексте анализа эффективных теорий поля (EFT) предлагается новая метрика оценки производительности классификаторов — длина кривой (Length of the Curve, LoC). В отличие от традиционных подходов, таких как площадь под кривой (AUC), LoC ориентирована на более точную оценку в ситуациях со сложными параметрическими пространствами и нелинейными эффектами, часто встречающимися в физике высоких энергий. Данная метрика позволяет более эффективно различать модели, когда стандартные методы оказываются недостаточно чувствительными, что особенно важно при поиске новых физических явлений и ограничении параметров EFT. Применение LoC открывает возможности для более надежного анализа данных и повышения точности предсказаний в рамках EFT.
Метрика длины кривой (LoC) разработана для преодоления ограничений, присущих площади под кривой (AUC) в анализе эффективных теорий поля, особенно в случаях, когда пространство параметров становится сложным и наблюдаются нелинейные эффекты. В традиционных подходах AUC может оказаться недостаточно чувствительной к тонким различиям в классификаторах при наличии высокой размерности данных и сложных взаимосвязей между переменными. LoC, в отличие от AUC, оценивает общую «длину» кривой, разделяющей классы, что позволяет более эффективно выявлять различия между моделями даже в сложных сценариях. Такой подход особенно важен при анализе данных, полученных в экспериментах с высокой энергией, где нелинейные эффекты и сложные зависимости между параметрами являются обычным явлением, а точность классификации играет ключевую роль в интерпретации результатов.
Для реализации метрики Длины Кривой (LoC) и эффективной обработки многомерных данных, методы бинизации играют ключевую роль. В частности, усовершенствованная техника Минимального Слияния Потерь позволяет добиться почти оптимальной производительности, используя лишь 10 бинов. Это представляет собой значительное улучшение по сравнению с традиционными подходами, требующими до 22 500 бинов для достижения сопоставимых результатов. Такая высокая эффективность позволяет значительно снизить вычислительную сложность анализа, сохраняя при этом точность оценки производительности классификаторов в задачах, связанных с эффективной теорией поля. Оптимизация числа бинов является критически важной для практического применения LoC в сложных аналитических сценариях.
Теоретические основы: Связь EFT с измеримыми величинами
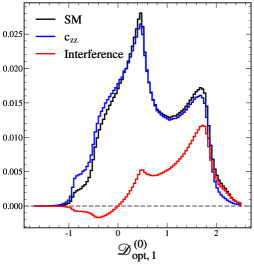
Эффективная теория поля (ЭТП) представляет собой мощный инструмент для параметризации эффектов новой физики, выходящей за рамки Стандартной модели. Вместо непосредственного построения полной теории, описывающей эти новые эффекты, ЭТП фокусируется на низкоэнергетических проявлениях, описываемых небольшим набором эффективных параметров. Эти параметры, возникающие из интеграла по степеням свободы высокоэнергетической теории, позволяют учёным систематически изучать потенциальные отклонения от предсказаний Стандартной модели. C_i коэффициенты, определяющие вклад операторов более высокой размерности, служат ключом к поиску новой физики на коллайдерах и в других экспериментах, позволяя оценить масштаб и природу этих явлений, даже без полного понимания фундаментальной теории. Такой подход позволяет исследовать широкий спектр возможных сценариев, от новых частиц до модифицированной гравитации, и является центральным элементом современных поисков за пределами Стандартной модели.
Функция переноса играет ключевую роль в связи между фундаментальными параметрами эффективной теории поля и измеримыми величинами в экспериментах на коллайдерах. Она позволяет установить соответствие между абстрактными параметрами, описывающими возможную новую физику за пределами Стандартной модели, и конкретными предсказаниями для результатов столкновений частиц. Используя функцию переноса, ученые могут рассчитывать, как изменения в этих фундаментальных параметрах повлияют на наблюдаемые характеристики, такие как сечения рассеяния или распад частиц. Это, в свою очередь, позволяет проводить точные предсказания, которые можно проверить экспериментально, и таким образом, сузить область поиска новой физики. \mathcal{T}(P) = O , где P — параметры эффективной теории, а O — наблюдаемые величины.
Для всестороннего описания возможных проявлений новой физики за пределами Стандартной модели необходимо учитывать как CP-чётные, так и CP-нечётные операторы в рамках эффективной теории поля. CP-чётные операторы влияют на величину физических эффектов, в то время как CP-нечётные операторы определяют нарушение CP-инвариантности, что может приводить к различиям в поведении частиц и античастиц. Игнорирование какого-либо из этих типов операторов приводит к неполному описанию потенциальных сигналов в экспериментах на коллайдерах. Исследование обоих типов операторов позволяет более точно моделировать взаимодействия новых частиц и выявлять тонкие эффекты, которые могут указывать на нарушение фундаментальных симметрий, что критически важно для поиска новой физики за пределами существующей модели.
Работа демонстрирует, как элегантно сформулированные теоретические построения, вроде Effective Field Theory, неизбежно сталкиваются с суровой реальностью экспериментальных данных. Авторы предлагают новый подход к оптимизации наблюдаемых, используя машинное обучение и матричные элементы, чтобы выудить слабые сигналы из шума. Но, как показывает опыт, любое “оптимальное” решение — это лишь временная передышка. Вспоминается высказывание Жан-Жака Руссо: «Человек рождается свободным, но повсюду он в цепях». Здесь “цепями” выступают ограничения детекторов, шум данных и, конечно же, неизбежные упрощения в теоретических моделях. В конечном счёте, всегда найдётся способ сломать даже самую изящную теорию, и документация по оптимизации наблюдаемых будет лишь свидетельством этого.
Что дальше?
Представленная работа, как и большинство попыток выжать максимум из экспериментальных данных, неизбежно сталкивается с границами применимости. Эффективность предложенного подхода, измеряемая кривыми ROC и метрикой LoC, напрямую зависит от адекватности используемых эффективных теорий и точности расчётов матричных элементов. Рано или поздно, новые данные заставят пересматривать даже самые элегантные модели, и оптимизированные наблюдаемые придётся оптимизировать обратно. Архитектура анализа — это не схема, а компромисс, переживший деплой.
Очевидным направлением для дальнейших исследований представляется автоматизация процесса выбора оптимальных наблюдаемых для различных сценариев выхода за рамки Стандартной Модели. Особенно актуален поиск методов, устойчивых к неполноте используемых эффективных теорий — ведь каждая «революционная» технология завтра станет техдолгом. Вопрос не в том, чтобы найти идеальную наблюдаемую, а в том, чтобы минимизировать ущерб от её неизбежной неадекватности.
Не стоит забывать и о практической стороне вопроса. Снижение вычислительной сложности, необходимое для обработки постоянно растущих объёмов данных, станет ключевым фактором успеха. В конечном счёте, мы не рефакторим код — мы реанимируем надежду на то, что хоть что-то удастся извлечь из этого хаоса частиц.
Оригинал статьи: https://arxiv.org/pdf/2601.10822.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Статья также опубликована на личном сайте автора.