Квантовые технологии
Разрушая границы: Новый подход к моделированию квантовых систем
Автор: Денис Аветисян
Исследование предлагает эффективные методы для преодоления экспоненциальных сложностей в квантовом моделировании, используя анализ светового конуса и декомпозицию на кластеры.

В статье представлены два взаимодополняющих подхода — каузальное разделение и алгебраическая декомпозиция — для эффективной симуляции квантовых систем в эпоху NISQ.
Ограниченность числа кубитов в современных квантовых компьютерах создает серьезные препятствия для моделирования сложных квантовых систем. В работе, озаглавленной ‘Estimating Local Observables via Cluster-Level Light-Cone Decomposition’, предложен новый подход, основанный на анализе светового конуса и декомпозиции кластеров, позволяющий эффективно оценивать локальные наблюдаемые. Разработанные алгоритмы — каузальное отсоединение и алгебраическая декомпозиция — позволяют снизить вычислительные затраты, связав их с глубиной схемы и связностью, а не с глобальным размером системы. Не откроет ли это путь к более глубокому исследованию локальной физики на квантовых устройствах ближайшего будущего и позволит ли преодолеть ограничения, связанные с масштабируемостью?
Пределы Современного Квантового Оборудования
Современные платформы квантовых вычислений, такие как сверхпроводящие схемы и ионные ловушки, сталкиваются с ограничениями по количеству кубитов и времени когерентности, что определяет текущую эпоху, известную как NISQ (Noisy Intermediate-Scale Quantum). Ограниченное количество кубитов препятствует решению сложных задач, требующих экспоненциального увеличения вычислительных ресурсов. При этом, время когерентности — период, в течение которого кубит сохраняет квантовую информацию — подвержено влиянию шума и декогеренции, что приводит к ошибкам в вычислениях. Эти факторы, действуя совместно, ограничивают возможности существующих квантовых компьютеров и требуют разработки новых подходов к построению и управлению квантовыми системами, чтобы преодолеть порог, необходимый для надежных и масштабируемых квантовых вычислений. Таким образом, NISQ-эра характеризуется возможностью проведения экспериментов с ограниченным количеством кубитов и необходимостью разработки алгоритмов, устойчивых к шуму.
Масштабирование монолитных квантовых архитектур сталкивается с принципиальными физическими ограничениями, препятствующими достижению отказоустойчивых вычислений. Увеличение числа кубитов в рамках единой физической системы неизбежно приводит к экспоненциальному росту сложности управления и поддержания их когерентности — способности сохранять квантовое состояние. Проблемы с перекрестными помехами, вызванными взаимодействием между кубитами, а также с поддержанием необходимой сверхнизкой температуры, становятся всё более выраженными при добавлении новых кубитов. На практике это означает, что даже при существенном увеличении числа кубитов, вероятность ошибок в вычислениях растет быстрее, чем их количество, что делает построение надежного квантового компьютера чрезвычайно сложной задачей. Таким образом, фундаментальные ограничения, связанные с физической реализацией кубитов и их взаимодействием, являются серьезным препятствием на пути к созданию квантовых компьютеров, способных решать сложные задачи, недоступные классическим машинам.
Ограничения современных квантовых аппаратных средств, связанные с количеством кубитов и временем когерентности, подталкивают к переходу от монолитных архитектур к модульным системам. Такой подход предполагает создание небольших, взаимосвязанных квантовых процессоров, которые могут быть объединены для увеличения общей вычислительной мощности. Преимущество модульного дизайна заключается в возможности обойти фундаментальные физические ограничения, связанные с производством и масштабированием единого, большого чипа. Вместо этого, усилия концентрируются на оптимизации отдельных модулей и разработке эффективных методов их взаимодействия, что открывает путь к созданию более мощных и масштабируемых квантовых компьютеров, способных решать задачи, недоступные для классических вычислительных систем. Данная стратегия представляется ключевой для преодоления текущих ограничений и достижения практической квантовой вычислительной мощности.
Строительные Блоки: Соединение Квантовых Модулей
Модульные квантовые архитектуры представляют собой перспективный подход к преодолению ограничений, связанных с масштабированием квантовых вычислительных систем. Вместо создания единого, крупномасштабного квантового процессора, предлагается построение системы из взаимосвязанных квантовых ядер (cores). Каждое ядро содержит ограниченное количество кубитов и выполняет локальные квантовые операции. Взаимодействие между ядрами осуществляется посредством классических каналов связи, что позволяет реализовать сложные квантовые алгоритмы, распределенные между несколькими модулями. Такой подход позволяет преодолеть физические ограничения, связанные с производством и управлением большим количеством кубитов в едином чипе, а также упрощает процесс разработки и отладки квантовых схем.
Для координации операций между отдельными квантовыми модулями в модульных квантовых архитектурах необходимы протоколы локальных операций и классической коммуникации (LOCC протоколы). Эти протоколы определяют, как квантовые операции выполняются локально на каждом модуле, а затем результаты передаются между модулями посредством классических каналов связи. Эффективная реализация LOCC протоколов критически важна для минимизации задержек и потерь когерентности, возникающих при обмене информацией между удаленными квантовыми ядрами. Существуют различные стратегии реализации LOCC, включая протоколы на основе телепортации, суперплотной кодировки и прямой классической коммуникации, каждая из которых имеет свои преимущества и недостатки в зависимости от топологии соединения модулей и характеристик квантовых каналов.
Наивные подходы к декомпозиции квантовых схем, такие как метод «разрезания цепи» (Circuit Cutting) и декомпозиции на основе квазивероятностей (Quasi-Probability Decompositions), приводят к значительному увеличению вычислительной сложности и проблемам масштабируемости. Метод «разрезания цепи» требует добавления дополнительных операций для передачи информации между модулями, что увеличивает глубину цепи и вероятность ошибок. Декомпозиция на основе квазивероятностей, хотя и позволяет представить квантовые операции в терминах классических вероятностей, требует экспоненциального увеличения числа классических ресурсов и операций для точного моделирования квантовых состояний, что делает её непрактичной для больших систем. Оба метода приводят к росту числа необходимых кубитов и вентилей, что существенно ограничивает их применение в архитектурах с большим количеством модулей и усложняет реализацию отказоустойчивых квантовых вычислений.
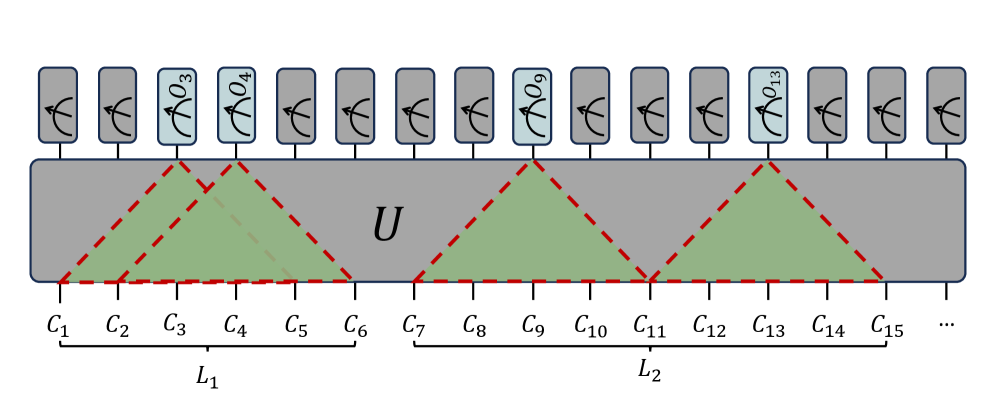
Используя Причинность: Подход Светового Конуса
Конус света, представляющий область причинно-следственного влияния, обеспечивает естественную основу для факторизации квантовых симуляций на независимые подзадачи. В рамках этой концепции, информация и влияние могут распространяться только в пределах конуса света, что позволяет определить подсистемы, которые не взаимодействуют друг с другом вне этого ограничения. Разделение общей задачи на такие независимые подзадачи существенно упрощает вычисления, поскольку позволяет выполнять симуляции параллельно и минимизировать необходимость обмена данными между различными вычислительными модулями. Этот подход особенно полезен в системах с высокой степенью связности, где традиционные методы часто сталкиваются с экспоненциальным ростом вычислительных затрат, а разделение на независимые области, ограниченные конусом света, снижает сложность задачи.
Алгоритмы, такие как Алгоритм Каузального Разделения (Causal Decoupling Algorithm) и Алгоритм Алгебраической Декомпозиции (Algebraic Decomposition Algorithm), используют концепцию светового конуса для минимизации межмодульной коммуникации в квантовых вычислениях. Оба подхода основаны на принципе, что информация может распространяться только в пределах светового конуса, определяемого скоростью света. Это позволяет декомпозировать квантовую схему на независимые модули, где каждый модуль отвечает за определенную область светового конуса. Связь между модулями ограничивается только теми событиями, которые находятся в пределах их общих световых конусов, что значительно снижает объем данных, необходимых для обмена между ними и, следовательно, уменьшает накладные расходы на коммуникацию. Минимизация межмодульной коммуникации критически важна для реализации эффективных квантовых вычислений на модульных архитектурах.
Применение концепции светового конуса на уровне кластеров позволяет эффективно декомпозировать квантовые схемы в модульных архитектурах. Данный подход обеспечивает достижение сложности выборки, равной , для полностью связанных систем. Здесь, представляет собой количество слоев в схеме, — количество кубитов на кластер, — размер кластера, — временной горизонт эволюции, — максимальная сила взаимодействия, а — требуемая точность. Сложность выборки напрямую зависит от указанных параметров, что позволяет оптимизировать ресурсы, необходимые для моделирования, в зависимости от характеристик квантовой схемы и архитектуры.
Оптимизация и Защита Модульных Схем
В рамках оптимизации и защиты модульных квантовых схем, комбинированное применение вариационных квантовых алгоритмов и алгоритма алгебраического разложения демонстрирует высокую эффективность. Такой подход позволяет разбивать сложные квантовые вычисления на более простые, модульные блоки, что существенно упрощает процесс оптимизации. Алгоритм алгебраического разложения, в частности, способствует сокращению количества необходимых квантовых операций и снижению глубины схемы. Вариационные алгоритмы, в свою очередь, позволяют находить приближенные решения задач оптимизации, адаптируя параметры схемы для достижения наилучших результатов. В результате, достигается значительное повышение производительности и масштабируемости квантовых вычислений, делая возможным решение задач, которые ранее были недоступны из-за ограничений вычислительных ресурсов и сложности схемы. Такое сочетание методов открывает новые перспективы для реализации сложных квантовых алгоритмов в практических приложениях, например, в области моделирования материалов и разработки лекарств.
Для повышения надежности модульных квантовых вычислений применяется интеграция методов квантовой коррекции ошибок с декомпозицией по световому конусу. Такой подход позволяет эффективно локализовать и исправить ошибки, возникающие в процессе вычислений, не требуя экспоненциального увеличения количества кубитов. Декомпозиция по световому конусу ограничивает распространение ошибок в пространстве-времени квантовой схемы, что в сочетании с кодами коррекции ошибок значительно снижает вероятность накопления ошибок и обеспечивает более точные результаты. Данная стратегия особенно важна для реализации сложных квантовых алгоритмов, где даже незначительные ошибки могут привести к полной неработоспособности вычислений, и позволяет добиться устойчивости вычислений даже при наличии шума и несовершенства квантового оборудования.
Предлагаемый подход к построению модульных квантовых схем демонстрирует высокую эффективность с точки зрения использования ресурсов. Достигнуто минимальное требование к количеству кубитов, равное , что существенно снижает аппаратные затраты. При этом глубина схемы масштабируется линейно относительно времени , что означает, что сложность вычислений растет предсказуемо и управляемо, даже при увеличении продолжительности процесса. Такая линейная зависимость глубины от позволяет создавать более сложные и длительные вычисления, сохраняя при этом практическую реализуемость на существующих и перспективных квантовых платформах. Данное сочетание минимальных требований к кубитам и линейной масштабируемости глубины делает предложенную архитектуру особенно привлекательной для решения широкого спектра задач, требующих ресурсоэффективных квантовых вычислений.
Будущее Масштабируемых Квантовых Вычислений
Модульные архитектуры представляют собой перспективный подход к созданию масштабируемых квантовых компьютеров, преодолевая ограничения, связанные с увеличением числа кубитов. В основе этой концепции лежит принцип декомпозиции светового конуса, позволяющий разбить сложную квантовую задачу на более мелкие, локально решаемые подзадачи. Такой подход значительно снижает требования к когерентности и точности управления отдельными кубитами, поскольку ошибки, возникающие в одном модуле, не распространяются на всю систему. Развитые методы оптимизации, включая алгоритмы минимизации ошибок и повышения связности между модулями, позволяют эффективно интегрировать эти локальные вычислительные блоки в единую, мощную квантовую систему. В результате, становится возможным создание квантовых компьютеров, способных решать задачи, недоступные для классических компьютеров, открывая новые горизонты в науке и технологиях.
В контексте модульных квантовых архитектур, стратегии, объединяющие квантовые и классические вычисления, представляются необходимыми для эффективного использования сильных сторон обеих парадигм. Квантовые процессоры, обладая потенциалом для решения определенных задач экспоненциально быстрее, чем классические компьютеры, ограничены в ресурсах и подвержены ошибкам. Классические вычисления, напротив, превосходно справляются с задачами управления, оптимизации и обработки данных. Гибридный подход позволяет распределять вычислительную нагрузку таким образом, чтобы квантовые подсистемы выполняли наиболее сложные вычисления, а классические компьютеры управляли процессом, корректировали ошибки и обрабатывали результаты. Такое взаимодействие, основанное на оптимизации распределения задач и эффективной коммуникации между квантовыми и классическими компонентами, открывает путь к созданию масштабируемых и надежных квантовых систем, способных решать практически значимые задачи в различных областях науки и техники.
Перспективы, открываемые данным подходом к квантовым вычислениям, простираются далеко за пределы существующих возможностей. Ожидается, что прорыв в материаловедении станет возможным благодаря моделированию сложных молекулярных структур и предсказанию новых материалов с заданными свойствами. В области фармацевтики это позволит ускорить процесс разработки лекарств, моделируя взаимодействие молекул и предсказывая эффективность потенциальных препаратов. Кроме того, развитие искусственного интеллекта получит мощный импульс, поскольку квантовые вычисления способны решать сложные оптимизационные задачи, недоступные классическим компьютерам, что приведет к созданию более совершенных алгоритмов машинного обучения и нейронных сетей. Подобные достижения могут кардинально изменить ландшафт науки и технологий, открывая эру, в которой сложные проблемы, ранее считавшиеся неразрешимыми, будут успешно преодолены.
Данная работа, исследуя возможности эффективной симуляции квантовых систем на модульных архитектурах, напоминает о фундаментальной сложности предсказания даже самых простых процессов. В контексте предложенного подхода, использующего анализ светового конуса для смягчения экспоненциального роста вычислительной сложности, уместно вспомнить слова Альберта Эйнштейна: «Самое непонятное — это то, что никто не понимает». Подобно тому, как авторы стремятся разложить сложную квантовую систему на более управляемые компоненты, Эйнштейн намекает на то, что даже кажущаяся простота может скрывать глубочайшую непостижимость. В конечном счёте, исследование причинно-следственной разобщенности и алгебраического разложения — это попытка не просто решить вычислительную задачу, но и прикоснуться к границам нашего понимания реальности.
Что дальше?
Представленные здесь методы декомпозиции светового конуса, как и любая попытка обуздать экспоненциальную сложность, кажутся скорее искусным откладыванием неизбежного, чем истинным решением. Иллюзия контроля над квантовой системой достигается за счёт фрагментации, но не устраняет фундаментальную проблему: каждый кусок всё равно подчиняется тем же законам, что и целое. Будущие исследования, вероятно, сосредоточатся на поиске тех редких, узкоспециализированных систем, где эта фрагментация действительно даёт значимое преимущество, а не просто перекладывает вычислительную нагрузку.
Особое внимание следует уделить границам применимости этих алгоритмов. Оптимизация для NISQ-эры — это всегда компромисс между точностью и ресурсами. Насколько чувствительны полученные результаты к шуму и ошибкам, неизбежно присутствующим в реальных квантовых устройствах? Сможем ли мы отличить истинный сигнал от артефактов, порождённых несовершенством аппаратуры? История науки полна примеров, когда элегантные математические модели разбивались о суровую реальность эксперимента.
В конечном счёте, ценность подобных исследований заключается не столько в непосредственном достижении квантового превосходства, сколько в углублении понимания фундаментальных ограничений, присущих моделированию сложных систем. Как и в случае с любым другим инструментом, важно помнить, что модель — это всего лишь упрощение, а истина всегда сложнее, чем любая её проекция.
Оригинал статьи: https://arxiv.org/pdf/2512.02377.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Статья также опубликована на личном сайте автора.