Шум Теплового Релакса: Точное Моделирование для Квантовой Защиты

---

Новый метод позволяет эффективно моделировать тепловой шум, критически важный для разработки надежных систем квантовой коррекции ошибок.

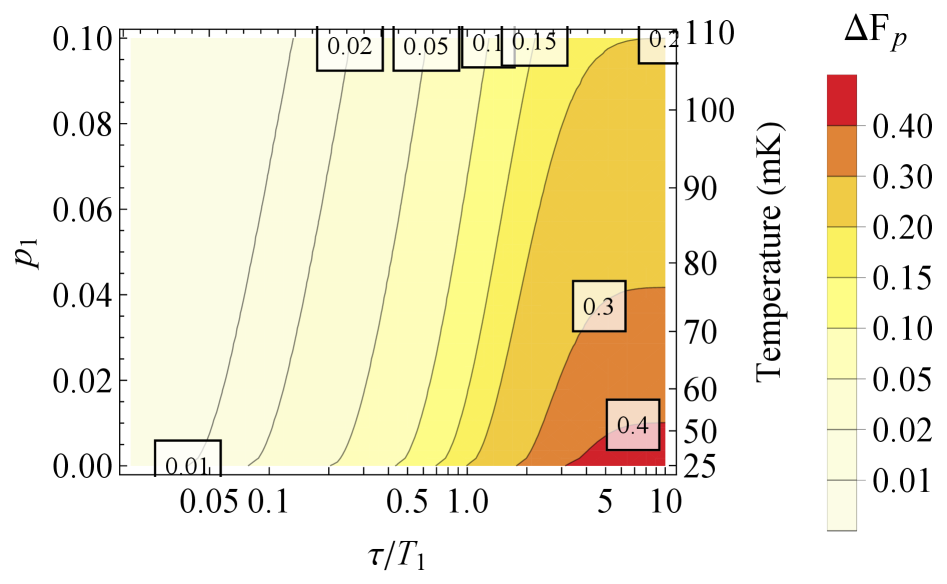
Представлен способ точного и эффективного моделирования шума теплового релакса в кодах коррекции квантовых ошибок, использующий объединенный канал амплитудного затухания и дефазировки для более масштабируемых симуляций.

Несмотря на прогресс в квантовой коррекции ошибок, точное моделирование реалистичных источников шума, таких как тепловое релаксационное возбуждение, остается сложной задачей. В работе «Exact and Efficient Stabilizer Simulation of Thermal-Relaxation Noise for Quantum Error Correction» предложен эффективный стабилизаторный метод моделирования теплового шума, объединяющий амплитудное затухание и дефазировку в единый канал. Данный подход позволяет получить точную и масштабируемую симуляцию, превосходящую по качеству приближение Паули-твирлинга, особенно при $T_2⩽T_1$. Будет ли предложенная методика способствовать разработке декодеров, более эффективно использующих структуру теплового шума в будущих отказоустойчивых архитектурах?

---

Тепловой Шум и Хрупкость Квантовых Состояний

Квантовые вычисления открывают перспективы беспрецедентной вычислительной мощности, однако кубиты, в отличие от классических битов, обладают чрезвычайной чувствительностью к внешним воздействиям. Любое взаимодействие с окружающей средой, даже незначительное, способно вызвать нежелательные изменения в квантовом состоянии кубита, приводя к потере информации и ошибкам в вычислениях. Эта уязвимость обусловлена фундаментальными принципами квантовой механики, где системы находятся в состоянии суперпозиции и подвержены декогеренции — процессу, разрушающему квантовые свойства. Для успешной реализации квантовых алгоритмов необходимо обеспечить изоляцию кубитов от шума и разработать эффективные методы коррекции ошибок, чтобы сохранить целостность квантовой информации и достичь надежных результатов вычислений. Управление этой чувствительностью является ключевой проблемой в развитии квантовых технологий.

Тепловое релаксация, процесс потери энергии квантовой системой и связанная с ним декогеренция, представляет собой серьезную угрозу для стабильности квантовой информации. В отличие от классических битов, кубиты чрезвычайно чувствительны к даже незначительным колебаниям окружающей среды, что приводит к нежелательному переходу в смешанные состояния. Этот процесс, обусловленный взаимодействием кубита с тепловыми резервуарами, быстро разрушает хрупкие квантовые состояния, необходимые для вычислений. Скорость декогеренции, зависящая от температуры и характеристик системы, определяет время, в течение которого кубит может надежно хранить и обрабатывать информацию. Поскольку время декогеренции обычно на несколько порядков меньше времени выполнения операций, поддержание когерентности является ключевой задачей при создании практических квантовых компьютеров. Эффективное подавление теплового шума и разработка методов коррекции ошибок, способных противодействовать декогеренции, являются критически важными для реализации надежных квантовых вычислений.

Построение отказоустойчивых квантовых компьютеров напрямую зависит от способности преодолеть ошибки, возникающие из-за влияния окружающей среды. Квантовые биты, будучи чрезвычайно чувствительными к возмущениям, подвержены декогеренции и потере информации, что делает надежные вычисления сложной задачей. Успешная реализация квантовых технологий требует не только разработки новых алгоритмов, но и создания эффективных методов коррекции ошибок, способных защитить хрупкое квантовое состояние от внешних воздействий. Без эффективного подавления этих ошибок, даже самые мощные квантовые алгоритмы окажутся бесполезными, а потенциал квантовых вычислений останется нереализованным. Именно поэтому исследования в области коррекции ошибок являются краеугольным камнем развития всей квантовой индустрии.

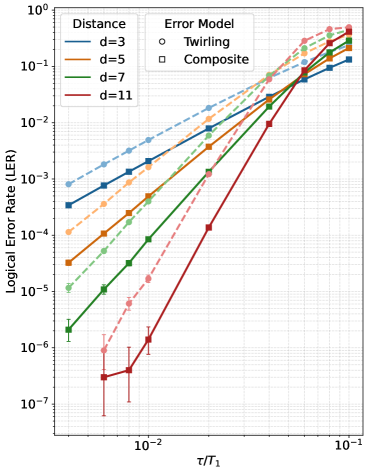
Традиционные методы коррекции ошибок в квантовых системах сталкиваются со значительными трудностями при точном моделировании теплового релакса — процесса потери энергии и декогеренции. Сложность заключается в учете множества факторов, влияющих на тепловое воздействие, что приводит к неточностям в прогнозировании и исправлении ошибок. В частности, приближения, такие как метод Паули Твирлинга, используемые для упрощения расчетов, могут приводить к занижению реальных логических ошибок в 2-10 раз. Это означает, что оценки надежности квантовых вычислений, основанные на подобных упрощениях, могут быть существенно оптимистичными, что представляет серьезную проблему для создания отказоустойчивых квантовых компьютеров и требует разработки более точных методов моделирования и коррекции ошибок, учитывающих сложность теплового релакса.

Моделирование Тепловой Релаксации: Путь к Пониманию

Для моделирования влияния внешних взаимодействий на когерентность кубитов используется детальное моделирование тепловой релаксации. Данный подход позволяет численно исследовать процессы, приводящие к декогеренции, путем учета теплового шума и других факторов окружающей среды. В процессе моделирования рассчитывается эволюция квантового состояния кубита во времени, принимая во внимание вероятности спонтанного излучения и другие механизмы релаксации, что позволяет оценить время когерентности $T_2$ и время релаксации $T_1$. Точность моделирования обеспечивается детальным учетом параметров окружающей среды и механизмов взаимодействия кубита с ней.

В рамках моделирования тепловой релаксации используется формализм стабилизаторов для эффективного отслеживания квантовых состояний при распространении ошибок. Этот подход базируется на представлении квантового состояния через стабилизаторы — операторы, коммутирующие с состоянием и определяющие его симметрии. Вместо непосредственного отслеживания волновой функции, отслеживаются только стабилизаторы, что значительно снижает вычислительную сложность, особенно для систем с большим количеством кубитов. Изменения в стабилизаторах, вызванные шумом и декогеренцией, позволяют реконструировать эволюцию квантового состояния без явного вычисления его полной волновой функции. Данный метод позволяет эффективно моделировать ошибки, сохраняя информацию о квантовой когерентности и обеспечивая точное отслеживание состояния кубитов во времени, что критически важно для оценки и улучшения характеристик квантовых вычислений.

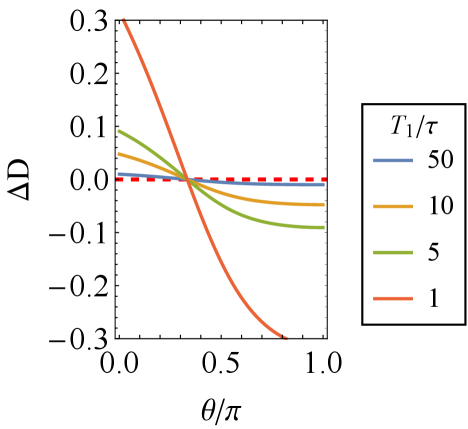
Для управления вычислительной сложностью при моделировании тепловой релаксации используются методы аппроксимации Паули и квази-вероятностного разложения. Аппроксимация Паули, посредством усреднения по случайным поворотам Паули, позволяет снизить размерность пространства состояний, сохраняя при этом важные характеристики динамики ошибок. Квази-вероятностное разложение, в свою очередь, позволяет представить операторы ошибок в виде комбинации положительно полуопределенных операторов, что необходимо для корректного моделирования эволюции квантовых состояний. Комбинация этих методов позволяет эффективно исследовать влияние тепловых взаимодействий на когерентность кубитов, минимизируя вычислительные затраты, особенно в режимах, где $T_2\le T_1$.

В разработанном нами подходе, за счет применения полностью положительного Клиффордовского разложения, удалось устранить вычислительные издержки, связанные с выборочным определением квазивероятностей, ранее возникавшие в режимах, где время дефазировки $T_2$ меньше времени релаксации $T_1$. Это позволяет эффективно моделировать динамику квантовых состояний без необходимости в сложных процедурах семплирования квазивероятностей, что существенно снижает вычислительную сложность и повышает точность симуляций в указанных режимах. Использование полностью положительного разложения гарантирует, что эволюция квантового состояния описывается физически реализуемым каналом, избегая нефизических состояний и обеспечивая достоверность полученных результатов.

Оценка Эффективности Кодов Коррекции Ошибок

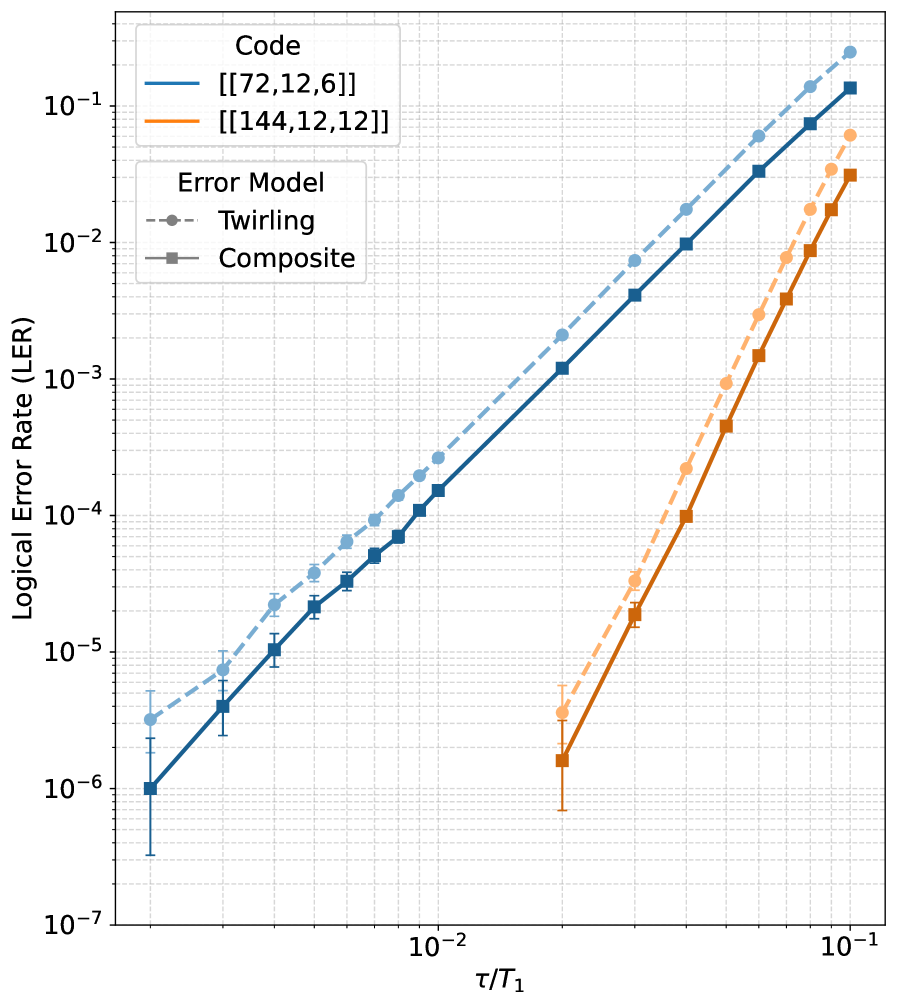
В ходе сравнительного анализа производительности кодов Surface и Bivariate Bicycle использовались реалистичные модели ошибок, обусловленных тепловой релаксацией. Данные модели учитывают вероятности возникновения ошибок, зависящие от температуры и времени, что позволяет более точно оценить эффективность коррекции ошибок в реальных условиях. В отличие от упрощенных моделей, таких как PTA-аппроксимация, использованные модели тепловой релаксации обеспечивают более детальное представление о механизмах возникновения ошибок, что критически важно для адекватной оценки возможностей кодов Surface и Bivariate Bicycle в задачах квантовой коррекции ошибок. Результаты бенчмарка демонстрируют, как каждый из кодов реагирует на специфические типы ошибок, генерируемые данными моделями.

Декодирование кодов поверхности (Surface Codes) осуществляется с использованием алгоритма минимального совершенного соответствия (Minimum Weight Perfect Matching, MWPM). Этот алгоритм рассматривает ошибки как ребра в графе, где узлы представляют собой кубиты. Задача MWPM заключается в нахождении соответствия с минимальным суммарным весом между всеми парами не связанных между собой узлов, представляющих обнаруженные ошибки. Вес каждого ребра соответствует вероятности возникновения ошибки. После нахождения оптимального соответствия, определенные кубиты объявляются ошибочными и производится коррекция, позволяющая восстановить исходные данные. Эффективность алгоритма MWPM напрямую зависит от точности оценки вероятностей ошибок и сложности графа, определяемого структурой кода поверхности.

Кодирование с использованием Bivariate Bicycle Codes (BVC) предполагает декодирование посредством алгоритма Belief Propagation (BP). В отличие от других кодов, таких как Surface Codes, использующих Minimum Weight Perfect Matching, BP позволяет достичь потенциально более высокой скорости кодирования. Это достигается за счет итеративного обмена сообщениями между узлами графа, представляющего код, что позволяет эффективно оценивать апостериорные вероятности и исправлять ошибки. Преимущество в скорости кодирования может быть критичным в задачах, требующих высокой пропускной способности, однако эффективность BP напрямую зависит от структуры кода и параметров модели шума.

Наши симуляции демонстрируют реакцию кодов Surface и Bivariate Bicycle на ошибки, генерируемые детализированными моделями тепловой релаксации. Результаты показывают, что использование этих моделей обеспечивает повышенную точность по сравнению с методами, основанными на приближении PTA (Probabilistic Threshold Approximation). В частности, более точное моделирование ошибок позволяет более эффективно оценивать и корректировать ошибки, что приводит к улучшению показателей производительности кодов и снижению вероятности сбоев в процессе декодирования. Использование детализированных моделей позволяет учесть корреляции между ошибками, которые не учитываются в приближении PTA, что особенно важно при высоких уровнях шума и сложных топологиях кодов.

Масштабирование Моделирования для Реалистичных Квантовых Систем

Моделирование теплового релакса процесса в квантовых системах, особенно при увеличении числа кубитов, требует экспоненциального роста вычислительных ресурсов. Это связано с тем, что необходимо учитывать взаимодействие множества частиц и описывать эволюцию их квантовых состояний во времени. Для достижения реалистичных результатов, симуляции должны охватывать достаточно большой объем фазового пространства, чтобы точно представлять все возможные состояния системы. В связи с этим, даже умеренное увеличение размера моделируемой системы может потребовать значительного увеличения вычислительной мощности, что становится серьезным препятствием для изучения сложных квантовых явлений и разработки эффективных методов квантовой коррекции ошибок. Достижение масштабируемых симуляций является ключевой задачей для продвижения в области квантовых вычислений.

Для моделирования тепловой релаксации в квантовых системах большого масштаба требуется значительная вычислительная мощность. В рамках данного исследования, для преодоления этих ограничений, использовано сочетание GPU-ускорения и MPI-параллелизации. Такой подход позволяет эффективно распределить вычислительную нагрузку между множеством графических процессоров и вычислительных узлов, значительно увеличивая размер моделируемых систем, состоящих из кубитов. Благодаря этому стало возможным проводить симуляции, ранее недоступные из-за вычислительных затрат, что открывает новые возможности для изучения поведения сложных квантовых систем и разработки эффективных методов квантовой коррекции ошибок. Это, в свою очередь, способствует продвижению в создании надежных и масштабируемых квантовых компьютеров.

Особое внимание в разработанных методах уделяется сохранению полной позитивности — фундаментального требования, гарантирующего физическую реалистичность моделируемых процессов. В квантовой механике, состояние системы описывается матрицей плотности, и полная позитивность этой матрицы является необходимым условием для корректного описания физической реальности. Нарушение этого условия может привести к нефизичным результатам, таким как отрицательные вероятности или нарушение принципа неопределенности Гейзенберга. Разработанные алгоритмы тщательно сконструированы таким образом, чтобы на протяжении всего процесса симуляции, даже при работе с большими системами кубитов и сложными динамическими процессами, матрица плотности оставалась полностью положительной, обеспечивая тем самым достоверность и надежность полученных результатов. Это особенно важно при моделировании релаксации и декогеренции, где неконтролируемые процессы могут быстро привести к потере квантовой информации.

Полученные в ходе моделирования данные позволяют непосредственно измерить скорость логических ошибок — ключевой показатель, определяющий жизнеспособность квантовой коррекции ошибок. В отличие от методов, основанных на Perturbative Tensor Network Approach (PTA), предложенный подход обеспечивает значительное повышение точности оценки этой скорости. Это особенно важно, поскольку PTA, хотя и вычислительно эффективен, может недооценивать истинный уровень ошибок в сложных квантовых системах, в то время как прямое измерение логической скорости ошибок, полученное в данном исследовании, дает более надежную и реалистичную картину производительности квантного оборудования. Такой подход позволяет более эффективно оценивать прогресс в разработке отказоустойчивых квантовых вычислений и оптимизировать стратегии коррекции ошибок для достижения надежных результатов, что крайне важно для практического применения квантовых технологий.

Исследование, представленное в статье, стремится к точному моделированию теплового шума — фактора, неизбежно влияющего на стабильность квантовых систем. Это стремление к симуляции реалистичных условий напоминает о границах нашего понимания. Как заметил Джон Белл: «Не существует физической теории, которая была бы настолько полна, чтобы не могла быть опровергнута экспериментально». Работа над кодами коррекции ошибок, такими как Surface Code и BB Code, является попыткой преодолеть эти ограничения, но горизонт событий, в данном случае — шум, всегда будет представлять вызов. Точность моделирования, достигнутая благодаря объединению амплитудного затухания и дефазировки в единый канал, лишь подчеркивает, насколько важна каждая деталь в борьбе за стабильность квантовой информации.

Что дальше?

Представленный метод, объединяющий амплитудное затухание и дефазировку в единый канал для моделирования теплового релаксационного шума, безусловно, является шагом вперёд в симуляции квантовой коррекции ошибок. Однако, каждый новый способ точного моделирования лишь ярче высвечивает пропасть между идеализированными моделями и хаотичной реальностью квантовых систем. Каждое новое предположение о природе шума неизбежно порождает волну публикаций, но сам космос остаётся немым свидетелем.

Следующим логичным шагом представляется не просто увеличение масштаба симуляций, а разработка методов, позволяющих учитывать корреляции в шуме, которые неизбежно возникают в реальных квантовых устройствах. В конечном итоге, научная дискуссия требует внимательного разделения модели и наблюдаемой реальности. Иначе, рискуем построить прекрасную теорию, исчезающую в горизонте событий, как и многие до неё.

Вопрос не в том, насколько точно можно смоделировать шум, а в том, возможно ли вообще полностью его учесть. Ведь сама природа квантового мира предполагает фундаментальную неопределённость. Попытки обуздать эту неопределённость, возможно, и являются источником прогресса, но и источником вечных иллюзий.

---

Оригинал статьи: https://arxiv.org/pdf/2512.09189.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/