Символьные последовательности: новый инструмент для исследования интеллекта

---

Представлен SymSeqBench — открытая платформа для генерации и анализа закономерностей в символьных последовательностях, расширяющая возможности исследований в области когнитивной науки и искусственного интеллекта.

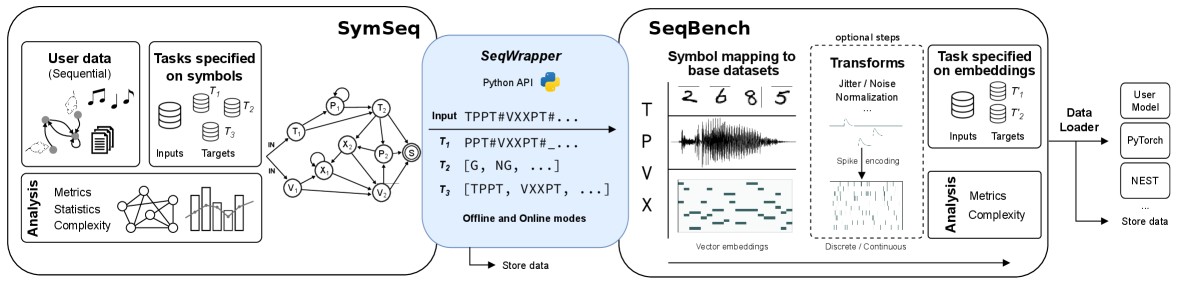
SymSeqBench — это унифицированный фреймворк для создания и оценки символьных последовательностей, основанный на правилах, позволяющий контролировать сложность и содействовать исследованиям в когнитивной науке, искусственном интеллекте и нейронауке.

Последовательности являются ключевым элементом познания и поведения, однако оценка способности к их обработке и обучению часто затруднена отсутствием унифицированных инструментов. В данной работе представлена платформа ‘SymSeqBench: a unified framework for the generation and analysis of rule-based symbolic sequences and datasets’ — комплексное решение для генерации, анализа и оценки символических последовательностей, основанное на принципах формальной теории языков. Данный фреймворк позволяет исследователям контролировать сложность последовательностей и стандартизировать эксперименты в различных областях, включая когнитивную психологию и искусственный интеллект. Сможет ли SymSeqBench способствовать разработке более эффективных моделей когнитивных процессов и систем искусственного интеллекта, способных к сложному последовательному мышлению?

---

Раскрытие закономерностей последовательностей: Основы когнитивных процессов

Многие когнитивные и поведенческие процессы по своей сути последовательны, опираются на упорядоченные цепочки символов или действий. От простых моторных навыков, таких как ходьба или письмо, до сложных процессов, как изучение языка или принятие решений, порядок элементов играет критическую роль. Например, последовательность нот определяет мелодию, а порядок слов — смысл предложения. Понимание того, как мозг обрабатывает и организует эти последовательности, имеет решающее значение для раскрытия механизмов обучения, памяти и адаптации. Именно эта зависимость от временной структуры и порядка делает многие аспекты поведения предсказуемыми, но в то же время открывает возможности для инноваций и творчества, когда привычные последовательности нарушаются или модифицируются.

Традиционные методы анализа, как правило, испытывают затруднения при работе с последовательностями, поскольку часто упускают из виду тонкие взаимосвязи и способность к порождению новых элементов, присущие этим структурам. Вместо того чтобы рассматривать последовательность как динамичную систему, где каждое звено влияет на последующие, многие подходы рассматривают ее как статичный набор дискретных единиц. Это приводит к потере информации о внутренних зависимостях и не позволяет оценить, насколько сложна и непредсказуема данная последовательность. В результате, стандартные статистические инструменты могут недооценивать истинный уровень сложности и генеративных способностей, что ограничивает их применение в моделировании когнитивных процессов и прогнозировании поведения.

Понимание структуры последовательностей имеет первостепенное значение для моделирования когнитивных процессов и прогнозирования поведения. Традиционные подходы зачастую оказываются недостаточными для анализа сложных последовательностей, упуская из виду критически важные зависимости и генеративные способности. Для адекватного описания и предсказания поведенческих паттернов необходимы надежные аналитические инструменты, способные выявлять и количественно оценивать закономерности в последовательностях действий или символов. Разработка таких инструментов позволяет не только лучше понять, как организм обрабатывает информацию, но и предсказывать его реакцию на различные стимулы, открывая новые возможности в области нейробиологии, психологии и искусственного интеллекта.

Возможность количественной оценки внутренней сложности последовательностей открывает путь к более глубокому пониманию лежащих в их основе генеративных процессов. Показатель, известный как топологическая энтропия, оказался ценным инструментом для разграничения сложности поведения у различных видов. Исследования демонстрируют существенные различия: у зебры — 20.95, у тюленя — 4.00, а у мыши — всего 3.56. Эти цифры указывают на то, что сложность поведения не является универсальной характеристикой, а зависит от видовых особенностей и, вероятно, отражает сложность нейронных сетей, управляющих этими последовательностями действий. Таким образом, количественная оценка сложности последовательностей позволяет не только описывать поведение, но и делать выводы о когнитивных способностях и адаптивности различных видов.

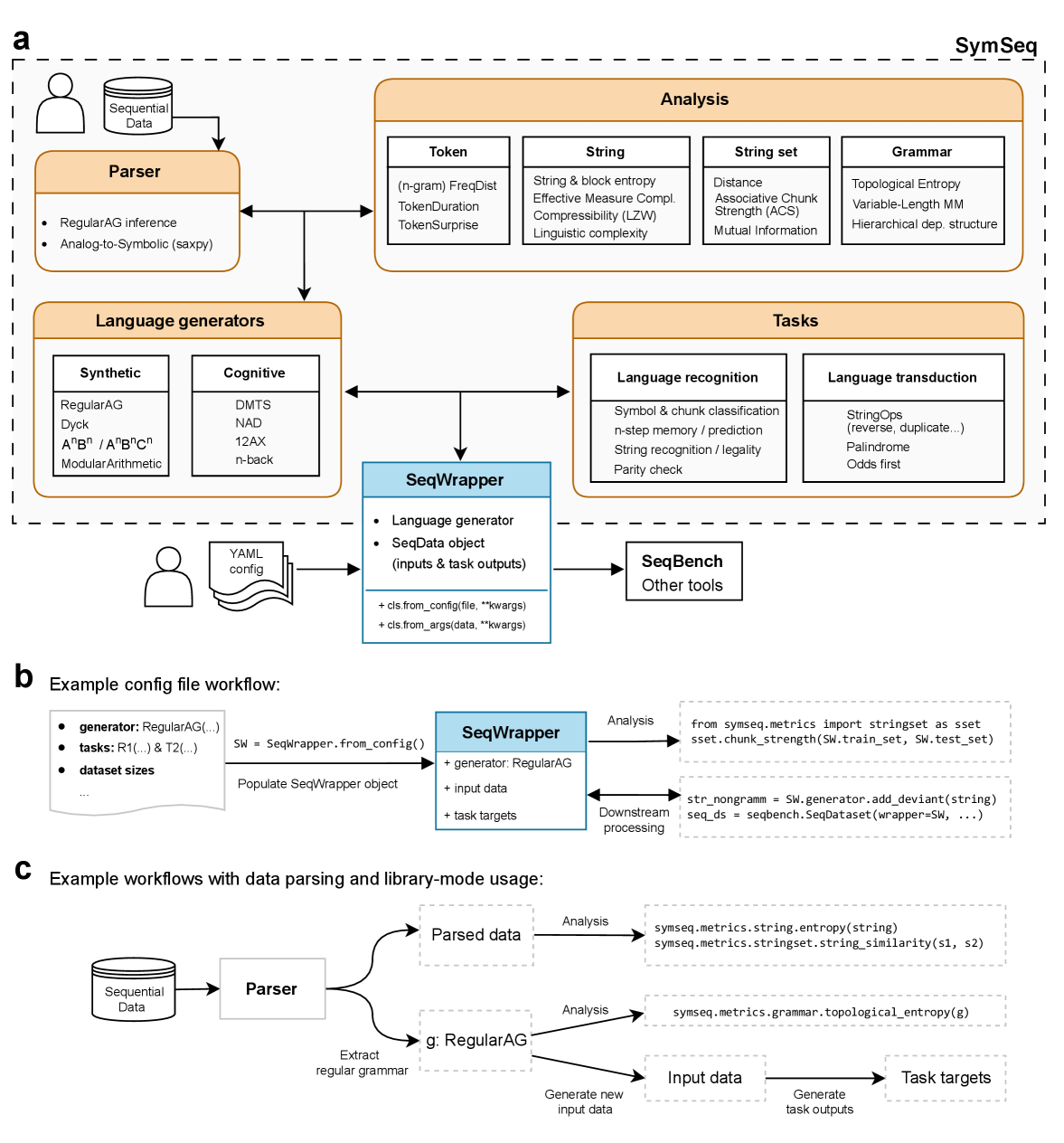
Методы анализа последовательностей: Раскрытие скрытых структур

Символический анализ последовательностей представляет собой методологию для детального изучения упорядоченных данных, направленную на выявление повторяющихся мотивов и статистических зависимостей. Данный подход предполагает разбиение последовательности на дискретные символы или элементы, после чего проводится анализ частоты встречаемости этих элементов и их взаимного расположения. Выявление рекуррентных паттернов позволяет определить внутреннюю структуру последовательности, а анализ статистических зависимостей — установить вероятностные связи между отдельными элементами. Используемые методы включают в себя построение матриц переходов, анализ корреляций и вычисление вероятностей появления определенных мотивов, что позволяет количественно оценить предсказуемость и сложность последовательности.

Оценка порядка Маркова и сложность Лемпеля-Зива предоставляют количественные показатели предсказуемости и сжимаемости последовательности, соответственно. Оценка порядка Маркова определяет, сколько предыдущих элементов последовательности необходимо учитывать для прогнозирования следующего, при этом более низкий порядок указывает на более высокую предсказуемость. Сложность Лемпеля-Зива, измеряемая количеством различных подстрок в последовательности, отражает ее сжимаемость; последовательности с меньшим количеством уникальных подстрок легче сжимаются, указывая на более высокую степень избыточности и, следовательно, предсказуемости. LZ_complexity = \frac{length(sequence)}{number\_of\_distinct\_substrings} Оба метода широко используются в анализе последовательностей для характеристики их информационной структуры и потенциала к сжатию.

Индукция грамматики направлена на выявление скрытых правил, определяющих структуру последовательности, что позволяет реконструировать ее генеративную грамматику. Этот процесс предполагает построение формальной грамматики, способной порождать наблюдаемую последовательность или ее вероятностное распределение. Алгоритмы индукции грамматики, такие как алгоритм грамматического вывода Рамона, анализируют последовательность для определения часто встречающихся подпоследовательностей и отношений между ними, создавая иерархическое описание структуры последовательности. Полученная грамматика может быть представлена в форме правил вывода, описывающих, как генерировать последовательность из базовых символов, и позволяет прогнозировать будущие элементы последовательности или идентифицировать аномалии.

Комбинированное применение методов анализа последовательностей позволяет количественно оценить содержание информации и степень сжимаемости данных с использованием метрики энтропии Шеннона H(X) = - \sum_{i=1}^{n} p(x_i) \log_2 p(x_i), где p(x_i) — вероятность появления элемента x_i в последовательности. Для оценки долгосрочных зависимостей и глубины памяти в последовательностях используется блочная энтропия, позволяющая выявить корреляции между удаленными элементами, не обнаруживаемые при анализе локальных зависимостей. Эти метрики, в совокупности с грамматической индукцией и оценкой порядка Маркова, обеспечивают комплексный подход к анализу последовательностей, выходящий за рамки простых статистических измерений.

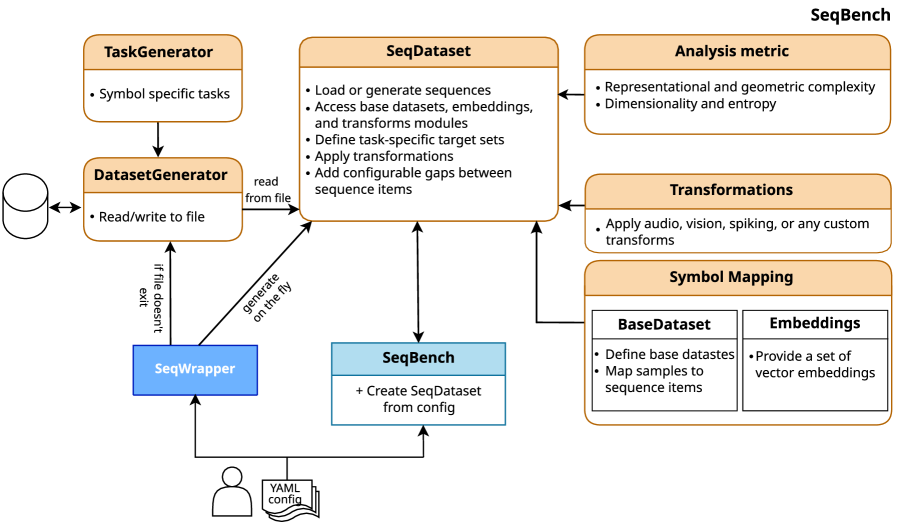
Данные и моделирование: Соединение теории и наблюдения

Последовательные наборы данных, такие как те, что получены из этограмм, документирующих поведение животных, служат эмпирической основой для последовательного анализа. Этограммы представляют собой детальные записи наблюдаемых действий животного в хронологическом порядке, позволяя создавать структурированные наборы данных, пригодные для количественного анализа. Эти данные могут включать в себя информацию о длительности каждого поведения, последовательности переходов между различными действиями и контекстуальные факторы, влияющие на поведение. Точность и полнота этих данных напрямую влияют на надежность и интерпретацию результатов последовательного анализа, включая выявление закономерностей, прогнозирование поведения и понимание адаптивных стратегий.

Нейронные сети могут быть обучены на последовательных наборах данных, таких как полученные из этограмм поведения животных, для выявления и прогнозирования закономерностей в последовательностях. Процесс обучения включает в себя представление последовательностей в числовом формате, подходящем для обработки нейронной сетью, и последующую оптимизацию параметров сети для минимизации ошибки предсказания следующего элемента в последовательности. Различные архитектуры нейронных сетей, включая рекуррентные нейронные сети (RNN) и сети долгой краткосрочной памяти (LSTM), особенно хорошо подходят для анализа последовательностей, поскольку они способны учитывать временные зависимости между элементами. Эффективность обучения напрямую зависит от размера и качества обучающих данных, а также от выбора подходящей архитектуры и параметров сети.

Эффективность моделей машинного обучения, применяемых для анализа последовательностей данных, напрямую зависит от качества и репрезентативности обучающих данных. Недостаточный объем данных, наличие шумов или систематических ошибок в данных, а также отсутствие разнообразия в представленных последовательностях могут привести к переобучению модели и снижению её способности к обобщению на новые, ранее не встречавшиеся данные. Репрезентативность подразумевает, что обучающая выборка должна адекватно отражать всю совокупность возможных последовательностей, которые модель должна уметь обрабатывать, чтобы избежать смещения результатов и обеспечить надежность прогнозов. Особенно важно учитывать факторы, влияющие на сбор данных, такие как методы наблюдения, продолжительность записи и выборка объектов наблюдения, поскольку эти факторы могут существенно влиять на статистические характеристики обучающей выборки.

Инструментарий SymSeqBench позволяет применять метрики, такие как расстояние Левенштейна (Edit Distance), для оценки сходства последовательностей, что критически важно для анализа поведенческих паттернов. Помимо этого, SymSeqBench предоставляет основу для характеризации организационных принципов в данных последовательностей посредством метрики затухания взаимной информации (Mutual Information Decay). Анализ этой метрики позволяет установить, следует ли затухание экспоненциальному или степенному закону, что дает представление о структуре и предсказуемости рассматриваемых последовательностей и лежащих в их основе процессов. MI(x;y) = \sum_{x,y} p(x,y)log\frac{p(x,y)}{p(x)p(y)}

Генеративная способность и сложность: К более глубокому пониманию

Символическая генерация последовательностей предоставляет уникальную возможность конструировать упорядоченные ряды символов, имитируя тем самым когнитивные процессы, происходящие в живых организмах, или же служа источником данных для обучения моделей машинного обучения. Этот подход позволяет создавать искусственные языки и структуры, которые затем используются для исследования принципов обработки информации в мозге, а также для разработки более эффективных алгоритмов искусственного интеллекта. В частности, путем варьирования сложности и структуры генерируемых последовательностей, можно изучать способность систем к обобщению, распознаванию закономерностей и адаптации к новым условиям, что имеет ключевое значение для понимания как биологического, так и искусственного интеллекта. Создание разнообразных последовательностей позволяет оценить производительность алгоритмов обучения и выявить их слабые места, способствуя дальнейшему развитию технологий искусственного интеллекта.

Топологическая энтропия представляет собой мощный инструмент для количественной оценки сложности формальных языков, раскрывая их потенциал в генерации разнообразных последовательностей. Этот показатель, выходящий за рамки простого подсчета символов, отражает скорость, с которой язык способен создавать новые, отличные друг от друга последовательности при увеличении их длины. Высокая топологическая энтропия указывает на язык, обладающий богатым синтаксисом и способный порождать огромное количество уникальных структур, в то время как низкая энтропия свидетельствует об ограниченном разнообразии. h = lim_{n \to \in fty} \frac{1}{n} log(L_n), где L_n — число различных последовательностей длины n, порождаемых языком. Таким образом, топологическая энтропия позволяет не только измерить сложность языка, но и предсказать его генеративные возможности, что особенно важно при анализе естественных языков и создании искусственного интеллекта.

Изучение искусственного усвоения грамматики демонстрирует удивительную способность как людей, так и машин к приобретению и интернализации правил, определяющих последовательности данных. В ходе исследований показывается, что даже при минимальном количестве примеров, системы способны выявлять скрытые закономерности и применять их для генерации новых, грамматически корректных последовательностей. Этот процесс моделирует фундаментальный аспект человеческого познания — способность к обучению на основе ограниченного опыта и экстраполяции знаний на новые ситуации. Способность к усвоению грамматики позволяет создавать алгоритмы, которые не просто распознают паттерны, но и активно строят внутреннюю репрезентацию правил, что является ключевым шагом к созданию действительно интеллектуальных систем, способных к гибкому и адаптивному поведению.

Исследования генеративных возможностей, сложности и обучения представляют собой взаимосвязанный комплекс, позволяющий глубже понять принципы функционирования как биологического, так и искусственного интеллекта. Предложенный подход, реализованный в SymSeqBench, создает целостную структуру для интерпретации этих сложных систем, рассматривая способность к генерации последовательностей, меру их разнообразия, выраженную через топологическую энтропию, и механизмы усвоения правил, как ключевые элементы. Изучение этих взаимодействий позволяет не только моделировать когнитивные процессы, но и разрабатывать более эффективные алгоритмы машинного обучения, способные к адаптации и генерации новых, нетривиальных решений. Данная методология открывает новые перспективы для анализа сложных систем, подчеркивая важность интегративного подхода к пониманию интеллекта во всех его проявлениях.

Исследование, представленное в данной работе, демонстрирует стремление к систематизации и контролю над сложностью, что находит отклик в словах Генри Дэвида Торо: «В дикой природе нет ничего обычного». SymSeqBench, как унифицированная платформа для генерации и анализа символических последовательностей, позволяет исследовать закономерности, лежащие в основе сложных систем, подобно тому, как естествоиспытатель изучает мир природы. Способность контролировать сложность последовательностей, предложенная авторами, открывает новые возможности для изучения когнитивных процессов и нейронных сетей, а также для разработки более эффективных алгоритмов машинного обучения. Этот подход, основанный на формальной теории языков и вычислительной сложности, позволяет создавать и анализировать последовательности с заданными свойствами, что является ключевым для понимания принципов обучения и адаптации в сложных системах.

Что дальше?

Представленный фреймворк, SymSeqBench, открывает возможности для систематического изучения символических последовательностей, однако истинное понимание закономерностей требует не только генерации, но и критической оценки границ применимости формальных моделей. Следующим этапом представляется разработка метрик, способных улавливать нюансы сложности, выходящие за рамки классической теории вычислительной сложности — ведь элегантность грамматики не всегда коррелирует с когнитивной правдоподобностью.

Особенно актуальным представляется исследование взаимодействия между символическими последовательностями и нейроморфными вычислениями. Возможность реализации генеративных грамматик на специализированном оборудовании может пролить свет на принципы, лежащие в основе когнитивных процессов, но лишь при условии, что мы не поддадимся искушению упрощать реальность до математической абстракции. Визуальная интерпретация, как известно, требует терпения: быстрые выводы могут скрывать структурные ошибки.

В конечном счете, ценность SymSeqBench заключается не в создании идеального инструмента, а в постановке вопросов, требующих дальнейших исследований. Понимание системы — это исследование её закономерностей, и только время покажет, насколько глубоко мы сможем проникнуть в мир символических последовательностей, не потеряв при этом связь с реальностью.

---

Оригинал статьи: https://arxiv.org/pdf/2512.24977.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/