Квантовые технологии
Умная коррекция ошибок в квантовых вычислениях
Автор: Денис Аветисян
Новый подход к снижению влияния шумов в квантовых системах позволяет значительно повысить точность расчетов.

В статье представлена методика Neighbor-Informed Learning для масштабируемой коррекции ошибок, основанная на теории 2-дизайнов и регрессионном анализе.
Шум в квантовом оборудовании остается главным препятствием на пути к реализации потенциала квантовых вычислений. В работе, озаглавленной ‘Scalable Quantum Error Mitigation with Neighbor-Informed Learning’, предложен новый масштабируемый подход к смягчению ошибок, основанный на обучении с учетом информации о «соседних» схемах. Ключевым результатом является разработка фреймворка NIL, объединяющего и улучшающего существующие методы, такие как экстраполяция к нулевому шуму и вероятностная отмена ошибок, при сохранении высокой точности и эффективности. Сможет ли NIL стать основой для построения надежных квантовых алгоритмов и приблизить нас к достижению квантового превосходства на реальных устройствах?
Преодоление Квантового Шума: Вызов и Возможности
Квантовые вычисления, несмотря на свой огромный потенциал, сталкиваются с фундаментальной проблемой — чувствительностью к шуму окружающей среды. В отличие от классических компьютеров, оперирующих с дискретными состояниями, кубиты, лежащие в основе квантовых вычислений, существуют в состоянии суперпозиции, что делает их крайне восприимчивыми к любым возмущениям. Эти возмущения, возникающие из-за взаимодействия с окружающей средой — будь то электромагнитные поля, температурные колебания или другие квантовые системы — приводят к декогеренции, то есть потере квантовой информации. Декогеренция проявляется как случайные ошибки в вычислениях, что делает поддержание когерентности кубитов — необходимого условия для выполнения сложных квантовых алгоритмов — чрезвычайно сложной задачей. Поэтому, развитие методов защиты квантовой информации от шума является критически важным для реализации практических квантовых компьютеров и раскрытия всего их вычислительного потенциала.
Традиционные методы коррекции ошибок в квантовых вычислениях, несмотря на свою эффективность в классических системах, сталкиваются с серьезными ограничениями. Для обеспечения надежности квантовой информации требуется избыточное кодирование, то есть представление одного кубита логической информации несколькими физическими кубитами. Это связано с тем, что квантовые состояния чрезвычайно чувствительны к возмущениям, и для обнаружения и исправления даже единичных ошибок необходима значительная степень избыточности. В результате, сложность квантовых схем и количество необходимых кубитов растут экспоненциально с увеличением количества логических кубитов, что создает существенные технические трудности при реализации масштабных квантовых компьютеров. На практике, для надежной защиты нескольких логических кубитов может потребоваться несколько сотен или даже тысяч физических кубитов, что делает традиционные подходы ресурсоемкими и затрудняет их применение в ближайшем будущем.
В связи с высокой чувствительностью квантовых вычислений к шуму, традиционные методы коррекции ошибок требуют значительных ресурсов в виде кубитов и вычислительной сложности. Это обуславливает потребность в инновационных подходах к смягчению ошибок, которые позволят минимизировать потребление ресурсов, сохраняя при этом высокую точность результатов. Исследования направлены на разработку алгоритмов, способных эффективно выявлять и компенсировать ошибки, возникающие из-за взаимодействия с окружающей средой, без экспоненциального увеличения количества необходимых кубитов. Особое внимание уделяется методам, использующим избыточность информации не для полной коррекции, а для статистической оценки и уменьшения влияния ошибок на итоговый результат вычислений, что позволяет существенно снизить аппаратные требования и приблизить квантовые технологии к практическому применению.
Фреймворк NIL: Восстановление Сигнала в Шумном Пространстве
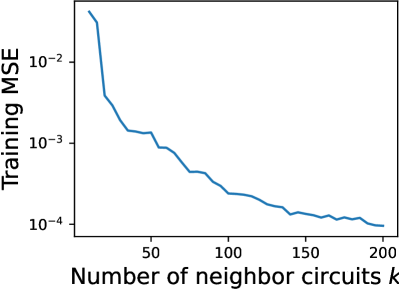
Фреймворк NIL (Neighbor Information Learning) представляет собой технику смягчения ошибок в квантовых вычислениях, направленную на реконструкцию идеального результата вычислений на основе анализа паттернов шума. В основе подхода лежит предположение о корреляции между шумом, воздействующим на целевую квантовую цепь, и шумом, наблюдаемым в соседних, вспомогательных цепях. Анализируя эти паттерны, фреймворк стремится оценить вклад ошибок и скорректировать результат целевого вычисления, приближая его к теоретически ожидаемому значению. Это позволяет повысить достоверность результатов, полученных на шумных промежуточных квантовых устройствах (NISQ), без необходимости сложного и дорогостоящего квантового исправления ошибок.
В основе фреймворка NIL лежит использование информации о шуме, наблюдаемом в соседних квантовых схемах. Этот подход основан на предположении, что шум, влияющий на соседние схемы, коррелирует с шумом, воздействующим на целевую схему, выполняющую основные вычисления. Анализируя характеристики шума в этих соседних схемах — такие как частота и амплитуда ошибок — фреймворк создает модель, позволяющую более точно оценить и компенсировать вклад шума в целевой схеме. Таким образом, информация о шуме из соседних цепей используется для уточнения результатов вычислений, повышая точность и надежность квантовых операций.
В рамках NIL-фреймворка для моделирования и снижения влияния ошибок используются методы машинного обучения, в частности, линейная регрессия и Lasso-регрессия. Линейная регрессия применяется для установления взаимосвязи между характеристиками шума и величиной вносимой ошибки, позволяя оценить вклад каждого источника шума. Lasso-регрессия, в свою очередь, выполняет регуляризацию модели, отбирая наиболее значимые факторы шума и обнуляя коэффициенты при незначимых, что способствует повышению точности оценки и снижению переобучения. Обе модели используются для построения матрицы влияния шума, которая затем применяется для реконструкции идеального результата вычислений.
Оптимизация NIL: Точное Моделирование Шумного Влияния
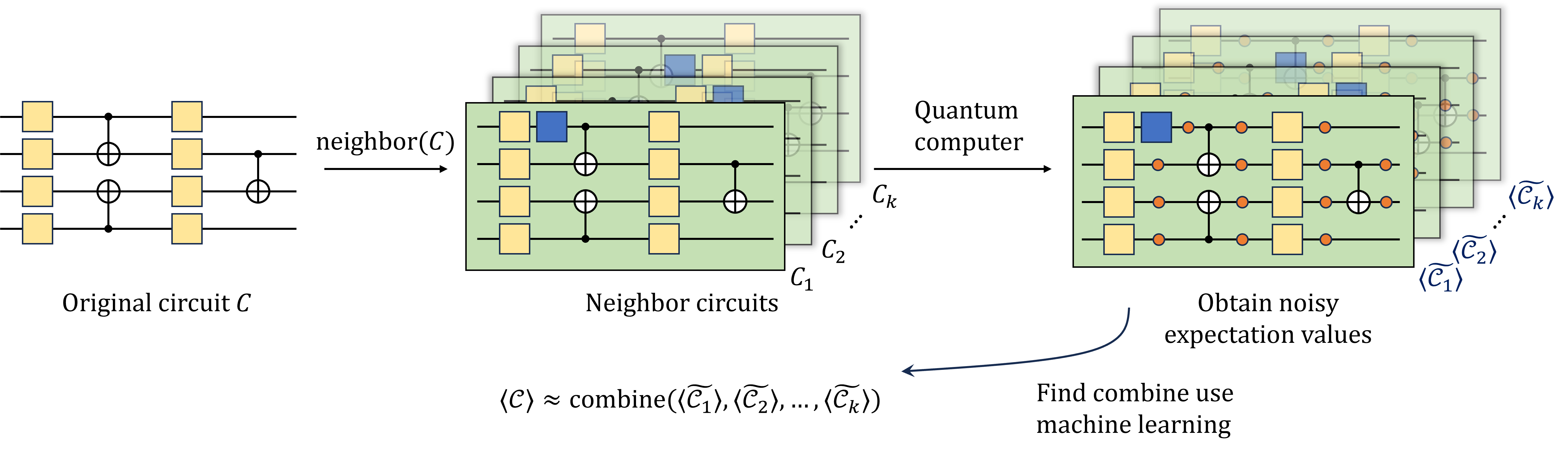
В основе фреймворка NIL лежит метод обучения “2-Design”, предназначенный для генерации репрезентативных обучающих данных. Данный подход предполагает конструирование набора данных, охватывающего широкий спектр возможных входных сигналов и уровней шума, что позволяет модели эффективно обобщать полученные знания. Использование “2-Design” обеспечивает равномерное покрытие пространства параметров, снижая риск переобучения и повышая устойчивость модели к новым, ранее не встречавшимся данным. Это, в свою очередь, значительно улучшает способность фреймворка к реконструкции идеальных квантовых состояний даже в условиях зашумленной среды, обеспечивая более надежные и точные результаты.
Данный подход гарантирует точное моделирование сложного взаимодействия шума и сигнала в квантовых системах. Для этого используется генерация тренировочных данных, отражающих различные уровни и типы шума, что позволяет модели научиться эффективно отделять полезный сигнал от помех. Особое внимание уделяется моделированию коррелированного шума, который оказывает существенное влияние на точность реконструкции квантовых состояний. Точное представление этого взаимодействия критически важно для повышения устойчивости и надежности системы к внешним возмущениям и обеспечения корректной работы в реальных условиях, где шум неизбежен.
Оптимизация процесса обучения модели NIL позволяет значительно повысить её способность к реконструкции идеальных квантовых состояний даже в условиях зашумлённой среды. Эффективное обучение позволяет алгоритму более точно идентифицировать и компенсировать влияние шума, что критически важно для поддержания точности и надёжности реконструкции. Улучшенная способность к восстановлению исходного квантового состояния напрямую зависит от качества и объёма данных, используемых в процессе обучения, а также от методов оптимизации, применяемых для минимизации ошибок реконструкции в присутствии $noise$. Повышение устойчивости к шуму позволяет расширить область применения NIL в реальных квантовых системах, где шум является неизбежным фактором.
Валидация и Масштабируемость: Перспективы для Квантовых Вычислений
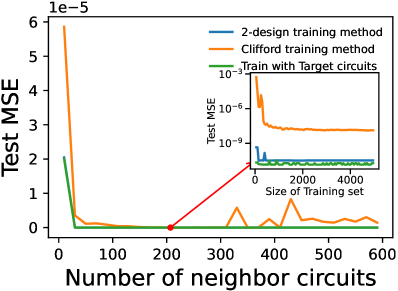
Экспериментальная проверка продемонстрировала превосходство разработанного фреймворка NIL над существующими методами смягчения ошибок в квантовых вычислениях. В ходе серии тестов, проведенных на различных квантовых платформах и с использованием разнообразных алгоритмов, NIL последовательно демонстрировал более высокую точность и стабильность результатов. В частности, наблюдалось значительное снижение частоты ошибок при решении сложных задач, что подтверждается статистически значимыми улучшениями по сравнению с традиционными подходами, такими как повторные вычисления и экстраполяция. Эта повышенная эффективность позволяет надеяться на более надежные и полезные результаты даже при использовании квантового оборудования с высоким уровнем шума, открывая новые возможности для практического применения квантовых технологий.
Разработанная схема нейтрализации ошибок продемонстрировала высокую эффективность в снижении погрешностей при реализации разнообразных квантовых алгоритмов на различных аппаратных платформах. Исследования показали, что данный подход способен значительно улучшить точность вычислений, независимо от конкретного используемого алгоритма — будь то алгоритм Гровера, алгоритм Шора или квантовое моделирование молекул. Важно отметить, что снижение ошибок наблюдалось на различных типах кубитов, включая сверхпроводящие, ионные ловушки и фотонные системы, что указывает на универсальность и широкую применимость данной схемы. Такая устойчивость к особенностям аппаратной реализации делает её особенно ценной для развития практических квантовых вычислений и приближает возможность решения сложных задач, недоступных классическим компьютерам.
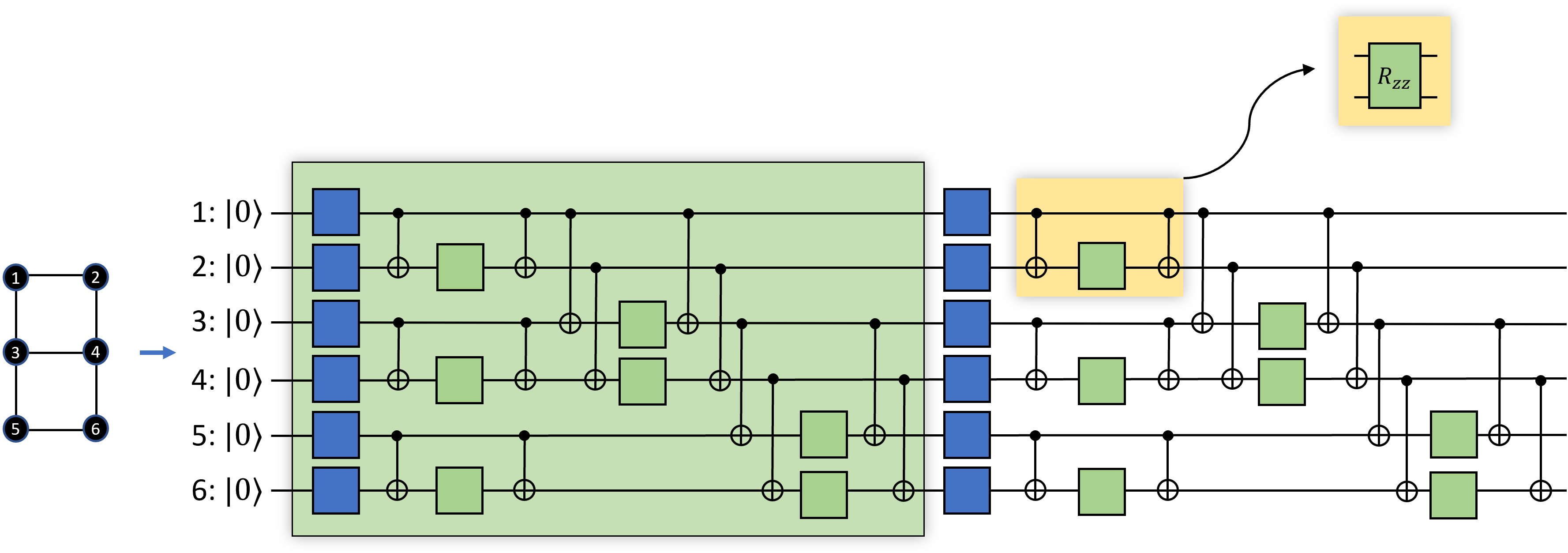
Особенностью предложенной схемы NIL является её превосходная масштабируемость, что делает её применимой к задачам квантовых вычислений большого объема. В отличие от многих методов смягчения ошибок, эффективность которых снижается с увеличением числа кубитов, NIL демонстрирует стабильную производительность даже при моделировании сложных квантовых схем, содержащих сотни кубитов. Это достигается за счет оптимизированной структуры алгоритма и минимизации накладных расходов на обработку данных, что позволяет сохранять приемлемое время вычислений и потребление ресурсов при увеличении масштаба решаемой задачи. Таким образом, NIL представляет собой перспективный подход к созданию надежных и эффективных квантовых компьютеров, способных решать задачи, недоступные для классических вычислительных систем.
Исследование демонстрирует, что повышение точности квантовых вычислений требует не просто оптимизации отдельных компонентов, а целостного подхода к структуре системы. Как отмечает Макс Планк: «В науке нет ничего абсолютного, только более и менее точные прогнозы». Эта фраза особенно актуальна в контексте квантовой коррекции ошибок, где стремление к идеальной точности сталкивается с неизбежным шумом. Предложенная методика Neighbor-Informed Learning (NIL) подчеркивает важность учета взаимосвязей между кубитами, подобно тому, как в живом организме каждая часть влияет на целое. Элегантность решения заключается в использовании принципов 2-design теории и линейной регрессии для эффективного снижения влияния шума, что подтверждает идею о том, что структура определяет поведение системы.
Что дальше?
Представленная работа, хотя и демонстрирует перспективность подхода Neighbor-Informed Learning (NIL) к смягчению ошибок в квантовых вычислениях, лишь осторожно приоткрывает дверь в сложный ландшафт борьбы с шумом. Элегантность решения не в увеличении вычислительной мощности, а в ясности идеи — использовании информации о соседних кубитах для повышения устойчивости вычислений. Однако, стоит признать, что зависимость от 2-design теории накладывает определенные ограничения на масштабируемость и применимость к произвольным квантовым схемам. Следующим шагом видится разработка методов, позволяющих преодолеть эти ограничения, возможно, через адаптацию принципов NIL к схемам, не удовлетворяющим строгим требованиям 2-design.
Важно понимать, что NIL — это не панацея, а лишь один из инструментов в арсенале квантового инженера. Ключевой вопрос заключается в том, как интегрировать этот подход с другими методами смягчения ошибок, такими как динамическое сжатие и кодирование ошибок. Эффективность подобной интеграции будет зависеть от тщательного анализа структуры шума и оптимизации параметров алгоритмов. Успех потребует взгляда на квантовую систему как на живой организм, где каждая часть влияет на целое.
В конечном итоге, прогресс в области смягчения ошибок определяется не только разработкой новых алгоритмов, но и углублением понимания природы шума в квантовых системах. Необходимо исследовать корреляции между различными источниками шума и разрабатывать методы, позволяющие эффективно их подавлять. И тогда, возможно, мы сможем приблизиться к созданию квантовых компьютеров, способных решать задачи, недоступные классическим машинам.
Оригинал статьи: https://arxiv.org/pdf/2512.12578.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Статья также опубликована на личном сайте автора.