Квантовые технологии
Ускорение квантохимических расчётов: новый подход к плотностной аппроксимации
Автор: Денис Аветисян
Исследователи разработали адаптивный алгоритм, использующий 8-битные целочисленные вычисления на AI-ускорителях для значительного повышения скорости вычислений плотностной аппроксимации.
Адаптивное смешанное машинное обучение с использованием INT8 GEMM на Tensor Cores для ускорения вычислений плотностной аппроксимации в квантохимии.
Несмотря на стремительное развитие вычислительной мощности, задачи квантохимических расчетов, требующие высокой точности, остаются ресурсоемкими. В данной работе, посвященной ‘Accelerating Density Fitting with Adaptive-precision and 8-bit Integer on AI Accelerators’, предложен адаптивный алгоритм, использующий целочисленную арифметику INT8 и тензорные ядра для ускорения метода плотностной подгонки. Показано, что разработанный подход позволяет добиться значительного прироста производительности — до 364% на графических ускорителях NVIDIA RTX — без потери точности вычислений энергии. Возможно ли дальнейшее расширение применения специализированного аппаратного обеспечения для решения сложных задач современной квантовой химии?
Вычислительные Пределы Квантовой Химии
Вычислительная химия, являющаяся краеугольным камнем материаловедения и разработки лекарственных препаратов, сталкивается с фундаментальным ограничением, обусловленным высокой стоимостью вычисления интегралов электронного отталкивания. Эти интегралы, описывающие взаимодействие между электронами в молекуле, требуют огромных вычислительных ресурсов, особенно при моделировании сложных систем. Увеличение точности расчетов, необходимое для предсказания свойств материалов и эффективности лекарств, напрямую связано с экспоненциальным ростом вычислительной нагрузки, что делает моделирование крупных молекул и сложных химических процессов чрезвычайно трудоемким. По сути, этот вычислительный барьер ограничивает возможности точного моделирования и предсказания поведения молекул, замедляя прогресс в разработке новых материалов и лекарственных средств.
Традиционные методы квантово-химических расчетов, несмотря на свою высокую точность, сталкиваются с серьезными ограничениями при моделировании сложных молекулярных систем. Проблема заключается в том, что вычислительные затраты этих методов растут экспоненциально с увеличением числа атомов в рассматриваемой молекуле. Например, для расчета энергии взаимодействия электронов в молекуле необходимо учитывать все возможные комбинации электронных пар, что приводит к N^4 зависимости времени вычислений от числа базисных функций N. Это означает, что удвоение размера молекулы увеличивает время расчетов в шестнадцать раз, делая моделирование крупных биомолекул или материалов практически невозможным с использованием стандартных вычислительных ресурсов. В результате, исследователи постоянно ищут новые алгоритмы и подходы, позволяющие снизить вычислительную сложность и расширить границы моделируемых систем.
В основе вычислительных трудностей квантохимических расчетов лежит колоссальная потребность в ресурсах для выполнения операций GEMM (General Matrix Multiplication) с использованием чисел формата FP64 (double-precision floating-point). Именно эти операции, связанные с построением и манипулированием интегралами электронного взаимодействия, являются наиболее затратными. Сложность заключается в том, что количество вычислений для GEMM растет кубически с увеличением размера матрицы, что делает моделирование больших молекулярных систем крайне проблематичным. O(N^3) — эта асимптотическая сложность обуславливает экспоненциальный рост времени расчета при увеличении числа базисных функций, используемых для описания электронной структуры. Разработка новых алгоритмов и аппаратных решений, направленных на оптимизацию операций GEMM, представляется ключевым направлением в преодолении этого вычислительного барьера и расширении возможностей квантохимического моделирования.
Плотное Приближение: Первый Шаг к Эффективности
Метод плотностной аппроксимации (Density Fitting) позволяет значительно ускорить вычисления за счет приближения двухелектронных интегралов с использованием вспомогательных базисных функций. Традиционные вычисления двухелектронных интегралов имеют сложность N^4, где N — число базисных функций. Применение плотностной аппроксимации снижает эту сложность до N^3 за счет замены исходных интегралов суммой по вспомогательным функциям. Вспомогательные базисные функции выбираются таким образом, чтобы минимизировать ошибку приближения, обеспечивая приемлемую точность при значительном снижении вычислительных затрат, особенно при работе с большими молекулярными системами и расширенными базисными наборами.
Вычисление кулоновской и обменно-корреляционной матриц является ключевым этапом в методе плотностного приближения. Эффективность этого метода напрямую зависит от скорости выполнения операций матричного умножения, поскольку обе матрицы формируются посредством перемножения матриц, представляющих вспомогательные базисные функции. Сложность этих операций масштабируется как O(N^3), где N — размер матриц, что делает оптимизацию матричного умножения критически важной для повышения производительности, особенно при работе с большими системами и расширенными базисными наборами, такими как Gaussian Basis и def2-TZVPP Basis Set.
Несмотря на эффективность методов уплотнения плотности (Density Fitting), ускорение базовых операций перемножения матриц FP64 (FP64 GEMM) остаётся важным для повышения производительности при работе с большими системами и базисными наборами, такими как Gaussian Basis и def2-TZVPP Basis Set. Увеличение размера базисного набора и количества электронов в системе приводит к экспоненциальному росту размерности матриц, участвующих в вычислениях. В результате, даже небольшое ускорение операций FP64 GEMM может существенно сократить общее время вычислений, особенно при расчётах, требующих высокой точности и масштабируемости.
Смешанная Точность и INT8 GEMM: Ускорение Вычислений
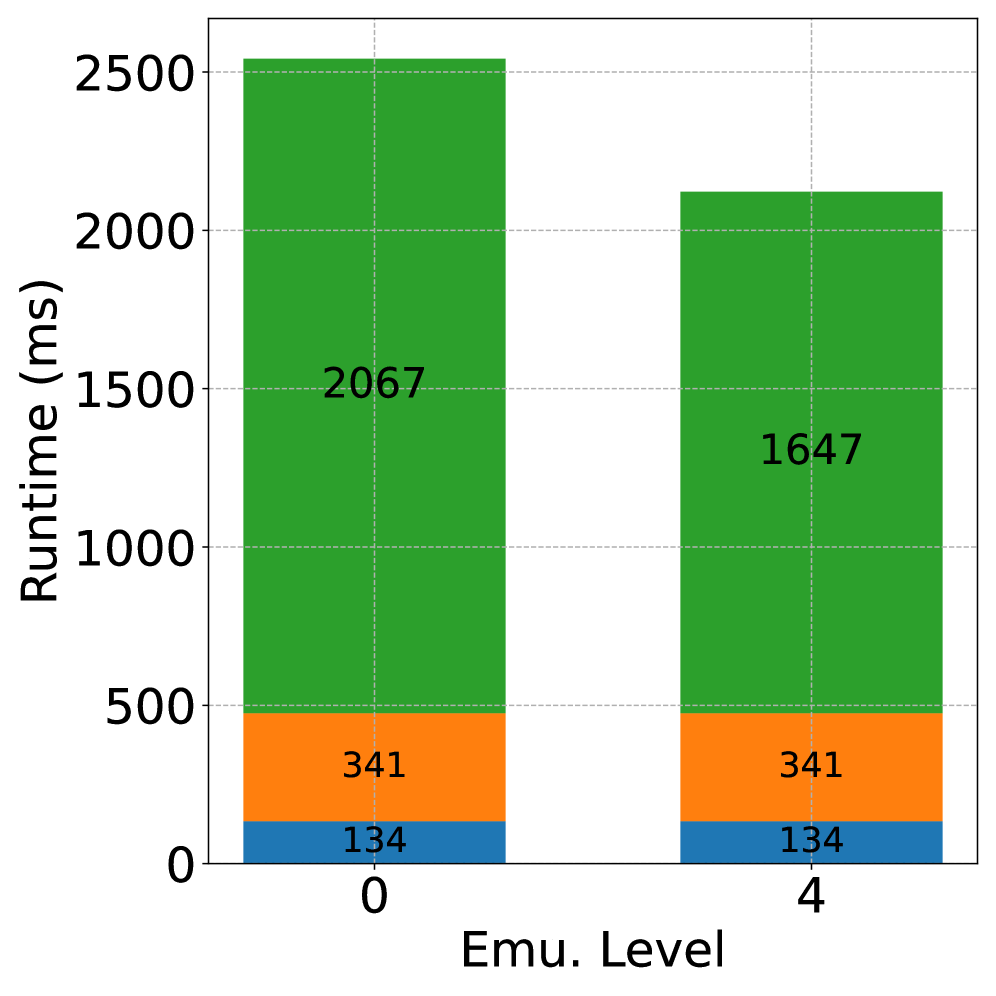
Алгоритмы смешанной точности позволяют снизить вычислительные затраты за счет использования арифметики пониженной точности, например, INT8, когда это целесообразно. Переход от операций с плавающей точкой (FP32 или FP16) к целочисленным операциям INT8 снижает требования к пропускной способности памяти и вычислительной мощности. Однако, важно отметить, что снижение точности может привести к потере значимости и ошибкам округления, поэтому необходимо тщательно анализировать влияние на общую точность результата и использовать методы, такие как масштабирование и накопление, для минимизации этих эффектов. Эффективность применения INT8 зависит от конкретной задачи и архитектуры оборудования, но при грамотной реализации позволяет добиться существенного ускорения вычислений.
Выполнение GEMM (General Matrix Multiplication) с использованием 8-битных целых чисел (INT8) обеспечивает значительное ускорение вычислений, особенно при использовании специализированных аппаратных ускорителей, таких как Tensor Cores. Однако, переход к INT8 требует тщательного анализа численной устойчивости, поскольку снижение разрядности может привести к потере точности и накоплению ошибок округления. Для минимизации этих рисков применяются техники, такие как масштабирование и квантизация, которые позволяют сохранить приемлемый уровень точности при использовании низкоточных вычислений. Ускорение, достигаемое за счет использования INT8 GEMM с Tensor Cores, может превышать 2-3 раза по сравнению с вычислениями в одинарной точности (FP32), что критически важно для задач глубокого обучения и высокопроизводительных вычислений.
Для эффективной реализации INT8 GEMM разработаны специализированные библиотеки, такие как OzIMMU и GEMMul8, оптимизированные для выполнения целочисленных матричных умножений. Помимо них, библиотека cuBLAS обеспечивает поддержку как вычислений с двойной точностью (FP64), так и с использованием INT8, что позволяет добиться значительного повышения производительности при использовании соответствующих аппаратных ускорителей, например, Tensor Cores. Выбор между FP64 и INT8 в cuBLAS позволяет гибко настроить баланс между точностью и скоростью вычислений в зависимости от требований конкретной задачи.
PySCF: Платформа для Эффективной Квантовой Химии
Платформа PySCF, разработанная на языке Python, эффективно объединяет методы Плотного Приближения и Алгоритмы Адаптивной Точности для существенного ускорения квантово-химических расчетов. Плотное Приближение позволяет сократить вычислительные затраты на вычисление двухэлектронных интегралов, заменяя сложные кулоновские взаимодействия более компактным представлением. В свою очередь, адаптивная точность динамически регулирует число значащих цифр в процессе вычислений, обеспечивая необходимую точность результатов при минимальных затратах ресурсов. Такая комбинация позволяет PySCF решать сложные задачи, связанные с моделированием молекулярных систем, значительно быстрее, чем традиционные подходы, открывая новые возможности для исследований в материаловедении и разработке лекарственных препаратов.
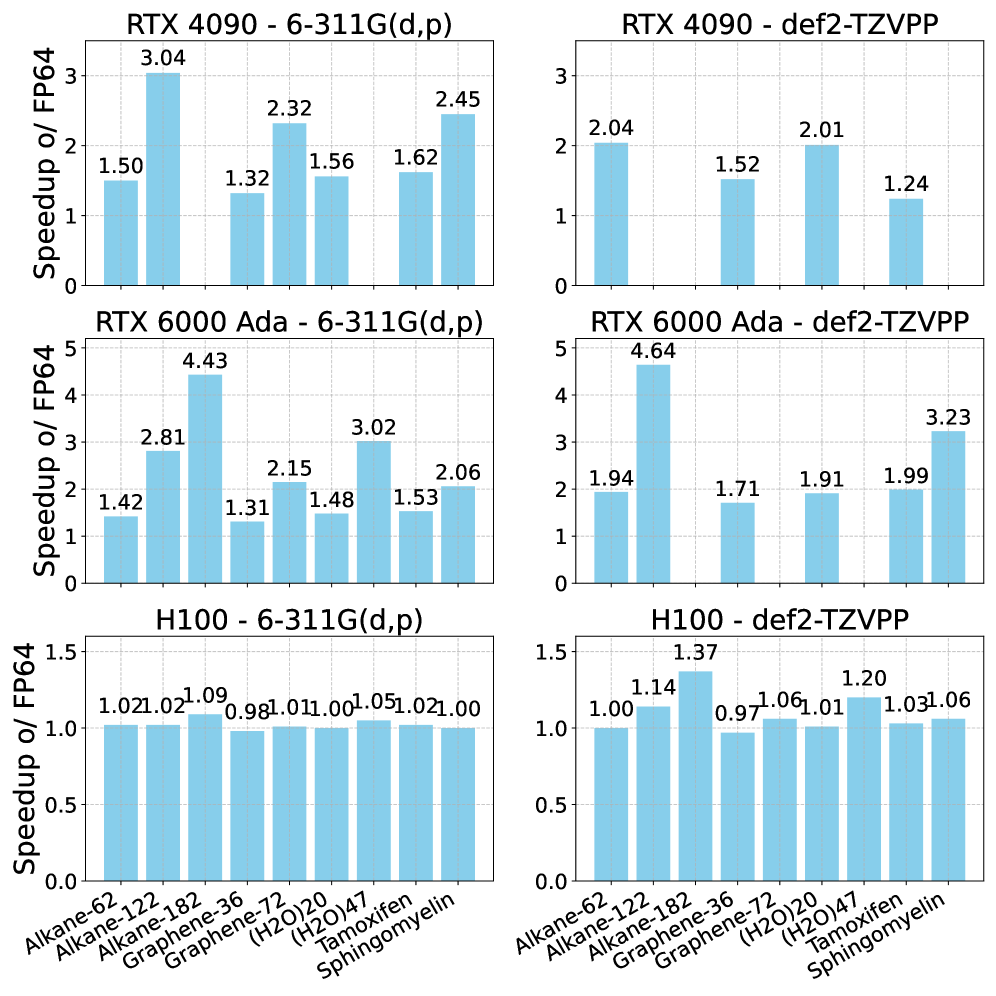
Платформа PySCF демонстрирует существенное увеличение скорости вычислений благодаря использованию целочисленной арифметики INT8 GEMM и аппаратной акселерации. В частности, оптимизация оценки интегралов электронного взаимодействия позволяет достичь прироста производительности до 364% при выполнении полных DFT-расчетов на графическом процессоре NVIDIA RTX 6000 Ada. Такой подход значительно снижает вычислительные затраты, что особенно важно при моделировании крупных и сложных молекулярных систем, открывая новые возможности для исследований в материаловедении и разработке лекарственных препаратов. В результате, PySCF предоставляет эффективный инструмент для проведения высокоточных квантово-химических расчетов с использованием современных аппаратных средств.
Платформа PySCF демонстрирует существенное увеличение скорости вычислений на современных графических процессорах NVIDIA. В частности, на видеокарте RTX 4090 зафиксировано ускорение в 304%, а на NVIDIA H100 — 37%. Данные улучшения позволяют проводить моделирование значительно более крупных и сложных молекулярных систем, что открывает новые возможности для исследований в материаловедении и разработке лекарственных препаратов. Благодаря оптимизации алгоритмов и эффективному использованию аппаратных ресурсов, PySCF способствует более глубокому пониманию свойств материалов и ускоряет процесс открытия новых соединений с заданными характеристиками. Это особенно важно для моделирования сложных химических реакций и изучения взаимодействий между молекулами на атомном уровне.
Представленное исследование демонстрирует стремление к оптимизации вычислительных процессов в квантовой химии посредством адаптивной точности и использования целочисленной арифметики. Подход, описанный в статье, направлен на повышение эффективности вычислений плотности, что критически важно для моделирования сложных молекулярных систем. В этом контексте, слова Николы Теслы: «Я не изобретаю, я открываю то, что уже существует», кажутся особенно уместными. Подобно Тесле, авторы данной работы не создают принципиально новые алгоритмы, а обнаруживают и используют возможности существующих аппаратных средств — Tensor Cores — для решения конкретной научной задачи, значительно ускоряя процесс вычисления плотности и обеспечивая сохранение необходимой точности результатов.
Что дальше?
Представленные результаты, безусловно, демонстрируют потенциал использования целочисленной арифметики и адаптивной точности для ускорения вычислений плотности в квантовой химии. Однако, следует помнить: ускорение — это не абсолютная истина, а лишь относительное снижение времени, измеренное на конкретном аппаратном обеспечении. Вполне вероятно, что дальнейшая оптимизация алгоритмов и аппаратных средств позволит получить ещё более значительные выигрыши, но необходимо учитывать, что каждая оптимизация вносит свой собственный вклад в сложность и потенциальные ошибки. Данные — это не правда, это выборка, и необходимо тщательно анализировать влияние снижения точности на конечный результат.
Необходимо признать, что универсального решения не существует. Эффективность предложенного подхода будет зависеть от множества факторов, включая размер системы, свойства молекул и характеристики используемого AI-ускорителя. В частности, остаются открытыми вопросы о масштабируемости предложенного метода для очень больших систем и о его применимости к другим методам квантово-химических расчётов. Более того, следует учитывать, что адаптивная точность требует тщательной калибровки и валидации, чтобы избежать нежелательных артефактов.
Будущие исследования, вероятно, будут сосредоточены на разработке более интеллектуальных алгоритмов адаптивной точности, которые могут автоматически определять оптимальный уровень точности для каждого конкретного вычисления. Не исключено, что использование методов машинного обучения для предсказания ошибок, возникающих при снижении точности, может стать перспективным направлением. Мы не анализируем реальность — мы аппроксимируем её удобным способом, и важно помнить об этом, продолжая исследования в этой области.
Оригинал статьи: https://arxiv.org/pdf/2601.08077.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Статья также опубликована на личном сайте автора.